作者丨Lovely Zeng

學校丨CUHK

研究方向丨Detection

引言

物體檢測的方法主要分為單階段與兩階段兩大類。雖然兩階段的物體檢測器在準確率上的表現往往更優，但單階段檢測器因其簡潔的結構和相對更快的速度同樣得到了研究者們的重視。

在 2017 年，Focal Loss 的作者指出了單階段檢測器中樣本類別（前景與背景）嚴重不均衡（class imbalance）的問題，並透過設計一個新的損失函式來抑制大量的簡單背景樣本對模型訓練的影響，從而改善了訓練效果。

而在這篇論文中，研究者對樣本不均衡的本質影響進行了進一步探討，找到了梯度分佈這個更為深入的角度，並以此入手改進了單階段檢測器的訓練過程。 

實際上，不同類別樣本數不同並不是影響單階段檢測器的訓練的本質問題，因為背景樣本雖然大部分非常容易識別（well classified），但其中也會存在著比較像某類物體的難樣本（hard negative），而前景類中也有許多網路很容易正確判斷的樣本（easy positive）。所以產生本質影響的問題是不同難度樣本的分佈不均衡。

更進一步來看，每個樣本對模型訓練的實質作用是產生一個梯度用以更新模型的引數，不同樣本對引數更新會產生不同的貢獻。

在單階段檢測器的訓練中，簡單樣本的數量非常大，它們產生的累計貢獻就在模型更新中就會有巨大的影響力甚至佔據主導作用，而由於它們本身已經被模型很好的判別，所以這部分的引數更新並不會改善模型的判斷能力，也就使整個訓練變得低效。

基於這一點，研究者對樣本梯度的分佈進行了統計，並根據這個分佈設計了一個梯度均衡機制（Gradient Harmonizing mechanism），使得模型訓練更加高效與穩健，並可以收斂到更好的結果（實驗中取得了好於 Focal Loss 的表現）。

梯度均衡機制

首先我們要定義統計物件——梯度模長（gradient norm）。考慮簡單的二分類交叉熵損失函式（binary cross entropy loss）：

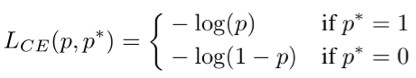
其中 p=sigmoid(x) 為模型所預測的樣本類別的機率，p* 是對應的監督。則其對 x 的梯度（導數）為：

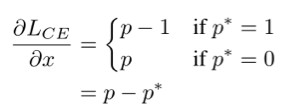
於是我們可以定義一個梯度模長，g=|p-p*|。

對一個交叉熵損失函式訓練收斂的單階段檢測模型，樣本梯度模長的分佈統計如下圖：

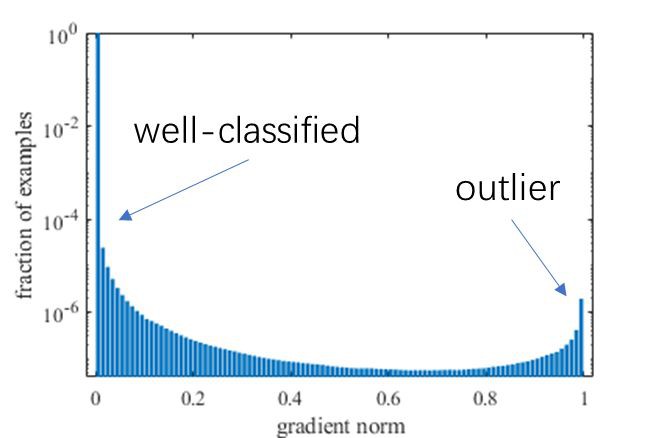
可以看到，絕大多數樣本都是十分容易預測的（well-classified），這些可以被準確預測的樣本所佔的比重非常大，正因如此圖中採用對數坐標來更清楚地展示分佈。

此外，還可以發現在 g 接近 1 的時候，樣本比例也相對較大，研究者認為這是一些離群樣本（outlier），可能是由於資料標註本身不夠準確或是樣本比較特殊極難學習而造成的。對一個已收斂的模型來說，強行學好這些離群樣本可能會導致模型引數的較大偏差，反而會影響大多數已經可以較好識別的樣本的判斷準確率。

基於以上現象與分析，研究者提出了梯度均衡機制，即根據樣本梯度模長分佈的比例，進行一個相應的標準化（normalization），使得各種型別的樣本對模型引數更新有更均衡的貢獻，進而讓模型訓練更加高效可靠。

由於梯度均衡本質上是對不同樣本產生的梯度進行一個加權，進而改變它們的貢獻量，而這個權重加在損失函式上也可以達到同樣的效果，此研究中，梯度均衡機制便是透過重構損失函式來實現的。

為了清楚地描述新的損失函式，我們需要先定義梯度密度（gradient density）這一概念。仿照物理上對於密度的定義（單位體積內的質量），我們把梯度密度定義為單位取值區域內分佈的樣本數量。

具體來說，我們將梯度模長的取值範圍劃分為若干個單位區域（unit region）。對於一個樣本，若它的梯度模長為 g，它的密度就定義為處於它所在的單位區域內的樣本數量除以這個單位區域的長度 ε：

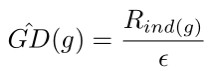
而梯度密度的倒數就是樣本計算 loss 後要乘的權值：

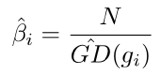
這裡乘樣本數量 N，是為了保證均勻分佈或只劃分一個單位區域時，該權值為 1，即 loss 不變。 

由於這個損失函式是為分類設計的，所以記為 GHM-C Loss。下麵我們透過與傳統交叉熵算是函式以及 Focal Loss 的比較，來進一步解釋 GHM 的作用：

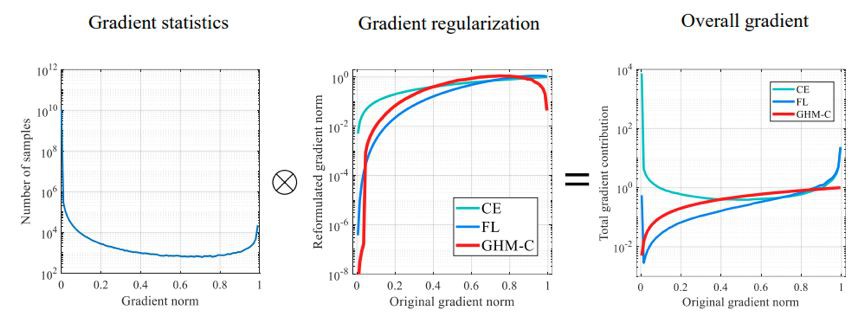
左圖為樣本梯度模長的分佈。中圖為不同損失函式對樣本梯度產生的作用，橫坐標為在交叉熵（CE）損失函式下樣本的梯度模長，縱坐標為新的損失函式下同樣的樣本新的梯度模長，由於範圍較大所以依然採用對數坐標展示。其中淺藍色的線為交叉熵函式本身，作為參考線。

可以看到，Focal Loss 本質上是對簡單樣本進行相對的抑制，越簡單的樣本受抑制的程度越大，這一點和 GHM-C 所做的均衡是十分相似的。此外，GHM-C 還對一些離群樣本進行了相對的抑制，這可以使得模型訓練更具穩定性。

右圖為不同損失函式下，各種難度樣本的累計貢獻大小。由此可以看出，梯度均衡機制的作用就是讓各種難度型別的樣本有均衡的累計貢獻。

在分類之外，研究者還對於候選框的回歸問題做了類似的統計並設計了相應的 GHM-R Loss。

需要指出的是，由於常用的 Smooth L1 Loss 是個分段函式，在 L1 的這部分倒數的模長恆定為 1，也就是偏差超過臨界值的樣本都會落到 g=1 這一點上，沒有難度的區分，這樣的統計並不合理。為瞭解決這個問題，研究者引入了 ASL1 Loss：

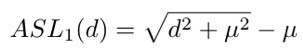
在此基礎上對梯度模長的分佈進行統計並實施均衡化的操作。

實驗結果

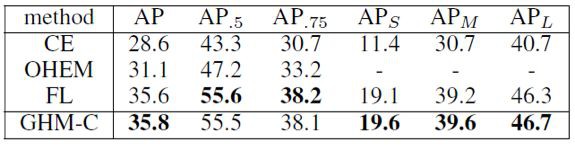
在 COCO 的 minival 集上，GHM-C Loss 與標準 Cross Entropy Loss，使用 OHEM 取樣下 Cross Entropy，以及 Focal Loss 的比較如下：

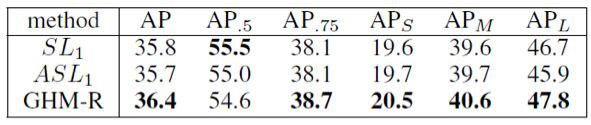
GHM-R 與 Smooth L1 Loss 以及 ASL1 Loss 的 baseline 比較如下：

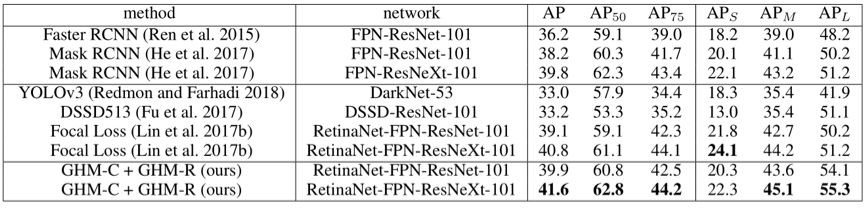
在 COCO test 集上，GHM 與其他 state-of-the-art 的方法比較如下：

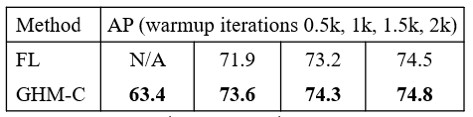
此外，在 AAAI 2019 的簡報中，研究者還展示了在 pascal voc 2007 這樣的小資料集上，GHM 相對於 Focal Loss 不需要過多的 warmup iteration 就可以保持訓練的穩定：

討論

這篇研究的主要貢獻是提供了一個新視角，較為深入地探討了單階段檢測中樣本分佈不均衡所產生的影響及解決方案。

此研究對梯度模長的分佈進行統計並劃分單位區域的方式，實際上可以看作是依據梯度貢獻大小對樣本進行聚類的過程。而這裡的梯度只是模型頂部獲得的偏導數的大小，並不是全部引數對應的梯度向量，所以聚類依據可能有更嚴謹更有區分度的選取方式，然而統計整體引數的梯度分佈會極大增加計算量，所以本研究中的統計方式仍是一種快速且有效的選擇。

此研究進行均衡化操作實際上是以各梯度模長的樣本產生均勻的累計貢獻為標的的，但是這個標的是否就是最優的梯度分佈，暫時無法給出理論上的證明。從實驗結果上，我們可以認為這個標的是明顯優於無均衡的分佈的。然而研究者認為，真正的最優分佈難以定義，並需要後續的深入研究。