(點選上方公眾號,可快速關註)
轉自:heaad
http://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html
遺傳演演算法 ( GA , Genetic Algorithm ) ,也稱進化演演算法 。
遺傳演演算法是受達爾文的進化論的啟發,借鑒生物進化過程而提出的一種啟髮式搜尋演演算法。因此在介紹遺傳演演算法前有必要簡單的介紹生物進化知識。
進化論知識
作為遺傳演演算法生物背景的介紹,下麵內容瞭解即可:
1、種群(Population):生物的進化以群體的形式進行,這樣的一個群體稱為種群。
2、個體:組成種群的單個生物。
3、基因 ( Gene ) :一個遺傳因子。
4、染色體 ( Chromosome ) :包含一組的基因。
5、生存競爭,適者生存:對環境適應度高的、牛B的個體參與繁殖的機會比較多,後代就會越來越多。適應度低的個體參與繁殖的機會比較少,後代就會越來越少。
6、遺傳與變異:新個體會遺傳父母雙方各一部分的基因,同時有一定的機率發生基因變異。
簡單說來就是:繁殖過程,會發生基因交叉( Crossover ) ,基因突變 ( Mutation ) ,適應度( Fitness )低的個體會被逐步淘汰,而適應度高的個體會越來越多。
那麼經過N代的自然選擇後,儲存下來的個體都是適應度很高的,其中很可能包含史上產生的適應度最高的那個個體。
遺傳演演算法思想
借鑒生物進化論,遺傳演演算法將要解決的問題模擬成一個生物進化的過程,透過複製、交叉、突變等操作產生下一代的解,並逐步淘汰掉適應度函式值低的解,增加適應度函式值高的解。
這樣進化N代後就很有可能會進化出適應度函式值很高的個體。
舉個例子,使用遺傳演演算法解決“0-1揹包問題”的思路:0-1揹包的解可以編碼為一串0-1字串(0:不取,1:取) ;首先,隨機產生M個0-1字串,然後評價這些0-1字串作為0-1揹包問題的解的優劣;
然後,隨機選擇一些字串透過交叉、突變等操作產生下一代的M個字串,而且較優的解被選中的機率要比較高。這樣經過G代的進化後就可能會產生出0-1揹包問題的一個“近似最優解”。
編碼
需要將問題的解編碼成字串的形式才能使用遺傳演演算法。最簡單的一種編碼方式是二進位制編碼,即將問題的解編碼成二進位制位陣列的形式。例如,問題的解是整數,那麼可以將其編碼成二進位制位陣列的形式。將0-1字串作為0-1揹包問題的解就屬於二進位制編碼。
遺傳演演算法有3個最基本的操作:選擇,交叉,變異。
選擇
選擇一些染色體來產生下一代。一種常用的選擇策略是 “比例選擇”,也就是個體被選中的機率與其適應度函式值成正比。
假設群體的個體總數是M,那麼那麼一個體Xi被選中的機率為f(Xi)/( f(X1) + f(X2) + …….. + f(Xn) ) 。
比例選擇實現演演算法就是所謂的“輪盤賭演演算法”( Roulette Wheel Selection ) ,輪盤賭演演算法的一個簡單的實現如下:
輪盤賭演演算法
/*
* 按設定的機率,隨機選中一個個體
* P[i]表示第i個個體被選中的機率
*/
int RWS()
{
m =0;
r =Random(0,1); //r為0至1的隨機數
for(i=1;i<=N; i++)
{
/* 產生的隨機數在m~m+P[i]間則認為選中了i
* 因此i被選中的機率是P[i]
*/
m = m + P[i];
if(r<=m) return i;
}
}
交叉(Crossover)
2條染色體交換部分基因,來構造下一代的2條新的染色體。
例如:
交叉前:
00000|011100000000|10000
11100|000001111110|00101
交叉後:
00000|000001111110|10000
11100|011100000000|00101
染色體交叉是以一定的機率發生的,這個機率記為Pc 。
變異(Mutation):在繁殖過程,新產生的染色體中的基因會以一定的機率出錯,稱為變異。變異發生的機率記為Pm 。例如:
變異前:
000001110000000010000
變異後:
000001110000100010000
適應度函式 ( Fitness Function ):用於評價某個染色體的適應度,用f(x)表示。有時需要區分染色體的適應度函式與問題的標的函式。
例如:0-1揹包問題的標的函式是所取得物品價值,但將物品價值作為染色體的適應度函式可能並不一定適合。適應度函式與標的函式是正相關的,可對標的函式作一些變形來得到適應度函式。
基本遺傳演演算法的偽程式碼
基本遺傳演演算法偽程式碼
/*
* Pc:交叉發生的機率
* Pm:變異發生的機率
* M:種群規模
* G:終止進化的代數
* Tf:進化產生的任何一個個體的適應度函式超過Tf,則可以終止進化過程
*/
初始化Pm,Pc,M,G,Tf等引數。隨機產生第一代種群Pop
do
{
計算種群Pop中每一個體的適應度F(i)。
初始化空種群newPop
do
{
根據適應度以比例選擇演演算法從種群Pop中選出2個個體
if ( random ( 0 , 1 ) < Pc )
{
對2個個體按交叉機率Pc執行交叉操作
}
if ( random ( 0 , 1 ) < Pm )
{
對2個個體按變異機率Pm執行變異操作
}
將2個新個體加入種群newPop中
} until ( M個子代被建立 )
用newPop取代Pop
}until ( 任何染色體得分超過Tf, 或繁殖代數超過G )
基本遺傳演演算法最佳化
下麵的方法可最佳化遺傳演演算法的效能。
精英主義(Elitist Strategy)選擇:是基本遺傳演演算法的一種最佳化。為了防止進化過程中產生的最優解被交叉和變異所破壞,可以將每一代中的最優解原封不動的複製到下一代中。
插入操作:可在3個基本操作的基礎上增加一個插入操作。插入操作將染色體中的某個隨機的片段移位到另一個隨機的位置。
使用AForge.Genetic解決TSP問題
AForge.NET是一個C#實現的面向人工智慧、計算機視覺等領域的開源架構。
AForge.NET中包含有一個遺傳演演算法的類庫。
AForge.NET主頁:http://www.aforgenet.com/
AForge.NET程式碼下載:http://code.google.com/p/aforge/
介紹一下AForge的遺傳演演算法用法吧。AForge.Genetic的類結構如下:
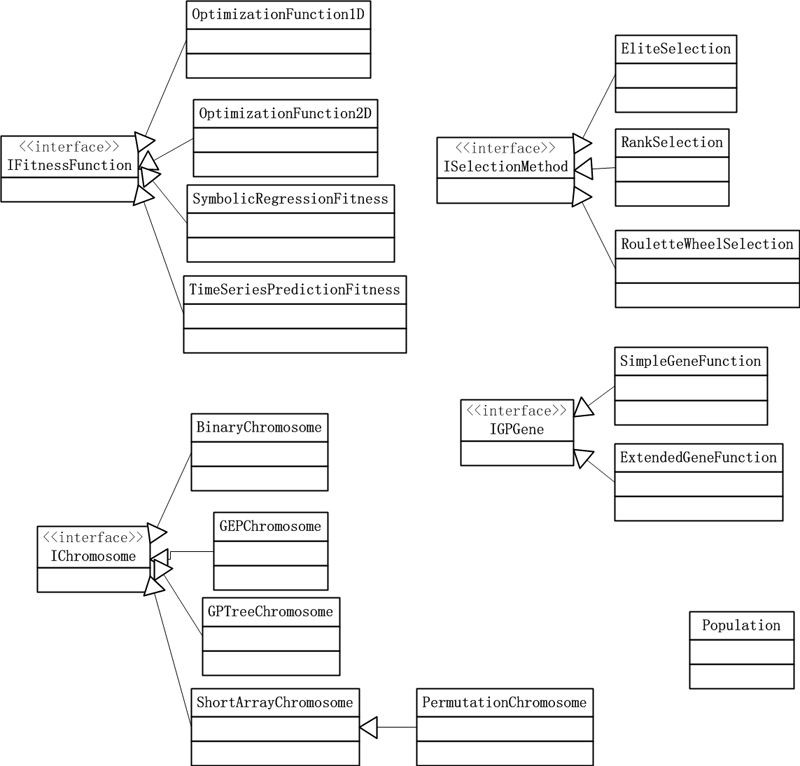
圖1. AForge.Genetic的類圖
下麵用AForge.Genetic寫個解決TSP問題的最簡單實體。測試資料集採用網上流傳的中國31個省會城市的坐標:
36391315
37121399
33261556
41961004
4386570
25621756
23811676
37151678
40612370
36762578
42632931
35072367
34393201
31403550
27782826
操作過程
(1) 下載AForge.NET類庫,網址:http://code.google.com/p/aforge/downloads/list
(2) 建立C#空專案GenticTSP。然後在AForge目錄下找到AForge.dll和AForge.Genetic.dll,將其複製到TestTSP專案的bin/Debug目錄下。再透過“Add Reference…”將這兩個DLL新增到工程。
(3) 將31個城市坐標資料儲存為bin/Debug/Data.txt 。
(4) 新增TSPFitnessFunction.cs,加入如下程式碼:
TSPFitnessFunction類
using System;
using AForge.Genetic;
namespace GenticTSP
{
///
/// Fitness function for TSP task (Travaling Salasman Problem)
///
publicclass TSPFitnessFunction : IFitnessFunction
{
// map
privateint[,] map =null;
// Constructor
public TSPFitnessFunction(int[,] map)
{
this.map = map;
}
///
/// Evaluate chromosome – calculates its fitness value
///
publicdouble Evaluate(IChromosome chromosome)
{
return1/ (PathLength(chromosome) +1);
}
///
/// Translate genotype to phenotype
///
publicobject Translate(IChromosome chromosome)
{
return chromosome.ToString();
}
///
/// Calculate path length represented by the specified chromosome
///
publicdouble PathLength(IChromosome chromosome)
{
// salesman path
ushort[] path = ((PermutationChromosome)chromosome).Value;
// check path size
if (path.Length != map.GetLength(0))
{
thrownew ArgumentException(“Invalid path specified – not all cities are visited”);
}
// path length
int prev = path[0];
int curr = path[path.Length –1];
// calculate distance between the last and the first city
double dx = map[curr, 0] – map[prev, 0];
double dy = map[curr, 1] – map[prev, 1];
double pathLength = Math.Sqrt(dx * dx + dy * dy);
// calculate the path length from the first city to the last
for (int i =1, n = path.Length; i < n; i++)
{
// get current city
curr = path[i];
// calculate distance
dx = map[curr, 0] – map[prev, 0];
dy = map[curr, 1] – map[prev, 1];
pathLength += Math.Sqrt(dx * dx + dy * dy);
// put current city as previous
prev = curr;
}
return pathLength;
}
}
}
(5) 新增GenticTSP.cs,加入如下程式碼:
GenticTSP類
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.IO;
using AForge;
using AForge.Genetic;
namespace GenticTSP
{
class GenticTSP
{
staticvoid Main()
{
StreamReader reader =new StreamReader(“Data.txt”);
int citiesCount =31; //城市數
int[,] map =newint[citiesCount, 2];
for (int i =0; i < citiesCount; i++)
{
string value = reader.ReadLine();
string[] temp = value.Split(”);
map[i, 0] =int.Parse(temp[0]); //讀取城市坐標
map[i, 1] =int.Parse(temp[1]);
}
// create fitness function
TSPFitnessFunction fitnessFunction =new TSPFitnessFunction(map);
int populationSize = 1000; //種群最大規模
/*
* 0:EliteSelection演演算法
* 1:RankSelection演演算法
* 其他:RouletteWheelSelection 演演算法
* */
int selectionMethod =0;
// create population
Population population =new Population(populationSize,
new PermutationChromosome(citiesCount),
fitnessFunction,
(selectionMethod ==0) ? (ISelectionMethod)new EliteSelection() :
(selectionMethod ==1) ? (ISelectionMethod)new RankSelection() :
(ISelectionMethod)new RouletteWheelSelection()
);
// iterations
int iter =1;
int iterations =5000; //迭代最大週期
// loop
while (iter < iterations)
{
// run one epoch of genetic algorithm
population.RunEpoch();
// increase current iteration
iter++;
}
System.Console.WriteLine(“遍歷路徑是: {0}”, ((PermutationChromosome)population.BestChromosome).ToString());
System.Console.WriteLine(“總路程是:{0}”, fitnessFunction.PathLength(population.BestChromosome));
System.Console.Read();
}
}
}
網上據稱這組TSP資料的最好的結果是 15404 ,上面的程式我剛才試了幾次最好一次算出了15402.341,但是最差的時候也跑出了大於16000的結果。
我這還有一個版本,設定種群規模為1000,迭代5000次可以算出15408.508這個結果。原始碼在文章最後可以下載。
總結一下使用AForge.Genetic解決問題的一般步驟:
(1) 定義適應函式類,需要實現IFitnessFunction介面
(2) 選定種群規模、使用的選擇演演算法、染色體種類等引數,建立種群population
(3)設定迭代的最大次數,使用RunEpoch開始計算
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」,修煉程式設計內功
 知識星球
知識星球