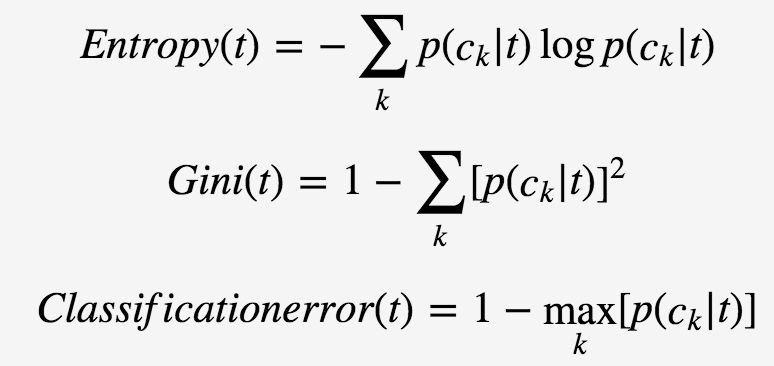
其中，p(ck|t)表示對於決策樹節點tt類別ckck的機率。這三種不純度的度量是等價的，在等機率分佈是達到最大值。

為了判斷分裂前後節點不純度的變化情況，標的函式定義為資訊增益（information gain）：

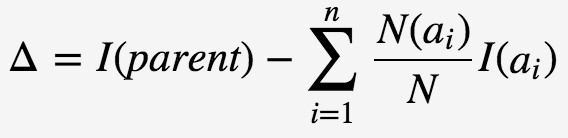
I(⋅)對應於決策樹節點的不純度，parent表示分裂前的父節點，N表示父節點所包含的樣本記錄數，ai表示父節點分裂後的某子節點，N(ai)為其計數，n為分裂後的子節點數。

特別地，ID3演演算法選取熵值作為不純度I(⋅)的度量，則

c指父節點對應所有樣本記錄的類別；A表示選擇的特徵屬性，即ai的集合。那麼，決策樹學習中的資訊增益Δ等價於訓練資料集中類與特徵的互資訊，表示由於得知特徵A的資訊訓練資料集c不確定性減少的程度。

在特徵分裂後，有些子節點的記錄數可能偏少，以至於影響分類結果。為瞭解決這個問題，CART演演算法提出了只進行特徵的二元分裂，即決策樹是一棵二叉樹；C4.5演演算法改進分裂標的函式，用資訊增益比（information gain ratio）來選擇特徵：

因而，特徵選擇的過程等同於計算每個特徵的資訊增益，選擇最大資訊增益的特徵進行分裂。

此即回答前面所提出的第一個問題（選擇較優特徵）。ID3演演算法設定一閾值，當最大資訊增益小於閾值時，認為沒有找到有較優分類能力的特徵，沒有往下繼續分裂的必要。

根據最大表決原則，將最多計數的類別作為此葉子節點。即回答前面所提出的第二個問題（停止分裂條件）。

決策樹生成

ID3演演算法的核心是根據資訊增益最大的準則，遞迴地構造決策樹；演演算法流程如下：

1、如果節點滿足停止分裂條件（所有記錄屬同一類別 or 最大資訊增益小於閾值），將其置為葉子節點；

2、選擇資訊增益最大的特徵進行分裂；

3、重覆步驟1-2，直至分類完成。

C4.5演演算法流程與ID3相類似，只不過將資訊增益改為資訊增益比。

決策樹剪枝

過擬合

生成的決策樹對訓練資料會有很好的分類效果，卻可能對未知資料的預測不準確，即決策樹模型發生過擬合（overfitting）——訓練誤差（training error）很小、泛化誤差（generalization error，亦可看作為test error）較大。

下圖給出訓練誤差、測試誤差（test error）隨決策樹節點數的變化情況：

可以觀察到，當節點數較小時，訓練誤差與測試誤差均較大，即發生了欠擬合（underfitting）。

當節點數較大時，訓練誤差較小，測試誤差卻很大，即發生了過擬合。只有當節點數適中是，訓練誤差居中，測試誤差較小；對訓練資料有較好的擬合，同時對未知資料有很好的分類準確率。

發生過擬合的根本原因是分類模型過於複雜，可能的原因如下：

1、訓練資料集中有噪音樣本點，對訓練資料擬合的同時也對噪音進行擬合，從而影響了分類的效果；

2、決策樹的葉子節點中缺乏有分類價值的樣本記錄，也就是說此葉子節點應被剪掉。

剪枝策略

如果剪枝後損失函式減少了，即說明這是有效剪枝。具體剪枝演演算法可以由動態規劃等來實現。

參考資料

[1] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.
[2] 李航，《統計學習方法》.
[3] Naren Ramakrishnan, The Top Ten Algorithms in Data Mining

覺得本文有幫助？請分享給更多人

關註「演演算法愛好者」，修煉程式設計內功

‍‍‍‍