（點選上方公眾號，可快速關註）

轉自：BYRans

http://www.cnblogs.com/BYRans/p/4700202.html

好文投稿， 請點選 → 這裡瞭解詳情

實體

    

首先舉個例子，假設我們有一個二手房交易記錄的資料集，已知房屋面積、臥室數量和房屋的交易價格，如下表：

    

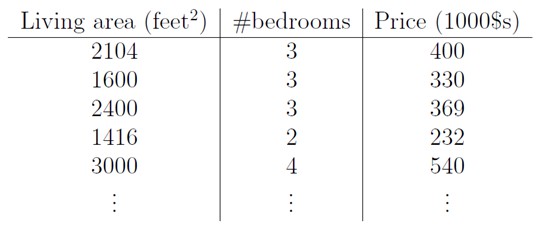
假如有一個房子要賣，我們希望透過上表中的資料估算這個房子的價格。這個問題就是典型的回歸問題，這邊文章主要講回歸中的線性回歸問題。

 

線性回歸（Linear Regression）

    

首先要明白什麼是回歸。回歸的目的是透過幾個已知資料來預測另一個數值型資料的標的值。

假設特徵和結果滿足線性關係，即滿足一個計算公式h(x)，這個公式的自變數就是已知的資料x，函式值h(x)就是要預測的標的值。這一計算公式稱為回歸方程，得到這個方程的過程就稱為回歸。

    

線性回歸就是假設這個方式是一個線性方程，即假設這個方程是一個多元一次方程。

以咱們上面提到的例子為例：假設房子的房屋面積和臥室數量為自變數x，用x1表示房屋面積，x2表示臥室數量；房屋的交易價格為因變數y，我們用h(x)來表示y。假設房屋面積、臥室數量與房屋的交易價格是線性關係。

他們滿足公式

    

    

上述公式中的θ為引數，也稱為權重，可以理解為x1和x2對h(x)的影響度。對這個公式稍作變化就是

    

    

公式中θ和x是向量，n是樣本數。

    

假如我們依據這個公式來預測h(x)，公式中的x是我們已知的，然而θ的取值卻不知道，只要我們把θ的取值求解出來，我們就可以依據這個公式來做預測了。

    

那麼如何依據訓練資料求解θ的最優取值呢？這就牽扯到另外一個概念：損失函式（Loss Function）。

 

損失函式（Loss Function）

    

我們要做的是依據我們的訓練集，選取最優的θ，在我們的訓練集中讓h(x)盡可能接近真實的值。

h(x)和真實的值之間的差距，我們定義了一個函式來描述這個差距，這個函式稱為損失函式，運算式如下：

    

這裡的這個損失函式就是著名的最小二乘損失函式，這裡還涉及一個概念叫最小二乘法，這裡不再展開了。

    

我們要選擇最優的θ，使得h(x)最近進真實值。這個問題就轉化為求解最優的θ，使損失函式J(θ)取最小值。

那麼如何解決這個轉化後的問題呢？這又牽扯到一個概念：梯度下降（Radient Descent）

最小均方演演算法（Least mean square，LMS演演算法）

（對的朋友，你沒有看錯，不是梯度下降，是LMS演演算法。耐心點，梯度下降一會兒就出來了）

我們先來看當訓練樣本只有一個的時候的情況，然後再將訓練樣本擴大到多個的情況。

訓練樣本只有一個的情況，我們借鑒LMS演演算法的思想。擴大到多個我們稍後說。

    

我們要求解使得J(θ)最小的θ值，LMS演演算法大概的思路是：我們首先隨便給θ一個初始化的值，然後改變θ值讓J(θ)的取值變小，不斷重覆改變θ使J(θ)變小的過程直至J(θ)約等於最小值。

    

首先我們給θ一個初試值，然後向著讓J(θ)變化最大的方向更新θ的取值，如此迭代。公式如下：

    

    

公式中α稱為步長（learning rate），它控制θ每次向J(θ)變小的方向迭代時的變化幅度。J(θ)對θ的偏導表示J(θ)變化最大的方向。由於求的是極小值，因此梯度方向是偏導數的反方向。求解一下這個偏導，過程如下：

    

    

那麼θ的迭代公式就變為：

    

    

這是當訓練集只有一個樣本時的數學表達。

我們又兩種方式將只有一個樣本的數學表達轉化為樣本為多個的情況：梯度下降（gradient descent）和正則方程（The normal equations）。

這裡我們重點講梯度下降。

 

梯度下降

批梯度下降（batch gradient descent）

    

如下公式是處理一個樣本的運算式：

    

    

轉化為處理多個樣本就是如下表達：

    

    

這種新的運算式每一步都是計算的全部訓練集的資料，所以稱之為批梯度下降（batch gradient descent）。

    

註意，梯度下降可能得到區域性最優，但在最佳化問題裡我們已經證明線性回歸只有一個最優點，因為損失函式J(θ)是一個二次的凸函式，不會產生區域性最優的情況。（假設學習步長α不是特別大）

    

批梯度下降的演演算法執行過程如下圖：

    

 

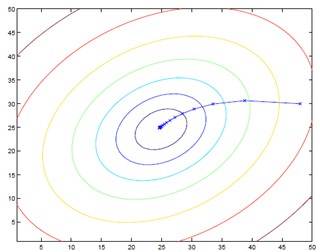
大家仔細看批梯度下降的數學運算式，每次迭代的時候都要對所有資料集樣本計算求和，計算量就會很大，尤其是訓練資料集特別大的情況。那有沒有計算量較小，而且效果也不錯的方法呢？有！這就是：隨機梯度下降（Stochastic Gradient Descent, SGD）

 

隨機梯度下降（Stochastic Gradient Descent, SGD）

    

隨機梯度下降在計算下降最快的方向時時隨機選一個資料進行計算，而不是掃描全部訓練資料集，這樣就加快了迭代速度。

隨機梯度下降並不是沿著J(θ)下降最快的方向收斂，而是震蕩的方式趨向極小點。餘凱教授在龍星計劃課程中用“曲線救國”來比喻隨機梯度下降。

隨機梯度下降運算式如下：

    

    

執行過程如下圖：

    

    

批梯度下降和隨機梯度下降在三維圖上對比如下：

    

 

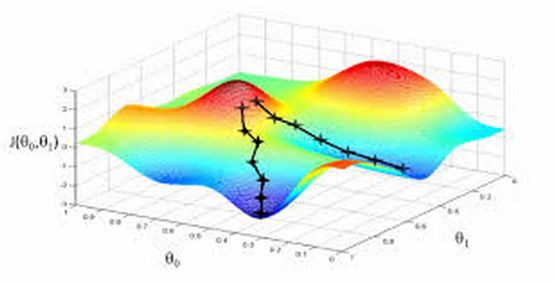
總結

    

線性回歸是回歸問題中的一種，線性回歸假設標的值與特徵之間線性相關，即滿足一個多元一次方程。使用最小二乘法構建損失函式，用梯度下降來求解損失函式最小時的θ值。

覺得本文有幫助？請分享給更多人

關註「演演算法愛好者」，修煉程式設計內功