
授權轉載自大資料文摘 ID:BigDataDigest
作者:Marcin Moskala

關於程式設計工作有很多很不錯的面試謎題。新年之際,我把壓箱底兒的一道好題,同時也是傳說中谷歌招聘官最喜歡問的一道題找出來了!
今天我們來好好八一八這道題,如果你今年恰好想去谷歌面試,可以抓緊多讀幾遍!(絕對不會出現下圖的情況,我們只放有口碑的神助攻![]() )
)

題目如下:
你在一座100層的高樓大廈裡工作,拿到了兩個一模一樣的雞蛋。你得搞明白雞蛋最高可以從幾層樓扔出去還不摔壞。
請提出一個演演算法,能找到投擲雞蛋卻保證不摔壞的最少次數~
我們可以先做些假設:
-
如果雞蛋從某一樓層跌落而不摔壞,那麼當它從更低樓層跌落也不會有破損。
-
一個在被投擲之後完好無損的蛋可以被再利用。
-
一顆雞蛋如果破損,則必會被丟棄。
-
跌落對於所有雞蛋都具有同等效應。
-
如果一顆雞蛋從某一樓層跌落之後受損,那麼當它從更高樓層跌落後必定會摔壞。
-
如果一顆雞蛋從一次跌落中存活下來,那麼它一定會從更短程的降落中存活。
大多數人會寫出演演算法來解決這個謎題(我們同樣也是會用演演算法),然而實際上有更容易的辦法。
敲黑板說重點啦!

01 最簡單的回答
最簡單的方式來獲取最少樓層數就是將雞蛋從第一層扔出,然後第二層,然後依次往後疊加。這樣一來,當雞蛋破碎那一刻我們就知道是這一層了。這是一個可靠的演演算法,但是在最差的情況下它需要的投擲次數是100次。
需要註意的最重要的一點是,假如你只有一顆雞蛋,這是唯一可靠的方法。所以在你打破第一顆雞蛋時就需要開始運用這個演演算法。
02 直覺性的答案
這樣,我們應該把這100層劃分成更小數目的的區間,以盡可能有效地應用這第一顆雞蛋。因此,一個憑直覺的而且頗受歡迎的方法是從1/第n層逐層檢查。
比方說,從第一層到第三層。由此得出演演算法如下:
-
從33樓投擲出這顆雞蛋。如果它破損了,那麼我們用第二顆雞蛋檢查第32層樓。
-
否則,我們從33+ (67 *1/3) =55層樓扔,如果雞蛋破損,我們再來用第二顆雞蛋檢查34層到55層。
-
…
對於1/3最壞的情況是最大值是33層,這樣一來,我們可能可以找到一個完美的n,藉助一些動態程式設計手段,來最佳化投擲次數。這是一個體現程式設計思維的有價值的解決方式,然而這不是最優解。
03 完美解決方案
為了理解完美解法,我們需要理解均衡狀態,用於計算出在最壞情境下所需的投擲次數。

這裡,F(n) 是我們從開始投擲雞蛋計算的下一層樓層。
假如我們引入以下的變數:

那麼均衡點將會是如下:
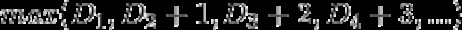
最優解是當這個方程裡的所有引數都相等。我們是如何取得的呢?從末尾開始看,最後的D(n)將會變成1,因為我們最終將會到達一個點,就是隻有單一的一層樓用於投擲第一顆雞蛋。所以D(n-1)應該等於2,因為它相比於第一顆雞蛋少了一次投擲。
我們接著會發現第一顆雞蛋最終應該是從第99層樓投擲,之前是從99-2=97層,再往前則是97-3=94層,90, 85, 79, 72, 64, 55, 45, 34, 22,然後是第九層。這是一個最優解!這樣一來,我們需要在最壞的情況下投擲14次(最小的差別在於13,但是我們還需要在第九層額外投一次)。
04 檢查
好啦,我們已經有瞭解決方案,可以無需任何其他幫助來解開它。現在是時候驗證它是否正確了!為此,我們可以寫一個Kotlin方程式。
首先,我們來解釋一下對一些決策來說,是如何計算投擲次數的。當我們有2層或者更少的層數,那麼我們需要按照剩餘的樓層數來投擲儘量多的次數。否則我們應該呼叫如下方呈現的均衡函式:

這裡我們呼叫了bestMaxThrows 函式,這是一個假設函式,它會傳回一個投擲次數的數值,假定接下來的一系列決策是完美的。
我們是這樣定義它的:

再一次的,我們剛剛授權給了bestNextStep 函式來計算“下一層的最優解”。這個函式很好的為我們指明瞭下一步的方向,我們可以簡單地定義它:當只有二層或更少的樓層待檢驗,那我們會從第一層扔出雞蛋,否則我們需要檢查所有備選項以找到最優解。
下麵是具體執行步驟:

再一次的,我們剛剛授權給了bestNextStep 函式來計算“下一層的最優解”。這個函式很好的為我們指明瞭下一步的方向,我們可以簡單地定義它:當只有二層或更少的樓層待檢驗,那我們會從第一層扔出雞蛋,否則我們需要檢查所有備選項以找到最優解。
下麵是具體執行步驟:

註意,這個函式使用了maxThrows 函式,所以涉及到了迴圈。這不是個問題,因為當bestNextStep 呼叫到maxThrows時,它總是呼叫一個小於floorsLeft 的數(因為nextFloor 總是大於0)。我們呼叫這個函式之前先加一些緩衝,用於加速這些運算。

首先,我們看看它是否傳回和之前計算相同的結果。

結果看著不錯,我們再看看下麵幾步:

結果:
9, 22, 34, 45, 55, 64, 72, 79, 85, 90, 94, 97, 99, 100,
正是我們計算的結果!贊!

05 拓展
現在我們有了一套可以解決很多相似問題的不錯的演演算法。比如說,我們可以稍微修改一下來計算最隨機的情況下的投擲次數。我們也可以看看這一最小數值如何根據建築高度不同而有所區別。
下圖回答了以上的問題:

(該圖展示了最壞情景的最少投擲次數,縱軸是樓層數,橫軸是投擲次數,曲線代表最優投擲次數。)
06 結論
你現在對於谷歌的面試準備更充分了,但更重要的是,你相比以前更具備演演算法思想。這個演演算法呈現了一個很好的,高效型的方法。還可應用於解決我們每日工作中的許多問題。

精彩活動
推薦閱讀
2017年資料視覺化的七大趨勢!
全球100款大資料工具彙總(前50款)
Q: 如果是你,你會如何解答?
歡迎留言與大家分享
請把這篇文章分享給你的朋友
轉載 / 投稿請聯絡:hzzy@hzbook.com
更多精彩文章,請在公眾號後臺點選“歷史文章”檢視

 知識星球
知識星球