作者丨蘇劍林
單位丨廣州火焰資訊科技有限公司
研究方向丨NLP,神經網路
個人主頁丨kexue.fm
2017 年的時候筆者曾寫過互懟的藝術:從零直達WGAN-GP,從一個相對通俗的角度來介紹了 WGAN,在那篇文章中,WGAN 更像是一個天馬行空的結果,而實際上跟 Wasserstein 距離沒有多大關係。
在本篇文章中,我們再從更數學化的視角來討論一下 WGAN。當然,本文並不是純粹地討論 GAN,而主要側重於 Wasserstein 距離及其對偶理論的理解。

▲ 推土機哪家強?成本最低找Wasserstein
本文受啟發於著名的國外博文 Wasserstein GAN and the Kantorovich-Rubinstein Duality [1],內容跟它大體上相同,但是刪除了一些冗餘的部分,對不夠充分或者含糊不清的地方作了補充。不管怎樣,在此先對前輩及前輩的文章表示致敬。
註:完整理解本文,應該需要多元微積分、機率論以及線性代數等基礎知識。還有,本文確實長,數學公式確實多,但是,真的不複雜、不難懂,大家不要看到公式就嚇怕了。
Wasserstein距離
顯然,整篇文章必然圍繞著 Wasserstein 距離(W 距離)來展開。假設我們有了兩個機率分佈 p(x),q(x),那麼 Wasserstein 距離的定義為:
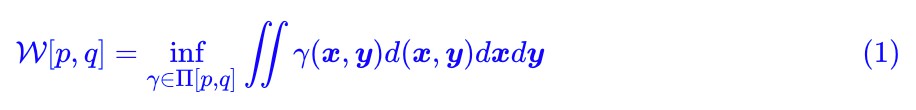
事實上,這也算是最優傳輸理論中最核心的定義了。
相信我,式 (1) 沒有想象中那麼難理解。我們來逐項看看。
成本函式
首先 d(x,y) ,它不一定是距離,其準確含義應該是一個成本函式,代表著從 x 運輸到 y 的成本。常用的 d 是基於 l 範數衍生出來的,比如:
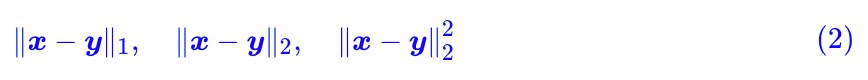
都是常見的選擇,其中:
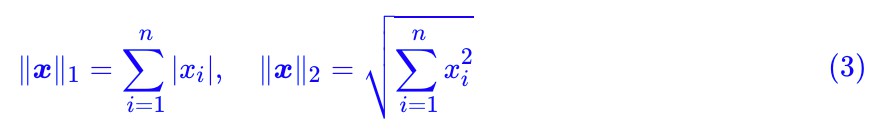
特別指出,其實哪種距離並不是特別重要,因為很多範數都是相互等價的,範數的等價性表明其實最終定義出來的 W 距離都差不多。
成本最小化
然後來看 γ ,條件 γ∈Π[p,q] 意味著:
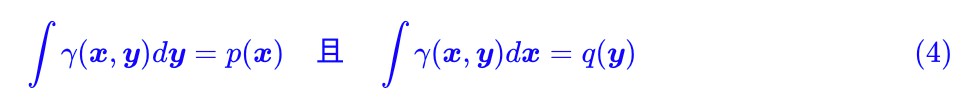
這也就是說, γ 是一個聯合分佈,它的邊緣分佈就是原來的 p 和 q。
事實上 γ 就描述了一種運輸方案。不失一般性,設 p 是原始分佈,設 q 是標的分佈, p(x) 的意思是原來在位置 x 處有 p(x) 量的貨物, q(x) 是指最終 x 處要存放的貨物量,如果 p(x)>q(x) ,那麼就要把 x 處的一部分貨物運到別處,反之,如果 p(x)
最後是 inf ,這表示下確界,簡單來說就是取最小,也就是說,要從所有的運輸方案中,找出總運輸成本 ∬γ(x,y)d(x,y)dxdy 最小的方案,這個方案的成本,就是我們要算的 W[p,q] 。
如果將上述比喻中的“貨物”換成“沙土”,那麼 Wasserstein 距離就是在求最省力的“搬土”方案了,所以 Wasserstein 距離也被稱為“推土機距離”(Earth Mover’s Distance)。
最後改編一張開頭提到的國外博文的圖片,來展示這個“推土”過程:
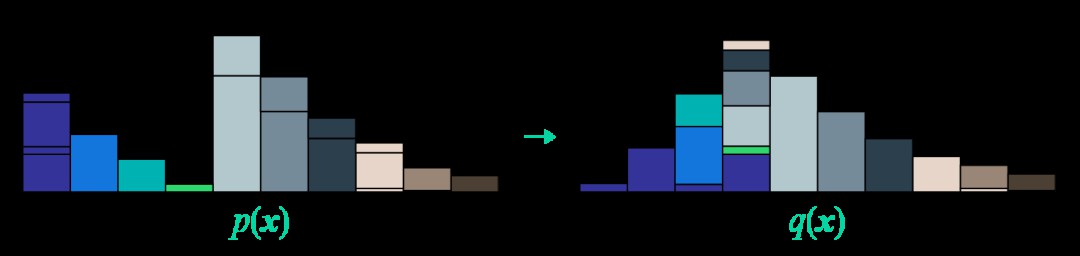
▲ 推土機距離圖示。左邊p(x)每處的沙土被分為若干部分,然後運輸到右端q(x)的同色的位置(或者不動)
矩陣形式
逐項分析完含義之後,現在我們再來完成地重述一下問題,我們實際上在求下式的最小值:

其中 d(x,y) 是事先給定的,而這個最小值要滿足如下約束:
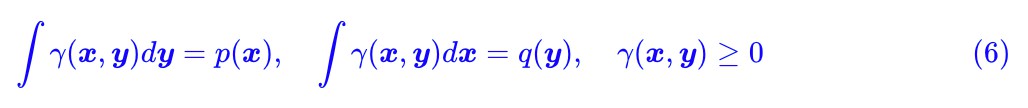
認真盯著式 (5),考慮到積分只是求和的極限形式,所以我們可以把 γ(x,y) 和 d(x,y) 離散化,然後看成很長很長的(列)向量 Γ 和 D:
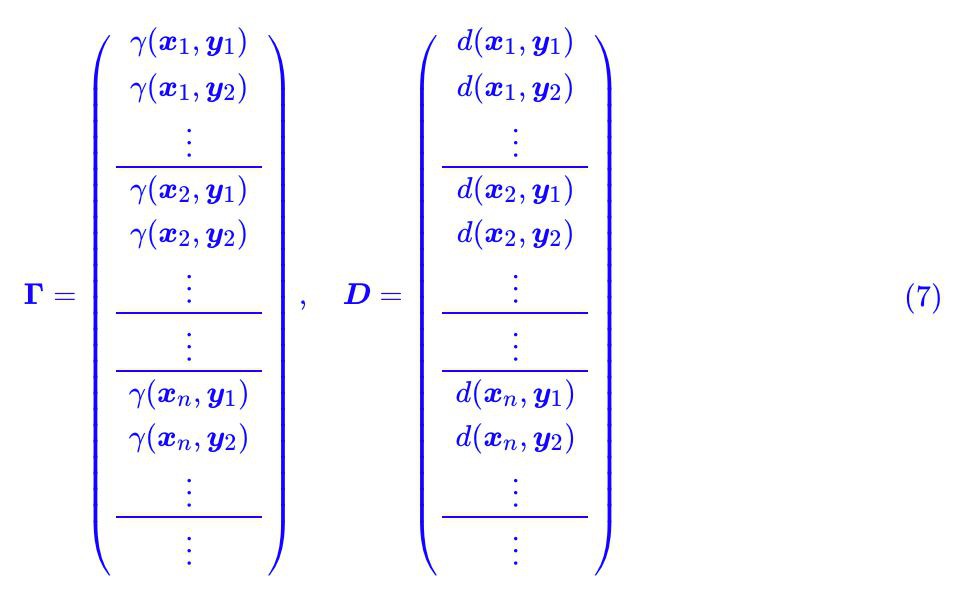
所以式 (5) 相當於就是將 Γ 和 D 對應位置相乘,然後求和,這不就是內積 ⟨Γ,D⟩ 了嗎?
如果還沒理解這一點,那麼請再好好地盯一會式 (5),頭腦中想象著將 x,y 分割槽間離散化的過程,再想想積分的定義,相信這並不難理解。
如果已經理解了這一點,那就好辦了,我們可以把約束條件 (6) 也這樣看:把 p(x),q(x) 分別看成一個長向量,然後還可以拼起來,把積分也看成求和,這時候約束條件 (6) 也可以寫成矩陣形式 AΓ=b:
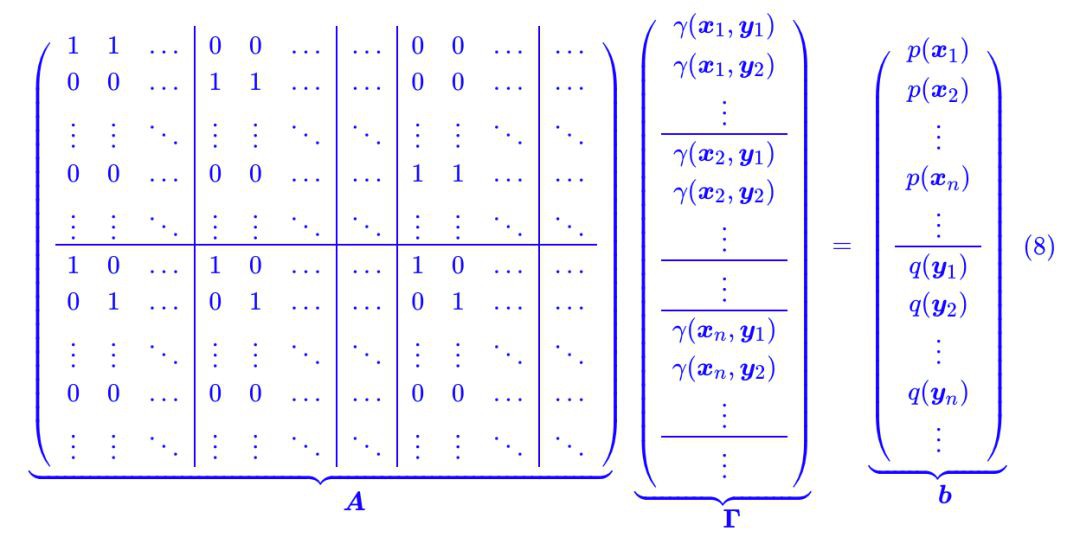
最後不能忘記的是 Γ ≥ 0 ,它表示 Γ 的每個分量都大於等於 0。
線性規劃問題
現在問題可以用一行字來描述:
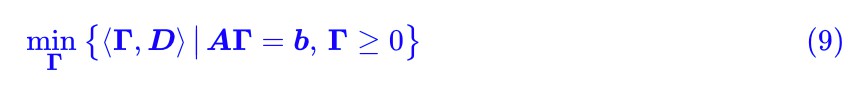
這就是“線性約束下的線性函式最小值”的問題,它就是我們在高中時就已經接觸過的線性規劃問題了。可見,雖然原始問題足夠複雜,又有積分又有下確界的,但經過轉寫,它本質上就是一個並不難理解的線性規劃問題(當然,“不難理解”並不意味著“容易求解”)。
線性規劃與對偶
讓我們用更一般的記號,把線性規劃問題重寫一遍,常見的形式有兩種:

這兩種形式本質上是等價的,只不過在討論第一種的時候相對簡單一點(真的只是簡單一點點,並沒有本質差別),而從 (9) 式可以知道,我們目前只關心第一種情況。
註意,為了避免混亂,我們必須宣告一下各個向量的大小。我們假設每個向量都是列向量,經過轉置 ⊤ 之後就代表一個行向量,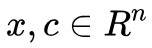 都是 n 維向量,其中 c 也就是權重,
都是 n 維向量,其中 c 也就是權重,![]() 就是對 x 的各個分量加權求和;
就是對 x 的各個分量加權求和;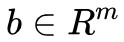 是 m 維向量,自然
是 m 維向量,自然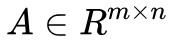 是一個 m×n 的矩陣了, Ax=b 實際上就是描述了 m 個等式約束。
是一個 m×n 的矩陣了, Ax=b 實際上就是描述了 m 個等式約束。
弱對偶形式
在規劃和最佳化問題中,“對偶形式”是一個非常重要的概念。一般情況下,“對偶”是指某種變換,能將原問題轉化為一個等價的、但是看起來幾乎不一樣的新問題,即:

“對偶”之所以稱為“對偶”,是因為將新問題進行同樣形式的變換後,通常來說能還原為原問題,即:

即“對偶”像是一面鏡子,原問題和新問題相當於“原像”和“映象”,解決了一個問題,就等價於解決了另一個問題。所以就看哪個問題更簡單了。
讀者可能還有疑問:“對偶”跟數學中諸如“逆否命題”之類的等價描述有什麼區別?其實也沒有本質區別,簡單來說“對偶”和“逆否命題”都是跟原來的命題完全等價的,但是“對偶”看起來跟原命題很不一樣,而“逆否命題”僅僅是原命題的一個邏輯變換。從線性代數的角度來看,“對偶”相當於向量空間中的“原空間”和“補空間”之間的關係。
最大 vs 最小
這裡我們先介紹“弱對偶形式”,其實它推導起來還是挺簡單的。
我們的標的是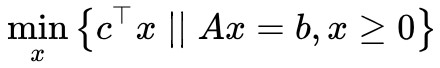 ,設定最小值在
,設定最小值在![]() 處取到,那麼我們有
處取到,那麼我們有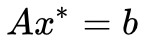 ,我們可以在兩邊乘以一個
,我們可以在兩邊乘以一個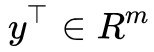 ,使得等式變成一個標量:
,使得等式變成一個標量: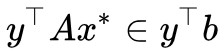 。
。
如果此時假設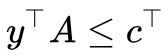 ,那麼
,那麼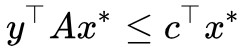 (因為
(因為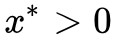 ),則
),則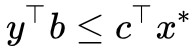 。也就是說,在條件
。也就是說,在條件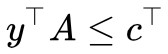 下的任意
下的任意![]() 總是不大於
總是不大於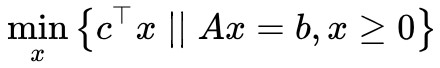 ,“總是”意味著即使對於最大那個也一樣,所以我們就有:
,“總是”意味著即使對於最大那個也一樣,所以我們就有:
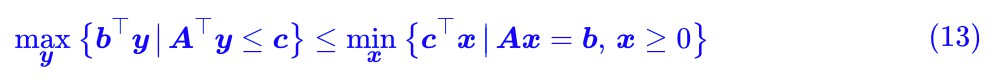
這便稱為“弱對偶形式”,它的形式就是:“左邊的最大”還大不過“右端的最小”。
幾點評註
對於弱對偶形式,也許下麵幾點值得進一步說明一下:
1. 現在我們將原來的最小值問題變成了一個最大值問題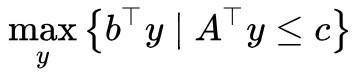 ,這便有了對偶的味道。當然,弱對偶形式之所以“弱”,是因為我們目前找到的對偶形式只是原來問題的一個下界,還沒有證明它們二者相等。
,這便有了對偶的味道。當然,弱對偶形式之所以“弱”,是因為我們目前找到的對偶形式只是原來問題的一個下界,還沒有證明它們二者相等。
2. 弱對偶形式在很多最佳化問題中(包括非線性最佳化)都成立。如果二者真的相等,那麼就是真正意義上的對偶了,稱為強對偶形式。
3. 理論上,我們確實需要證明式 (13) 左右兩端相等才能進一步應用它。但從應用角度,其實弱對偶形式給出的下界都已經夠用了,因為深度學習中的問題都很複雜,能有一個近似的標的去最佳化都已經很不錯了。
4. 讀者可能會想問:前面我們為什麼要假設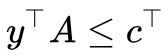 而不乾脆假設
而不乾脆假設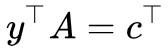 ?假設後者當然簡單很多,但問題是後者在實踐中很難實現,所以只能假設前者。
?假設後者當然簡單很多,但問題是後者在實踐中很難實現,所以只能假設前者。
強對偶形式
上面已經說了,從實踐角度其實弱對偶形式已經夠用了。但是為了讓對完整理論的讀者也有更多收穫,這裡繼續把“強對偶形式”也論證一番。對於只關心 WGAN 本身的讀者來說,可以考慮跳過這部分。
所謂強對偶形式,也就是:
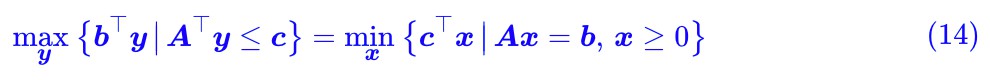
註意前面已經說了,弱對偶形式對於很多最佳化問題都成立,但強對偶形式不一定成立。而對於線性規劃來說,強對偶形式是成立的。
Farkas引理
強對偶形式的證明,主要用到稱之為“Farkas 引理”的結論:
對於固定的矩陣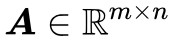 和向量
和向量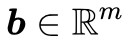 ,下麵兩個選項有且只有一個成立:
,下麵兩個選項有且只有一個成立:
1. 存在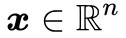 且 x≥0,使得Ax=b;
且 x≥0,使得Ax=b;
2. 存在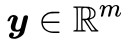 使得
使得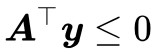 且
且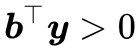 。
。
什麼鬼?又大又小又轉置的?能不能說人話?
其實這個引理還真有一個很直觀的幾何解釋,只不過幾何解釋翻譯成代數語言就不簡單了。幾何解釋的出發點是我們去考慮如下的向量集合:
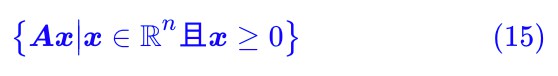
這個集合的含義是:我們將 A 看成是 n 個 m 維列向量的組合。
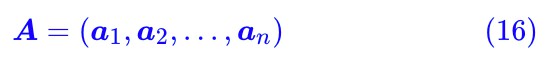
那麼上述集合實際上就是所有 a1,a2,…,an 的非負線性組合。那這個集合是個啥呢?答案是:一個錐,如圖所示。
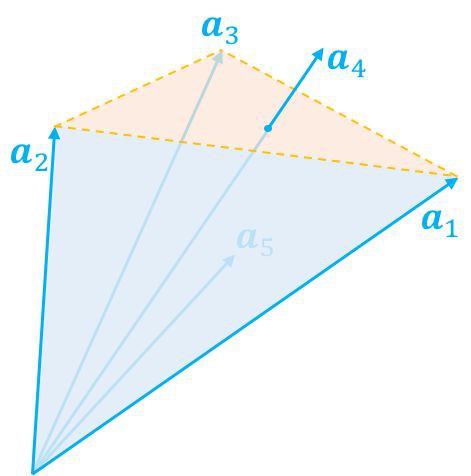
▲ 給定向量的非負線性組合構成這些向量圍成的一個錐
現在我們隨便給定一個向量 b,那麼顯然它只有兩種可能性,而且必有一種成立:1. 在錐內(包括邊界);2. 在錐外。這當然是廢話,但是將它翻譯成代數語言,那就不是廢話了。
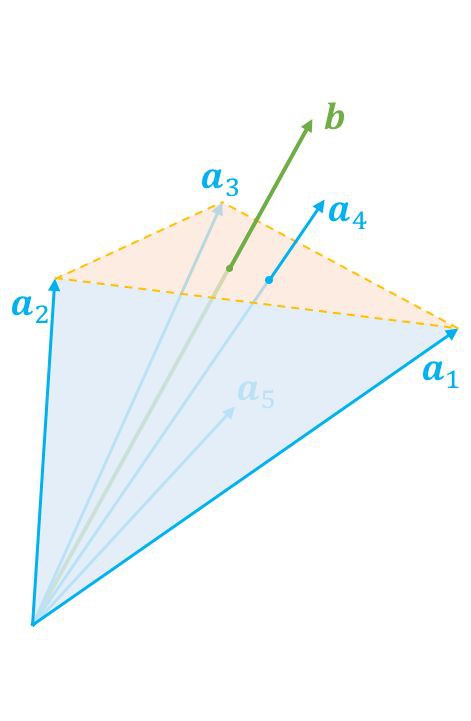
▲ 給定的向量在錐內,意味著可以表示為非負線性組合
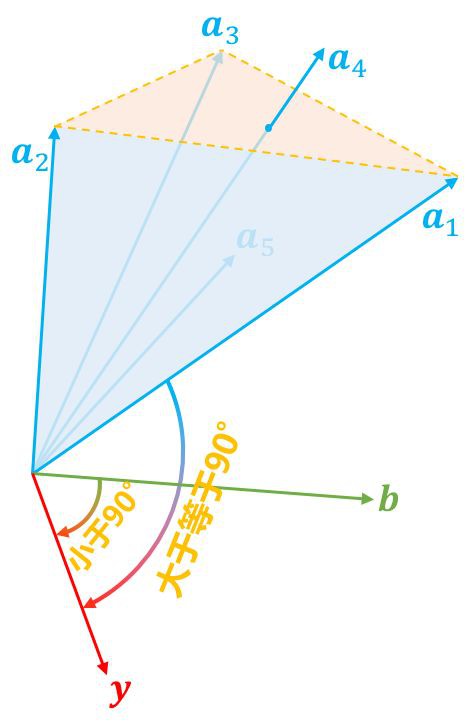
▲ 給定的向量在錐外,我們可以找到一個“標桿”向量與之對比
如果它在錐內,那麼根據錐本身的定義,它就可以表示為 a1,a2,…,an 的非負線性組合(表示方式可能不唯一),也就是存在 x≥0,使得 Ax=b,這就是第一種情況。
如果在錐外呢?怎麼表示在錐外?當然我們可以直接寫出錐內的否命題,但是那實用價值不大。如果向量 b 在錐外,那麼我們總是可以找到一個“標桿”向量 y,它與 a1,a2,…,an 的夾角都大於等於 90 度,向量表示法就是內積都小於等於零,即 ,或者寫成一個整體
,或者寫成一個整體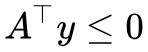 。
。
找到這個“標桿”後,向量 b 與“標桿”的夾角必然是要小於 90 度的,即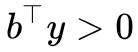 。這樣一個大於等於 90 度,一個小於 90 度,保證了向量 b 在全體向量構成的錐外。這就是第二種情況。
。這樣一個大於等於 90 度,一個小於 90 度,保證了向量 b 在全體向量構成的錐外。這就是第二種情況。
當然,這不能算是完備的證明,只能算是一個啟髮式引導,完備的證明還要仔細論證為什麼這些向量的非負線性組合構成了一個錐。這些就不在本文的範疇了。Farkas 引理的特點是二選一,比如我要證明滿足第二點,只需要證明它不滿足第一點,反之亦然。這是對問題的一個轉化。
從引理到強對偶
有了 Farkas 引理,我們就可以證明強對偶形式了。證明的思路是:證明 max 可以任意程度地接近 min 。
證明還是先假設 min 的最小值在![]() 處取到,即最小值為
處取到,即最小值為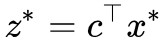 ,那麼我們考慮:
,那麼我們考慮:
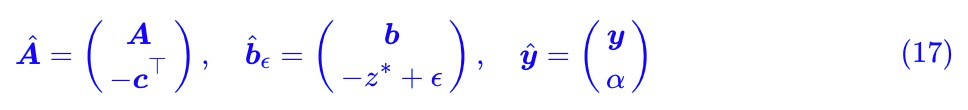
當 ϵ>0 時,那麼對於任意 x≥0,![]() 都不可能等於
都不可能等於![]() ,這是因為
,這是因為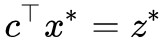 已經是最小值,所以
已經是最小值,所以![]() 是
是![]() 能達到的最大值,它不可能等於更大的
能達到的最大值,它不可能等於更大的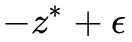 。
。
前面已經說了,不滿足第一種情況,那就只能滿足第二種情況了,即存在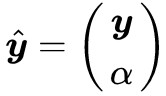 使得
使得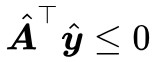 且
且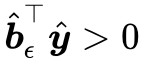 ,這等價於:
,這等價於:
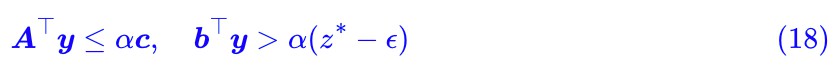
下麵我們表明 α 必須大於 0,這是因為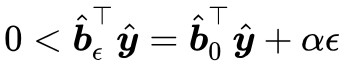 ,所以我們再去考慮 ϵ=0。而當 ϵ=0 時有
,所以我們再去考慮 ϵ=0。而當 ϵ=0 時有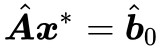 ,即滿足 Farkas 引理的第一種情況,那就不滿足第二種情況,而不滿足第二種情況,意味著
,即滿足 Farkas 引理的第一種情況,那就不滿足第二種情況,而不滿足第二種情況,意味著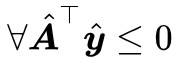 ,都有
,都有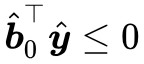 ,剛剛我們已經證明瞭
,剛剛我們已經證明瞭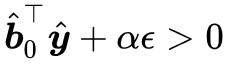 ,所以必須有 α>0。
,所以必須有 α>0。
現在確定 α>0 了,我們就可以從式 (18) 得到:
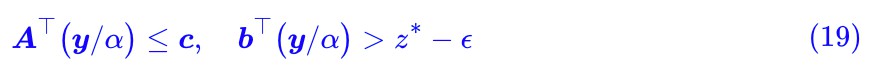
這意味著:
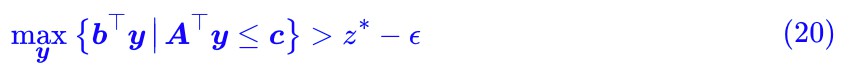
而弱對偶形式已經告訴我們:

也就是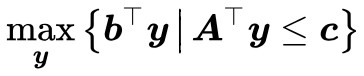 被夾在
被夾在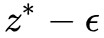 和
和![]() 之間,而因為 ϵ > 0 是任意的,所以兩者可以無限接近,從而:
之間,而因為 ϵ > 0 是任意的,所以兩者可以無限接近,從而:
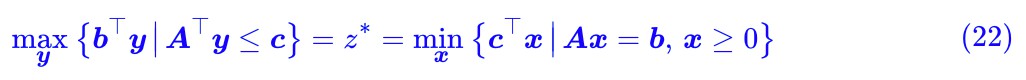
這便是要證的強對偶形式。
簡單說明
Farkas 引理和強對偶形式的證明,看上去比較迂迴,但實際上是最佳化理論中非常經典和重要的證明案例,對於初學者來說,它應該是一次非常強烈的思維衝擊。因為我們以往的認識中,我們對原命題做變換,僅僅是侷限於“邏輯變換”,如否命題、逆否命題等。而對偶形式和 Farkas 引理卻出現了一些“看起來很不一樣,卻又偏偏等價”的結論。
Farkas 引理和強對偶形式也可以進一步推廣到一般的凸集最佳化問題,證明手段相似,只不過在對區域和不等關係的討論上,比上面的線性規劃的過程更為細緻和複雜。不過我也不是專門搞這些最佳化問題的,所以只有一個模糊的認識,就不再繼續班門弄斧了。
Wasserstein GAN
好了,進行了一大通的準備工作後,我們終於可以匯出 Wasserstein GAN 了,就本文來看,它只不過是線性規劃的對偶形式的一個副產品罷了。
W距離的對偶
在推導之前,我們還是再來捋一捋本文的思路:本文先給出了 W 距離的定義 (1) ,然後經過分析,發現它其實就是普通線性規劃問題的一個連續版本,轉化過程為 (7) , (8) 和 (9) ;因此中間我們花了相當一部分篇幅去學習線性規劃及其對偶形式,最終得到了結論 (14) 。
現在我們要做的事情,就是把整個過程“逆”過來,也就是將找出 (14) 對應的連續版本,為 W 距離找一個對偶運算式。 其實這個過程也不複雜,由結論 (14) 和式 (9) ,我們得到:
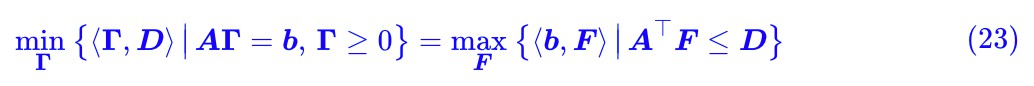
註意式 (8) 中 b 是由兩部分拼起來的,所以我們也可以把 F 類似地寫成:

現在 ⟨b,F⟩ 可以寫成:
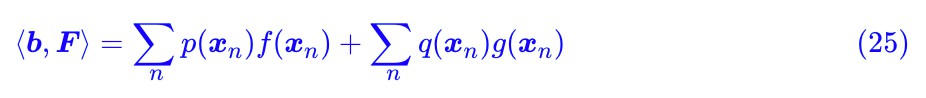
或者對應的積分形式是:
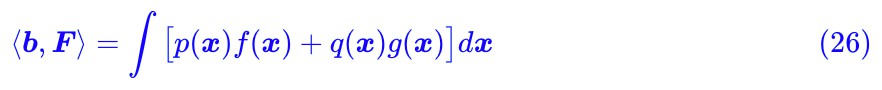
別忘了約束條件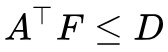 :
:
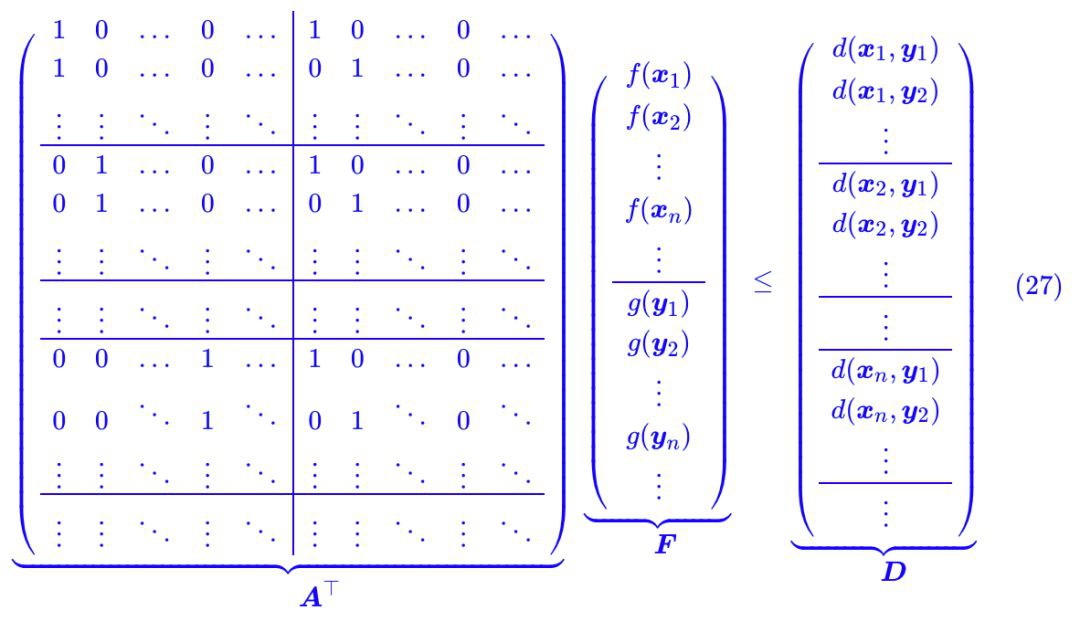
代入計算後,可以發現這個諾大的矩陣運算實際上就說了這樣的一件事情:
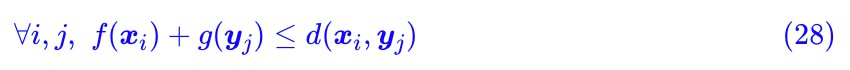
或者直接寫成:

從對偶到WGAN
終於,我們就要接近尾聲了,現在我們得到了 W 距離 (1) 的一個對偶形式了:
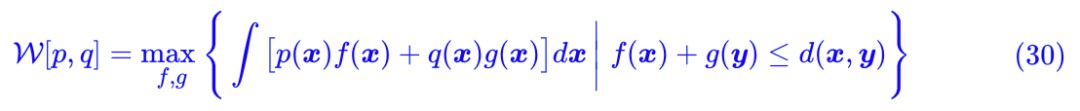
註意到由 f(x)+g(y)≤d(x,y) 我們得到:

即 g(x)≤−f(x),所以我們有:
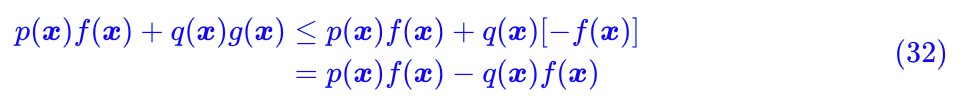
即如果 g=−f,它的最大值不會小於原來的最大值,所以我們可以放心地讓 g=−f,從而:
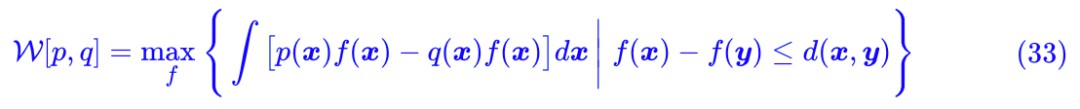
這便是我們最終要尋找的 W 距離 (1) 的對偶形式了,其中約束條件我們可以寫為 ||f||L≤1,稱為 Lipschitz 約束。
由於 p,q 都是機率分佈,因此我們可以寫成取樣形式:
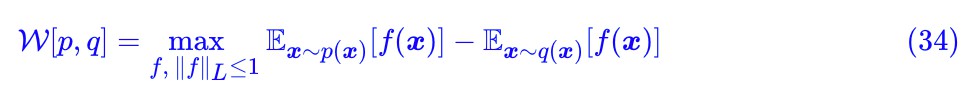
這就是 WGAN 的判別器所採用的 loss 了,自然地,整個 WGAN 的訓練過程就是:
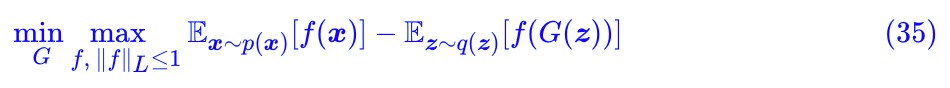
千呼萬喚的 WGAN 終於現身,剩下的就是怎麼加 Lipschitz 約束的問題了,可以參考:深度學習中的Lipschitz約束:泛化與生成模型。
文章小結
本文主要介紹了 Wasserstein 距離,然後轉化為一個線性規劃問題,繼而介紹了線性規劃的對偶理論,最終匯出了 Wasserstein 距離的對偶形式,它可以用作訓練生成模型,即 WGAN 及後面一系列推廣。
本文是筆者對線性規劃及其對偶理論的一次簡單學習總結,對熟悉線性代數後希望從理論上瞭解 WGAN 的讀者應該會有一定的參考價值。如果對文中內容有什麼疑惑或批評,歡迎留言指出。
 知識星球
知識星球