循序漸進帶你學習時間複雜度和空間複雜度

（給演演算法愛好者加星標，修煉程式設計內功）

作者：Rocky0429 （本文來自作者投稿，簡介見末尾）

前言

我們都知道，對於同一個問題來說，可以有多種解決問題的演演算法。儘管演演算法不是唯一的，但是對於問題本身來說相對好的演演算法還是存在的，這裡可能有人會問區分好壞的標準是什麼？這個要從「時效」和「儲存」兩方面來看。

人總是貪婪的，在做一件事的時候，我們總是期望著可以付出最少的時間、精力或者金錢來獲得最大的回報，這個類比到演演算法上也同樣適用，那就是花最少的時間和最少的儲存做成最棒的解決辦法，所以好的演演算法應該具備時效高和儲存低的特點。這裡的「時效」是指時間效率，也就是演演算法的執行時間，對於同一個問題的多種不同解決演演算法，執行時間越短的演演算法效率越高，越長的效率越低；「儲存」是指演演算法在執行的時候需要的儲存空間，主要是指演演算法程式執行的時候所佔用的記憶體空間。

時間複雜度

首先我們先來說時間效率的這個問題，這裡的時間效率就是指的演演算法的執行時間，時間的快慢本來就是一個相對的概念，那麼到了演演算法上，我們該用怎樣的度量指標去度量一個演演算法的時間效率（執行時間）呢？

剛開始我們想出了一種事後統計方法，我稱它為「馬後炮式」，顧名思義，就是對於要解決的某個問題，費盡心思想了 n 種解法，提前寫好演演算法程式，然後攢了一堆資料，讓它們分別在電腦上跑，跑完瞭然後比較程式的執行時間，根據這個來判斷演演算法時效的高低。這種的判斷技術計算的是我們日常所用的時間，但這並不是一個對我們來說有用的度量指標，因為它還依賴於執行的機器、所用的程式語言、編譯器等等等等。相反，我們需要的是一個不依賴於所用機器或者程式語言的度量指標，這種度量指標可以幫助我們判斷演演算法的優劣，並且可以用來比較演演算法的具體實現。

我們的科學家前輩們發現當我們試圖去用執行時間作為獨立於具體程式或計算機的度量指標去描述一個演演算法的時候，確定這個演演算法所需要的步驟數目非常重要。如果我們把演演算法程式中的每一步看作是一個基本的計量單位，那麼一個演演算法的執行時間就可以看作是解決一個問題所需要的總步驟數。但是由於演演算法的執行過程又各不相同，所以這個每一步，即這個基本的計量單位怎麼去選擇又是一個令人頭禿的問題。

下麵我們來看一個簡單的求和的函式：

def get_sum(n):
          sum = 0
   for i in range(1,n+1):
         sum += i
   return sum
print(get_sum(10))

我們仔細去分析一下上述程式碼，其實可以發現統計執行求和的賦值陳述句的次數可能是一個好的基本計數單位，在上面 get_sum 函式中，賦值陳述句的數量是 1 （sum = 0）加上 n （執行 sum += i 的次數）。

我們一般用一個叫 T 的函式來表示賦值陳述句的總數量，比如上面的例子可以表示成 T(n) = n + 1。這裡的 n 一般指的是「資料的規模大小」，所以前面的等式可以理解為「解決一個規模大小為 n，對應 n+1 步操作步數的問題，所需的時間為 T(n)」。

對於 n 來說，它可以取 10，100，1000 或者其它更大的數，我們都知道求解大規模的問題所需的時間比求解小規模要多一些，那麼我們接下來的標的就很明確了，那就是「尋找程式的執行時間是如何隨著問題規模的變化而變化」。

我們的科學家前輩們又對這種分析方法進行了更為深遠的思考，他們發現有限的操作次數對於 T(n) 的影響，並不如某些佔據主要地位的操作部分重要，換句話說就是「當資料的規模越來越大時，T(n) 函式中的某一部分掩蓋了其它部分對函式的影響」。最終，這個起主導作用的部分用來對函式進行比較，所以接下來就是我們所熟知的大 O 閃亮登場的時間了。

大 O 表示法

「數量級」函式用來描述當規模 n 增加時，T(n) 函式中增長最快的部分，這個數量級函式我們一般用「大 O」表示，記做 O(f(n))。它提供了計算過程中實際步數的近似值，函式 f(n) 是原始函式 T(n) 中主導部分的簡化表示。

在上面的求和函式的那個例子中，T(n) = n + 1，當 n 增大時，常數 1 對於最後的結果來說越來不越沒存在感，如果我們需要 T(n) 的近似值的話，我們要做的就是把 1 給忽略掉，直接認為 T(n) 的執行時間就是 O(n)。這裡你一定要搞明白，這裡不是說 1 對 T(n) 不重要，而是當 n 增到很大時，丟掉 1 所得到的近似值同樣很精確。

再舉個例子，比如有一個演演算法的 T(n) = 2n^2+ 2n + 1000，當 n 為 10 或者 20 的時候，常數 1000 看起來對 T(n) 起著決定性的作用。但是當 n 為 1000 或者 10000 或者更大呢？n^2 起到了主要的作用。實際上，當 n 非常大時，後面兩項對於最終的結果來說已經是無足輕重了。與上面求和函式的例子很相似，當 n 越來越大的時候，我們就可以忽略其它項，只關註用 2n^2 來代表 T(n) 的近似值。同樣的是，繫數 2 的作用也會隨著 n 的增大，作用變得越來越小，從而也可以忽略。我們這時候就會說 T(n) 的數量級 f(n) = n^2，即 O(n^2)。

最好情況、最壞情況和平均情況

儘管前面的兩個例子中沒有體現，但是我們還是應該註意到有時候演演算法的執行時間還取決於「具體資料」而不僅僅是「問題的規模大小」。對於這樣的演演算法，我們把它們的執行情況分為「最優情況」、「最壞情況」和「平均情況」。

某個特定的資料集能讓演演算法的執行情況極好，這就是最「最好情況」，而另一個不同的資料會讓演演算法的執行情況變得極差，這就是「最壞情況」。不過在大多數情況下，演演算法的執行情況都介於這兩種極端情況之間，也就是「平均情況」。因此一定要理解好不同情況之間的差別，不要被極端情況給帶了節奏。

對於「最優情況」，沒有什麼大的價值，因為它沒有提供什麼有用資訊，反應的只是最樂觀最理想的情況，沒有參考價值。「平均情況」是對演演算法的一個全面評價，因為它完整全面的反映了這個演演算法的性質，但從另一方面來說，這種衡量並沒有什麼保證，並不是每個運算都能在這種情況內完成。而對於「最壞情況」，它提供了一種保證，這個保證執行時間將不會再壞了，**所以一般我們所算的時間複雜度是最壞情況下的時間複雜度**，這和我們平時做事要考慮到最壞的情況是一個道理。

在我們之後的演演算法學習過程中，會遇到各種各樣的數量級函式，下麵我給大家列舉幾種常見的數量級函式：

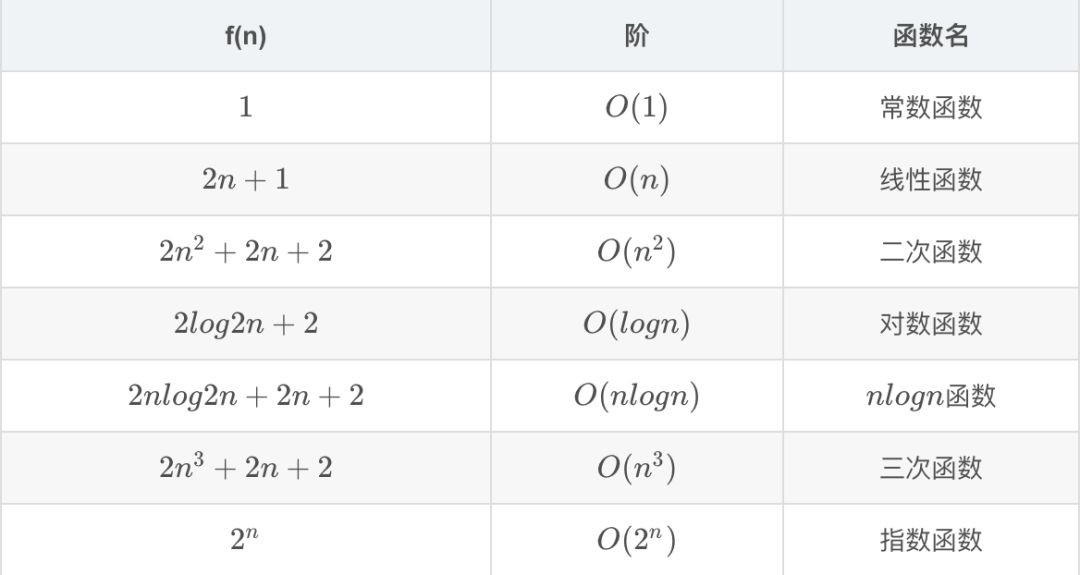
為了確定這些函式哪些在 T(n) 中佔主導地位，就要在 n 增大時對它們進行比較，請看下圖（圖片來自於 Google 圖片）：

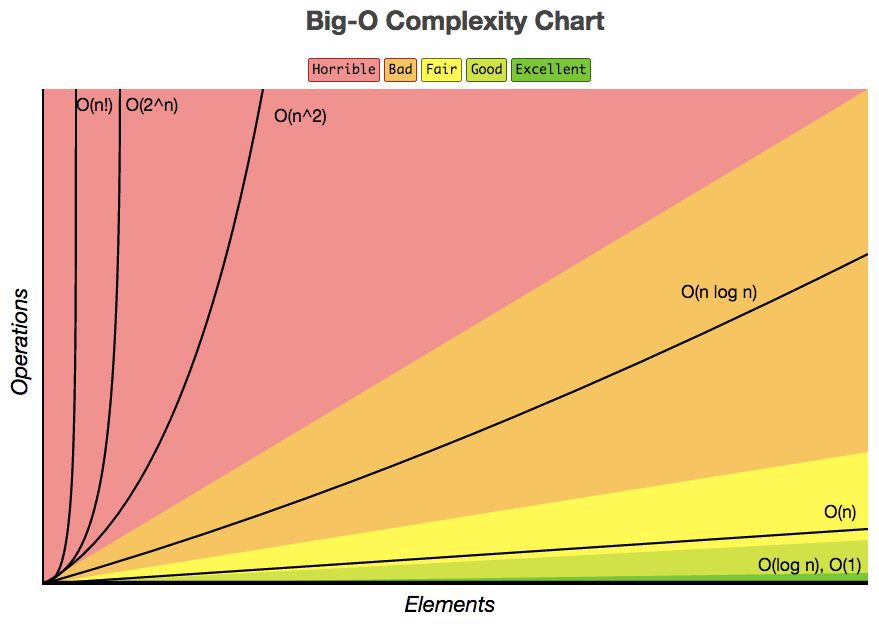
在上圖中，我們可以看到當 n 很小時，函式之間不易區分，很難說誰處於主導地位，但是當 n 增大時，我們就能看到很明顯的區別，誰是老大一目瞭然：

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)

我們下麵就來分析幾個上述所說的「數量級函式」：

1.常數函式

n = 100  # 1 次
sum  = (1 + n) *n / 2 # 1 次
print(sum) # 1 次

上述演演算法程式的 f(n) = 3，可能有人看到這會說那麼時間複雜度就是 O(f(n)) = O(3)，其實這個是錯的，這個函式的時間複雜度其實是 O(1)。這個對於初學者來說是很難理解的一種結果，其實你可以把 sum = (1 + n) * n / 2 多複製幾次再來看：

a = 100 # 1 次
sum  = (1 + n) * n / 2 # 1 次
sum  = (1 + n) * n / 2 # 1 次
sum  = (1 + n) * n / 2 # 1 次
sum  = (1 + n) * n / 2 # 1 次
sum  = (1 + n) * n / 2 # 1 次
sum  = (1 + n) * n / 2 # 1 次
print(sum) # 1 次

上述演演算法的 f(n) = 8，事實上你可以發現無論 n 為多少，上述兩段程式碼就是 執行 3 次和執行 8 次的區別。這種與資料的規模大小 n 無關，執行時間恆定的演演算法我們就叫它具有 O(1) 的時間複雜度。不管這個常數是多少，我們都記作是 O(1)，而不是 O(3) 或者是 O(8)。

2.對數函式

cnt = 1
while cnt < n:
   cnt *= 2 # O(1)

上面的演演算法程式的時間複雜度就是 O(logn)，這個是怎麼算出來的呢？其實很簡單：上述的程式碼可以解釋成 cnt 乘以多少個 2 以後才能大於等於 n，我們假設個數是 x，也就是求 2^x = n，即 x = log2n，所以這個迴圈的時間複雜度就是 O(logn)。

最後呢，我們來看看下麵的這個例子，藉助這段程式碼來詳細的說一下我們如何對其時間複雜度進行詳細的分析：

a = 1
b = 2
c = 3

for i in range(n):
   for j in range(n):
       x = i * i
       y = j * j
       z = i * j

for k in range(n):
   u = a * k + b
   v = c * c

d = 4

上面的程式碼沒有任何意義，甚至不是一個可執行的程式碼，我只是用來說明你在以後如何對程式碼進行執行分析，關於程式碼本身可不可以執行，就不需要你在這關心了。

上面的程式碼其實我們要分的話可以分成 4 部分：第 1 部分是 a，b，c 這 3 個賦值陳述句，執行次數也就是 3 次；第二部分是 3n^2，因為是迴圈結構，裡面有 x，y，z 這 3 個賦值陳述句，每個陳述句執行了 n^2 次；第 3 部分是 2n，因為裡面是 2 個賦值陳述句，每條陳述句被執行了 n 次；最後第 4 部分是常數 1，只有 d 這麼 1 條賦值陳述句。所以我們得到的 T(n

) = 3+3n^2 +2n+1 = 3n^2+2n+4，看到指數項，我們自然的發現是 n^2 做主導，當 n 增大時，後面兩項可以忽略掉，所以這個程式碼片段的數量級就是 O(n^2)。

空間複雜度

類比於時間複雜度的討論，一個演演算法的空間複雜度是指該演演算法所耗費的儲存空間，計算公式計作：S(n) = O(f(n))。其中 n 也為資料的規模，f(n) 在這裡指的是 n 所佔儲存空間的函式。

一般情況下，我們的程式在機器上執行時，刨去需要儲存程式本身的輸入資料等之外，還需要儲存對資料操作的「儲存單元」。如果輸入資料所佔空間和演演算法無關，只取決於問題本身，那麼只需要分析演演算法在實現過程中所佔的「輔助單元」即可。如果所需的輔助單元是個常數，那麼空間複雜度就是 O(1)。

空間複雜度其實在這裡更多的是說一下這個概念，因為當今硬體的儲存量級比較大，一般不會為了稍微減少一點兒空間複雜度而大動干戈，更多的是去想怎麼最佳化演演算法的時間複雜度。所以我們在日常寫程式碼的時候就衍生出了用「空間換時間」的做法，並且成為常態。比如我們在求解斐波那契數列數列的時候我們可以直接用公式去遞迴求，用哪個求哪個，同樣也可以先把很多結果都算出來儲存起來，然後用到哪個直接呼叫，這就是典型的用空間換時間的做法，但是你說這兩種具體哪個好，偉大的馬克思告訴我們「具體問題具體分析」。

後話

如果上面的文章你仔細看了的話，你會發現我不是直接上來就告訴你怎麼去求時間複雜度，而是從問題的產生，到思考解決的辦法，到“馬後炮”，再到 T(n)，最後到 O(n)一步一步來的。這樣做的原因呢有兩個：一是為了讓你瞭解大 O 到底是怎麼來的，有時候搞明白了由來，對於你接下來的學習和理解有很大的幫助；二是為了讓這個文章看起來不是那麼枯燥，我覺得很多時候上來扔給你一堆概念術語，很容易就讓人在剛看到它的時候就打起了退堂鼓，循序漸進的來，慢慢引導著更容易接受一些。

很多人從大學到工作，程式碼寫了不少依然不會估算時間複雜度，我感覺倒不是學不會，而是內心沒有重視起來。你可能覺得計算機的更新換代很快，CPU 處理速度的能力越來越棒，沒必要在一些小的方面斤斤計較，其實我覺得你是 too young too naive。我們隨便來算一個簡單的例子：有兩臺電腦，你的電腦的運算速度是我的電腦的 100 倍，同樣一道問題，明明稍微想一想用 O(n) 可以做出來，你偏偏要懶，直接暴力 O(n^2)，那麼當 n 的資料稍微增大一些，比如上萬上十萬，到底誰的運算速度快還用我再告訴你嗎？

所以今後在寫演演算法的時候，請好好學會用時間複雜度估算一下自己的程式碼，然後想想有沒有更有效率的方法去改進它，你只要這樣做了，相信慢慢的你的程式碼會寫的越來越好，頭會越來越禿。（逃

最後說一點的是，估算演演算法的複雜度這件事你不要指望一下子看了一篇文章就想弄懂，這個還是要有意識的多練，比如看到一個程式的時候有意識的估算一下它的複雜度，準備動手寫程式碼的時候也想想有沒有更好的最佳化方法，有意識的練習慢慢就會來了感覺。這篇文章我就用了幾個小例子，大概的估算方式就是這樣。

覺得本文有幫助？請分享給更多人

關註「演演算法愛好者」加星標，修煉程式設計內功

微信掃一掃
使用小程式