(給演演算法愛好者加星標,修煉程式設計內功)
作者:帥地 (本文來自作者投稿,簡介見末尾)
二叉堆是一種應用很廣的資料結構,今天,我們就來簡單講講二叉堆。
二叉堆是一種特殊的堆。具有如下的特性:
-
具有完全二叉樹的特性。
-
堆中的任何一個父節點的值都大於等於它左右孩子節點的值,或者都小於等於它左右孩子節點的值。
根據第二條特性,我們又可以把二叉堆分成兩類:
1、最大堆:父節點的值大於等於左右孩子節點的值。

2、最小堆:父節點的值小於等於左右孩子節點的值。

我們把二叉堆的根節點稱之為堆頂。根據二叉堆的特性,堆頂要嘛是整個堆中的最大元素,要嘛是最小元素。
今天,我們主要來講講二叉堆的三個主要操作:
-
插入一個節點。
-
刪除一個節點。
-
構建一個二叉堆。
不過這裡需要註意的是,在二叉堆這種結構中,對於刪除一個節點,我們一般刪的是根節點。
下麵我們以最小堆為例子,來講講這些操作。
剛才我們說二叉堆具有完全二叉樹的特性,因此,我們在插入一個節點的時候,應該先保證節點插入後,它仍然是一顆完全二叉樹,然後再來進行調整,使它滿足二叉堆的另一個特性。
所以,在插入的時候,我們把新節點插到完全二叉樹的最後一個位置。例如:

插入0。

之後我們再來進行調整,調整的原則是:讓新插入的節點與它的父節點進行比較,如果新節點小於父節點,則讓新節點上浮,即和父節點交換位置。
上浮之後繼續和它的父節點進行比較,直到父節點的值小於或等於該節點,才停止上浮,即插入結束。例如:
0比5小,上浮。

0比2小於,上浮。

0比1小,上浮。
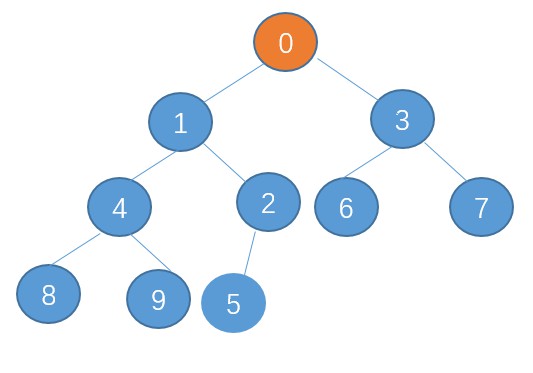
已經到達堆頂了,插入結束。
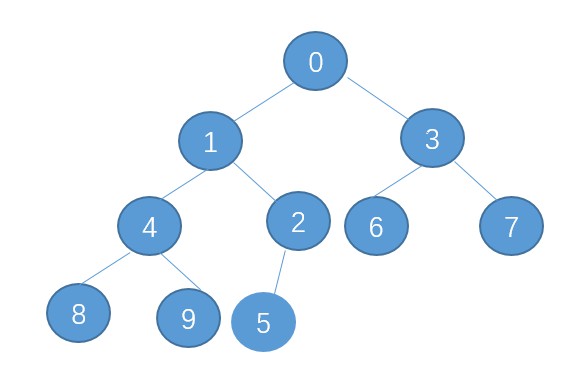
前面說了,刪除節點一般刪除的是根節點。
和插入一樣,由於二叉堆具有完全二叉樹的特性,因為刪除時候,首先我們是要馬上恢復它具有完全二叉樹的特性,所以我們是採取這樣的策略:把根節點刪除之後,用二叉堆的最後一個元素頂替上來,然後在進行調整恢復。例如:

把0刪除了之後,5替換上來。
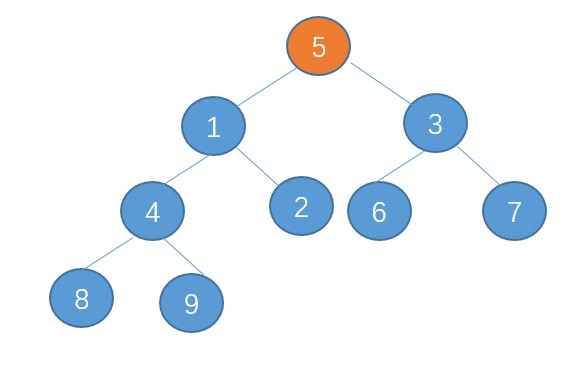
之後再來調整,調整的規則和插入差不多類似,採取下沉的策略:讓5和左右孩子節點相比較,如果左右節點有小於5的,則讓那個較小的孩子代替5的位置,然後5下沉。
下沉之後,5繼續和左右孩子相比,直到左右孩子都大於或等於5才結束。
如:5比1,3都大,1代替5的位置

5比4,2都大,2代替5的位置。

5已經不在具有左右孩子了,刪除結束。

所謂構建,就是給你一個有n個節點的無序的完全二叉樹,然後把它構建成二叉堆。
剛才我們在刪除一個節點的時候,把最後一個元素補到根元素的位置上去,然後再讓這個元素依次下沉,實際上,在這個元素還沒有下沉之前,它就可以看作是一顆無序的完全二叉樹了。
也就是說,要把一個無序的完全二叉樹調整為二叉堆,我們可以讓所有非葉子節點依次下沉。不過下沉的順序不是從根節點開始下沉(想一下相必你就 知道不能從根節點開始下沉),而是從下麵的非葉子節點下稱,在依次往上。舉個例子:
對於這樣一顆無序的完全二叉樹

8進行下沉。
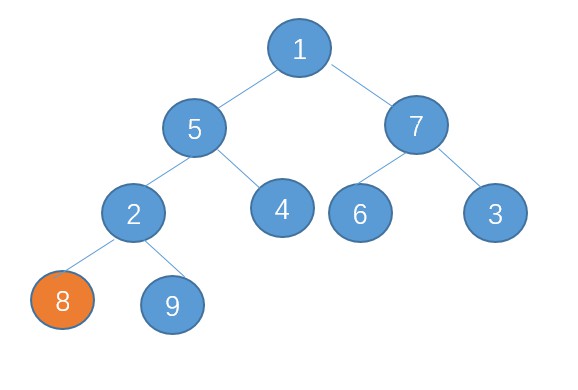
接著,5進行下沉。

2沒問題,之後讓7進行下沉
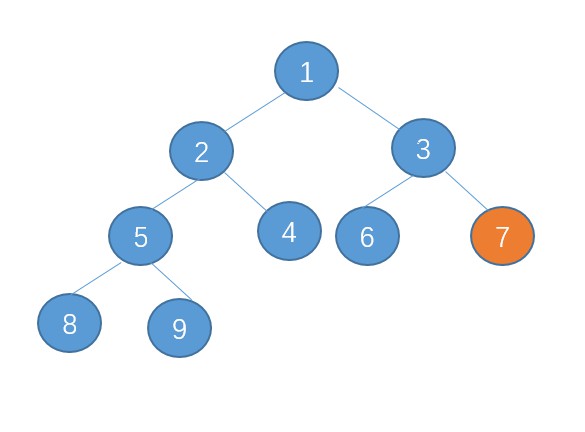
調整完成,構建結束。

不過這裡需要說明的是,我們二叉樹一般是採用連結串列的方式來實現的,但二叉堆我們是採用陣列的方式來儲存的。

如果知道了一個節點的位置,如何知道一個節點的左右孩子節點的位置呢?
這其實不難,根據完全二叉樹的特點,假如一個節點的下標為n,則可以求得它左孩子的下標為:2 n+1;右孩子下標為:2 n+2。
下麵是構建程式碼的實現:
public class BinaryHeap {
/**上浮操作,對插入的節點進行上浮
*
* @param arr
* @param length :表示二叉堆的長度
*/
public static int[] upAdjust(int arr[], int length){
//標記插入的節點
int child = length - 1;
//其父親節點
int parent = (child - 1)/2;
//把插入的節點臨時儲存起來
int temp = arr[child];
//進行上浮
while (child > 0 && temp < arr[parent]) {
//其實不用進行每次都進行交換,單向賦值就可以了
//當temp找到正確的位置之後,我們再把temp的值賦給這個節點
arr[child] = arr[parent];
child = parent;
parent = (child - 1) / 2;
}
//退出迴圈代表找到正確的位置
arr[child] = temp;
return arr;
}
/**
*/
/**
* 下沉操作,執行刪除操作相當於把最後
* * 一個元素賦給根元素之後,然後對根元素執行下沉操作
* @param arr
* @param parent 要下沉元素的下標
* @param length 陣列長度
*/
public static int[] downAdjust(int[] arr, int parent, int length) {
//臨時保證要下沉的元素
int temp = arr[parent];
//定位左孩子節點位置
int child = 2 * parent + 1;
//開始下沉
while (child < length) {
//如果右孩子節點比左孩子小,則定位到右孩子
if (child + 1 < length && arr[child] > arr[child + 1]) {
child++;
}
//如果父節點比孩子節點小或等於,則下沉結束
if (temp <= arr[child])
break;
//單向賦值
arr[parent] = arr[child];
parent = child;
child = 2 * parent + 1;
}
arr[parent] = temp;
return arr;
}
/**
* 構建操作
*
* @param arr
*/
public static int[] buildHead(int[] arr,int length) {
//從最後一個非葉子節點開始下沉
for (int i = (length - 2) / 2; i >= 0; i--) {
arr = downAdjust(arr, i, length);
}
return arr;
}
}
本次講解到此結束。下篇繼續講解和堆有關的知識點。至於bitmap演演算法最佳化的那篇,會在之後給出。
【本文作者】
帥地:一個熱愛程式設計的在校生,我的世界不只有coding,還有writing。目前維護訂閱號「苦逼的碼農」,專註於寫計算機網路,資料結構等相關文章。
推薦閱讀 (點選標題可跳轉閱讀)
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」加星標,修煉程式設計內功
 知識星球
知識星球