漫畫：什麼是計數排序？

這段程式碼在一開頭補充了一個步驟，就是求得數列的最大整數值max。後面建立的統計陣列countArray，長度就是max+1，以此保證陣列的最後一個下標是max。

95，94，91，98，99，90，99，93，91，92

怎麼解決這個問題呢？

很簡單，我們不再以（輸入數列的最大值+1）作為統計陣列的長度，而是以（數列最大值和最小值的差+1）作為統計陣列的長度。

同時，數列的最小值作為一個偏移量，用於統計陣列的對號入座。

以剛才的數列為例，統計陣列的長度為  99-90+1 = 10 ，偏移量等於數列的最小值 90 。

對於第一個整數95，對應的統計陣列下標是 95-90 = 5，如圖所示：

什麼意思呢？讓我們看看下麵的例子：

給定一個學生的成績表，要求按成績從低到高排序，如果成績相同，則遵循原表固有順序。

那麼，當我們填充統計陣列以後，我們只知道有兩個成績併列95分的小夥伴，卻不知道哪一個是小紅，哪一個是小綠：

下麵的講解會有一些燒腦，請大家扶穩坐好。我們仍然以剛才的學生成績表為例，把之前的統計陣列變形成下麵的樣子：

這是如何變形的呢？統計陣列從第二個元素開始，每一個元素都加上前面所有元素之和。

為什麼要相加呢？初次看到的小夥伴可能會覺得莫名其妙。

這樣相加的目的，是讓統計陣列儲存的元素值，等於相應整數的最終排序位置。比如下標是9的元素值為5，代表原始數列的整數9，最終的排序是在第5位。

接下來，我們建立輸出陣列sortedArray，長度和輸入數列一致。然後從後向前遍歷輸入數列：

第一步，我們遍歷成績表最後一行的小綠：

小綠是95分，我們找到countArray下標是5的元素，值是4，代表小綠的成績排名位置在第4位。

同時，我們給countArray下標是5的元素值減1，從4變成3,，代表著下次再遇到95分的成績時，最終排名是第3。

第二步，我們遍歷成績表倒數第二行的小白：

小白是94分，我們找到countArray下標是4的元素，值是2，代表小白的成績排名位置在第2位。

同時，我們給countArray下標是4的元素值減1，從2變成1,，代表著下次再遇到94分的成績時（實際上已經遇不到了），最終排名是第1。

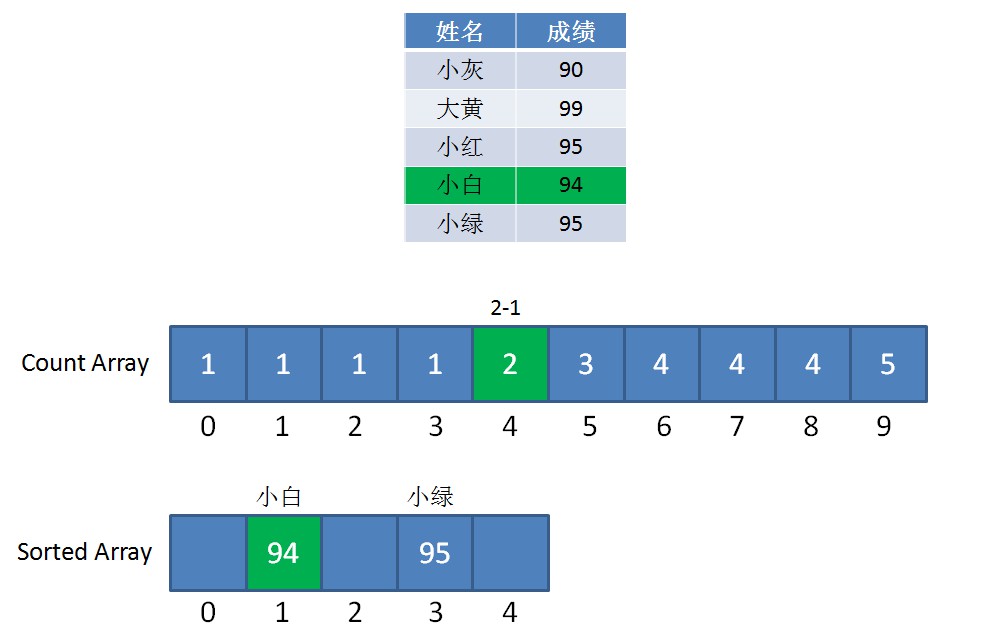
第三步，我們遍歷成績表倒數第三行的小紅：

小紅是95分，我們找到countArray下標是5的元素，值是3（最初是4，減1變成了3），代表小紅的成績排名位置在第3位。

同時，我們給countArray下標是5的元素值減1，從3變成2,，代表著下次再遇到95分的成績時（實際上已經遇不到了），最終排名是第2。

這樣一來，同樣是95分的小紅和小綠就能夠清楚地排出順序了，也正因此，最佳化版本的計數排序屬於穩定排序。

後面的遍歷過程以此類推，這裡就不再詳細描述了。

public static int[] countSort(int[] array) {
    //1.得到數列的最大值和最小值，並算出差值d
    int max = array[0];
    int min = array[0];
    for(int i=1; i
        if(array[i] > max) {
            max = array[i];
        }
        if(array[i] < min) {
            min = array[i];
        }
    }
    int d = max - min;
    //2.建立統計陣列並統計對應元素個數
    int[] countArray = new int[d+1];
    for(int i=0; i
        countArray[array[i]-min]++;
    }
    //3.統計陣列做變形，後面的元素等於前面的元素之和
    int sum = 0;
    for(int i=0;i
        sum += countArray[i];
        countArray[i] = sum;
    }
    //4.倒序遍歷原始數列，從統計陣列找到正確位置，輸出到結果陣列
    int[] sortedArray = new int[array.length];
    for(int i=array.length-1;i>=0;i--) {
        sortedArray[countArray[array[i]-min]-1]=array[i];
        countArray[array[i]-min]--;
    }
    return sortedArray;
}
public static void main(String[] args) {
    int[] array = new int[] {95,94,91,98,99,90,99,93,91,92};
    int[] sortedArray = countSort(array);
    System.out.println(Arrays.toString(sortedArray));
}