怎樣用Python實現統計、機率、機器學習基礎實驗？一文看懂

作者：Christian Pascual

參與：王淑婷、思源

來源：機器之心（ID：almosthuman2014）編譯

要學習統計，就不可避免得先瞭解機率問題。機率涉及諸多公式和理論，容易讓人迷失其中，但它在工作和日常生活中都具有重要作用。先前我們已經討論過描述性統計中的一些基本概念，現在，我們將探討統計和機率的關係。

前提條件：

本文不要求讀者具備統計知識，但至少要對 Python 有一個基本的瞭解。考慮到讀者可能不太瞭解 for 迴圈和串列, 下麵將先對它們做個簡單的介紹。

01 什麼是機率？

從最基本的層面上來說，機率要回答的是一個這樣的問題：「一個事件發生的機率是多少？」為了計算某個事件發生的機率，我們還要考慮其它所有可能發生的事件。

機率問題的典型代表是扔硬幣。在扔硬幣的過程中，只會產生兩種結果：

 1. 正面朝上

 2. 反面朝上

這兩種結果構成了一個樣本空間，即所有可能結果的集合。為了計算一個事件發生的機率，我們要統計該事件發生（比如將硬幣擲為正面朝上）的次數，並用它除以總試驗次數。因此，機率會告訴我們，把一枚硬幣擲為正面朝上或反面朝上的機率為 1/2。透過觀察可能發生的事件，機率可以為我們提供一個預測事件發生頻率的框架。

然而，即使結果看起來很明顯，但如果我們真的試著去扔一些硬幣，我們很可能得到過高或過低的正面朝上機率。假設扔硬幣的做法不公平，那我們能做什麼？收集資料！我們可以使用統計法來計算基於真實世界觀察樣本的機率，並將其與理想中的機率做對比。

02 從統計到機率

透過扔 10 次硬幣並計算正面朝上的次數，我們可以獲得資料。我們把這 10 次扔硬幣的過程當做試驗，而硬幣正面朝上的次數將是資料點。也許正面朝上的次數不是「理想的」5 次，但不必著急，因為一次試驗只是一個資料點。

如果進行多次試驗，那我們預計所有試驗正面朝上的的平均機率將接近 50%。下麵的程式碼分別模擬了 10 次、100 次、1000 次和 1000000 次試驗，然後計算了正面朝上的平均頻率。下圖是對這一過程的總結。

import random
def coin_trial():
    heads = 0
    for i in range(100):
        if random.random() <= 0.5:
            heads +=1
    return heads

def simulate(n):
   trials = []
   for i in range(n):
       trials.append(coin_trial())
   return(sum(trials)/n)

simulate(10)
>> 5.4

simulate(100)
>>> 4.83

simulate(1000)
>>> 5.055

simulate(1000000)
>>> 4.999781

coin_trial 函式代表了 10 次硬幣投擲的模擬。它使用 random() 函式來生成一個介於 0 和 1 之間的隨機浮點數，如果浮點數在 0.5 以下，它會增加 heads（正面朝上）次數。然後，simulate 根據你想要的次數來重覆這些試驗，並傳回所有試驗後正面朝上的平均次數。

硬幣投擲模擬的結果很有趣。首先，模擬的資料顯示正面朝上的平均次數接近機率估計的結果。其次，隨著試驗次數的增加，這個 平均數也更加接近預期結果。做 10 次模擬時，有輕微的誤差，但試驗次數為 1000000 次時，誤差幾乎完全消失。隨著我們增加試驗次數，與預期平均數的偏差在不斷減小。聽起來很耳熟是不是？

當然，我們可以自己扔硬幣，但是透過在 Python 程式碼中模擬這一過程可以為節省大量時間。隨著我們獲得越來越多的資料，現實世界（結果）開始與理想世界（預期）重合。因此，給定足夠的資料，統計就可以讓我們根據現實世界的觀察來估計機率。機率提供了理論，而統計提供了使用資料來檢驗該理論的工具。於是，統計樣本的數值特徵，特別是均值和標準差，成為了理論的替代。

你可能會問：「如果我本來就可以計算理論機率，那我為什麼還要用一個替代品？」投擲硬幣是一個非常簡單的例子，但有些更有趣的機率問題並沒有這麼容易計算。隨著時間的推移，一個人患病的可能性有多大？當你開車時，一個關鍵的汽車部件出故障的機率是多少？

計算機率沒有什麼簡單的方法，所以我們必須依靠資料和統計。給定更多的資料，我們的結果有更多的置信度，確信計算結果代表了這些重要事件發生的真實機率。

假設我是一名在職侍酒師，購買之前，我要先弄清楚哪些葡萄酒品質更優。我手頭已有很多資料，所以我們將使用統計資料來指導決策。

03 資料和分佈

在解決「哪種葡萄酒更好」的問題之前，我們需要註意資料的性質。直觀來說，我們想透過打分來選出比較好的葡萄酒，但問題是：分數通常分佈在一個範圍內。那我們要如何比較不同型別葡萄酒的得分，併在一定程度上確定一種葡萄酒比另一種更好呢？

若有一個正態分佈（也稱為高斯分佈），它是機率和統計領域中一個特別重要的現象。正態分佈如下所示：

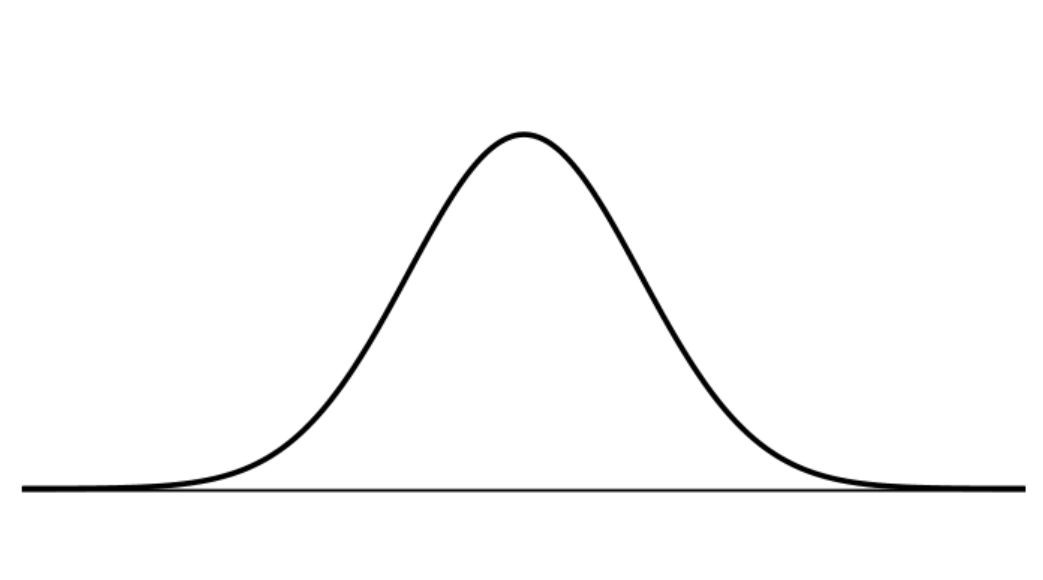
正態分佈最重要的特質是對稱性和形狀，以及其廣泛的普適性。我們一直稱其為分佈，但是分佈的到底是什麼？我們可以直觀地認為機率分佈是一個任務中所有可能存在的事件及其對應的機率，例如在「拋硬幣」任務中，「正面」和「反面」兩個事件，以及它們對應出現的機率 1/2 可以組成一個分佈。

在機率中，正態分佈是所有事件及對應機率的特定分佈。x 軸表示我們想知道機率的事件，y 軸是與每個事件相關聯的機率——從 0-1。在這裡，我們沒有深入討論機率分佈，但是知道正態分佈是一種特別重要的機率分佈。

在統計中，正態分佈是資料值的分佈。在這裡，x 軸是資料的值，y 軸是這些值的計數。以下是兩張相同的正態分佈圖，但是根據機率和統計來進行標記：

在機率的正態分佈中，最高點表示發生機率最大的事件。離這個事件越遠，機率下降越厲害，最後形成一個鐘的形狀。而在統計的正態分佈中，最高點代表均值，與機率中的情況類似，離均值越遠，頻率下降越厲害。也就是說，兩端的點與均值存在極高的偏差，且樣本非常罕見。

如果你透過正態分佈懷疑機率和統計之間存在另一種關係，那麼你沒猜錯！我們將在本文後面探討這種重要關係，先彆著急。

既然打算用質量分數的分佈來比較不同的葡萄酒，我們需要設定一些條件來搜尋感興趣的葡萄酒。我們將收集葡萄酒的資料，然後分離出一些感興趣的葡萄酒質量分數。

為了取得資料，我們需要以下程式碼：

import csv
with open("wine-data.csv", "r", encoding="latin-1") as f:
    wines = list(csv.reader(f))

資料以表格形式顯示在下麵。我們需要 points 列，所以我們將把它提取到自己的串列中。一位葡萄酒專家告訴我們匈牙利的託卡伊白葡萄酒非常棒，而一位朋友則建議我們以義大利的藍布魯斯科紅葡萄酒開始入手。我們可以用資料來比較這些葡萄酒！

如果你不記得資料是什麼樣子的，下麵有一個簡要的表格供你參考和重新瞭解。

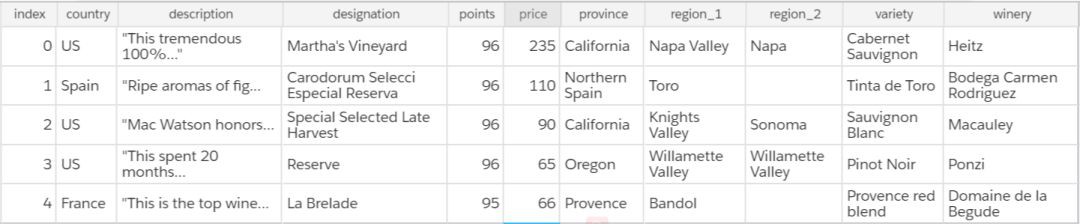
# Extract the Tokaji scores
tokaji = []
non_tokaji = []
for wine in wines:
    if points != '':
        points = wine[4]
    if wine[9] == "Tokaji":
        tokaji.append(float(points))
    else:
        non_tokaji.append(points)

# Extract the Lambrusco scores 
lambrusco = []
non_lambrusco = []
for wine in wines:
    if points != '':
        points = wine[4]
    if wine[9] == "Lambrusco":
        lambrusco.append(float(points))
    else:
        non_lambrusco.append(float(points))

如果把每組質量分數視覺化為正態分佈，我們可以根據它們所處的位置立即判斷兩種分佈是否相同，但如下所示用這種方法很快會遇到問題。因為我們有大量資料，所以假設分數會呈正態分佈。雖然這種假設在這裡沒問題，但實際上這麼做很危險，這點將在稍後討論。

當兩個分數分佈重疊太多時，最好假設你的分數是來自同一個而非不同的分佈。在另一種極端即兩個分佈沒有重疊的情況下，可以安全地假設它們來自不同的分佈。麻煩在於有些重疊的情況比較特殊。例如，一個分佈的極高點可能與另一個分佈的極低點相交，這種情況下我們該如何判斷這些分數是否來自不同的分佈。

因此，我們再次期望正態分佈可以給我們一個答案，併在統計學和機率之間架起一座橋梁。

04 重新審視正態分佈

正態分佈對機率和統計學來說至關重要，原因有二：中心極限定理和 3σ 準則。

1. 中心極限定理

在上一節中，我們展示瞭如果把擲硬幣的試驗重覆十次，正面朝上的平均結果將接近理想的 50%。隨著試驗次數的增加，平均結果會越接近真實機率，即使個別試驗本身並不完美。這種想法或數學上稱為依概收斂就是中心極限定理的一個關鍵原則。

在擲硬幣的例子中，一次試驗扔 10 次硬幣，我們會估計每次試驗正面朝上的次數為 5。之所以是估計，是因為我們知道結果並沒有那麼完美（即，不會每次都得到 5 次正面朝上的結果）。如果我們做出很多估計，根據中心極限定理，這些估計的分佈將看起來像正態分佈，這種分佈的頂點或估計值的期望將與真實值一致。我們觀察到，在統計學中正態分佈的頂點與平均值一致。因此，給定多次「試驗」作為資料，中心極限定理表明，即使我們不知道真正的機率，我們也可以透過資料估計出分佈可能的形狀。

中心極限定理讓我們知道多次試驗的平均值將接近真實平均值，而 3σ準則將告訴我們有多少資料將圍繞這個平均值分佈。

2. 3σ 準則

3σ 準則（也被稱為經驗法則或 68-95-99.7 法則），是我們觀察到有多少資料落在平均值某一距離內的一種表達。註意，標準差（又名「sigma」）是資料觀測值與平均值之間的平均距離。

3σ 準則規定，給定正態分佈，68% 的觀測值將落在平均值的一個標準差之間，95% 將落在兩個標準差以內，99.7% 將落在三個標準差以內。很多複雜的數學都涉及這些值的推導，因此，具體不在本文的討論範圍之內。關鍵是要知道，3σ 準則使我們能夠瞭解正態分佈的不同區間內分別包含了多少資料。下圖是對 3σ 準則所代表內容的總結。

我們將把這些概念與葡萄酒資料聯絡起來。根據假設，作為一個品酒師，我們想知道與普通葡萄酒相比，霞多麗白葡萄酒和黑皮諾葡萄酒更受歡迎的程度。我們收集了成千上萬條關於葡萄酒的評論，而根據中心極限定理，這些評論的平均分數應該與葡萄酒質量（由評論者判斷）的「真實」表徵一致。

雖然 3σ 準則說明瞭你的資料有多少在已知值範圍內，但它也說明瞭極端值的罕見性。任何偏離平均值三個標準差的值都應小心處理。透過 3σ準則和 Z-score，我們最終可以透過數值度量霞多麗白葡萄酒、黑皮諾葡萄酒與普通葡萄酒的區別程度。

05 Z-score

Z-score 是一個簡單的計算，它回答了這樣一個問題：「給定一個資料點，它離平均值有多少標準差？」下麵是 Z-score 方程：

Z-score 本身並沒有給你提供很多少資訊。但當與一個 Z-table 比較時，它就非常有價值，該表列出了一個標準正態分佈的累積機率，直到給定 Z-score。標準正態分佈是平均值為 0、標準差為 1 的正態分佈。即使我們的正態分佈不是標準的，Z-score 也允許我們參考 Z-table。

累積機率（或稱為機率分佈函式）是給定點出現之前所有值的機率之和。一個簡單的例子是平均值本身。平均值是正態分佈的正中間部分，所以我們知道從左向右取值到平均值的所有機率之和為 50%。如果你想計算標準差之間的累計機率，3σ準則的值實際上會出現。下圖是累積機率的視覺化圖。

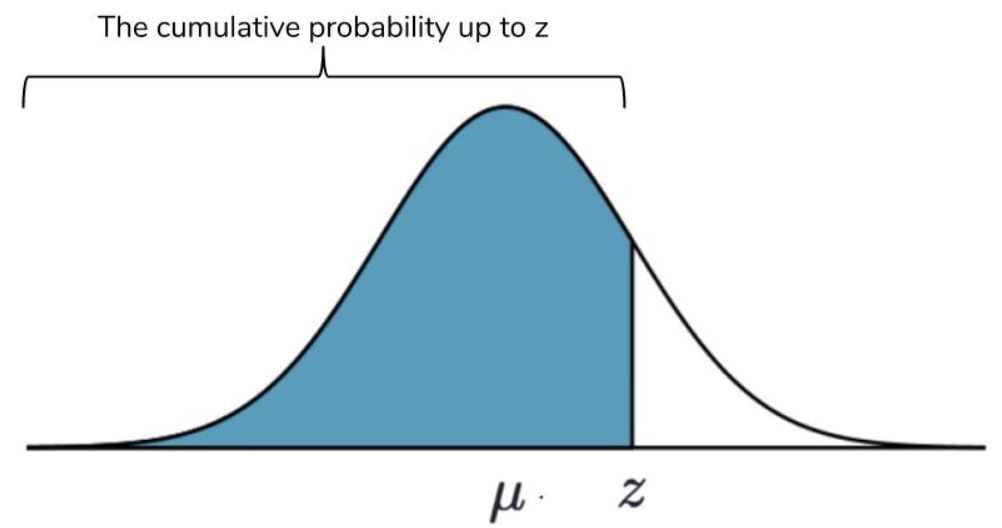
所有機率之和必須等於 100%，所以我們用 Z-table 來計算正態分佈下 Z-score 兩邊的機率。

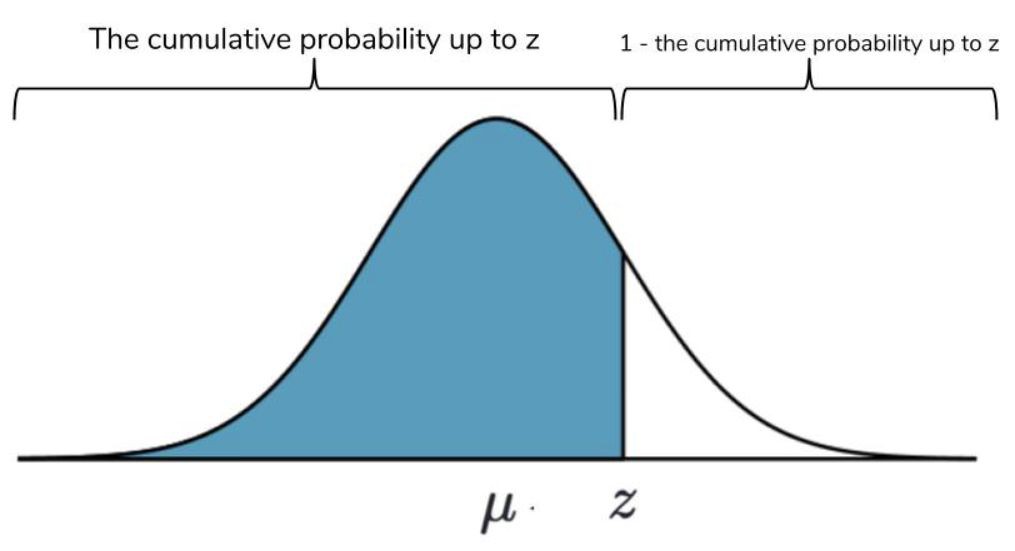
這種超過某個 Z-score 的機率計算對我們很有用。它讓我們從「一個值離平均值有多遠？」的問題升級到「一個值與同一組觀測值的平均值相差特定距離的可能性有多大？」因此，從 Z-score 和 Z-table 得出的機率將回答我們關於葡萄酒的問題。

import numpy as np
tokaji_avg = np.average(tokaji)
lambrusco_avg = np.average(lambrusco)

tokaji_std = np.std(tokaji)
lambrusco = np.std(lambrusco)

# Let's see what the results are
print("Tokaji: ", tokaji_avg, tokaji_std)
print("Lambrusco: ", lambrusco_avg, lambrusco_std)
>>> Tokaji:  90.9 2.65015722804
>>> Lambrusco:  84.4047619048 1.61922267961

看起來朋友的推薦並不是很好！為了本文的目的，我們把託卡伊白葡萄酒和藍布魯斯科紅葡萄酒的分數都視為正態分佈。因此，每種葡萄酒的平均分數將代表它們在質量方面的「真實」分數。我們將計算 Z-score，看看託卡伊白葡萄酒的平均值與藍布魯斯科紅葡萄酒的平均值相差多少。

z = (tokaji_avg - lambrusco_avg) / lambrusco_std
>>> 4.0113309781438229

# We'll bring in scipy to do the calculation of probability from the Z-table
import scipy.stats as st
st.norm.cdf(z)
>>> 0.99996981130231266

# We need the probability from the right side, so we'll flip it!
1 - st.norm.cdf(z)
>>> 3.0188697687338895e-05

答案是差距很小。但這到底意味著什麼？這種機率的無窮小量可能需要詳細解釋。

假設託卡伊白葡萄酒和藍布魯斯科紅葡萄酒的質量沒有什麼差別。也就是說，二者的品質差不多。同樣，由於葡萄酒之間的個體差異，這些葡萄酒的分數會有一些分散。根據中心極限定理，如果我們製作這兩種葡萄酒分數的直方圖，將會產生服從正態分佈的質量分數。

現在，我們可以利用一些資料計算出這兩種葡萄酒的平均值和標準差。這些值可以檢驗它們的品質是否相似。我們將使用藍布魯斯科紅葡萄酒分數作為基礎，並比較了託卡伊白葡萄酒的平均分數，反過來做也很簡單。唯一不同的是負 Z-score。

Z-score 為 4.01！假設託卡伊和藍布魯斯科的品質相似，根據 3σ準則，99.7% 的資料應該在 3 個標準差範圍內。在託卡伊和藍布魯斯科被視為品質相同的情況下，遠離質量分數平均值的機率非常非常小。這種機率如此之小，以至於我們不得不考慮相反的情況：如果託卡伊不同於藍布魯斯科，將會產生不同的分數分佈。

此處我們仔細選擇了措辭：我沒有說「託卡伊比藍布魯斯科好」。因為我們計算了這種機率，雖然微觀上很小，但不是零。確切地，可以說託卡伊和藍布魯斯科絕對不是來自同一個分佈，但不能就此說其中一種比另一種更好或更差。

這種推理屬於推理統計的範疇，而本文只想做一個簡單的介紹。本文介紹了很多概念，所以如果你覺得有些頭疼，不妨回頭慢慢看。

06 總結

我們從描述性統計開始，然後將其與機率聯絡起來。根據機率，我們開發了一種定量顯示兩組分數是否來自同一分佈的方法。根據這種方法，我們比較了別人推薦的兩種葡萄酒，發現它們很可能來自不相同的質量分數分佈。也就是說，一種葡萄酒很可能比另一種更好。

統計不是隻屬於統計學家的領域，作為一名資料科學家，對常用的統計方法有一個直觀的理解將有助於你構建自己的理論，以及隨後測試這些理論的能力。在這裡我們幾乎沒有觸及推理統計，但是同樣的想法將有助於指導理解統計原理。本文討論了正態分佈的優點，但是統計學家也開發了非正態分佈的技術。

原文連結：

https://www.dataquest.io/blog/basic-statistics-in-python-probability/