漫畫：什麼是二叉堆？

————————————

什麼是二叉堆？

二叉堆本質上是一種完全二叉樹，它分為兩個型別：

1.最大堆

2.最小堆

什麼是最大堆呢？最大堆任何一個父節點的值，都大於等於它左右孩子節點的值。

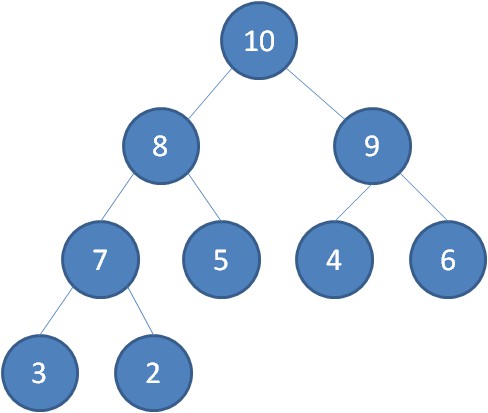
什麼是最小堆呢？最小堆任何一個父節點的值，都小於等於它左右孩子節點的值。

二叉堆的根節點叫做堆頂。

最大堆和最小堆的特點，決定了在最大堆的堆頂是整個堆中的最大元素；最小堆的堆頂是整個堆中的最小元素。

堆的自我調整

對於二叉堆，如下有幾種操作：

插入節點

刪除節點

構建二叉堆

這幾種操作都是基於堆的自我調整。

下麵讓我們以最小堆為例，看一看二叉堆是如何進行自我調整的。

1.插入節點

二叉堆的節點插入，插入位置是完全二叉樹的最後一個位置。比如我們插入一個新節點，值是 0。

這時候，我們讓節點0的它的父節點5做比較，如果0小於5，則讓新節點“上浮”，和父節點交換位置。

繼續用節點0和父節點3做比較，如果0小於3，則讓新節點繼續“上浮”。

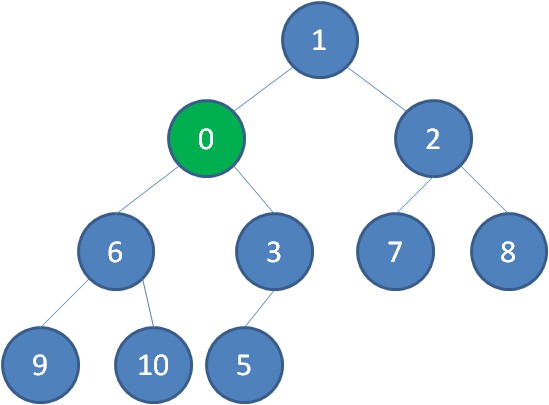
繼續比較，最終讓新節點0上浮到了堆頂位置。

2.刪除節點

二叉堆的節點刪除過程和插入過程正好相反，所刪除的是處於堆頂的節點。比如我們刪除最小堆的堆頂節點1。

這時候，為了維持完全二叉樹的結構，我們把堆的最後一個節點10補到原本堆頂的位置。

接下來我們讓移動到堆頂的節點10和它的左右孩子進行比較，如果左右孩子中最小的一個（顯然是節點2）比節點10小，那麼讓節點10“下沉”。

繼續讓節點10和它的左右孩子做比較，左右孩子中最小的是節點7，由於10大於7，讓節點10繼續“下沉”。

這樣一來，二叉堆重新得到了調整。

3.構建二叉堆

構建二叉堆，也就是把一個無序的完全二叉樹調整為二叉堆，本質上就是讓所有非葉子節點依次下沉。

我們舉一個無序完全二叉樹的例子：

首先，我們從最後一個非葉子節點開始，也就是從節點10開始。如果節點10大於它左右孩子中最小的一個，則節點10下沉。

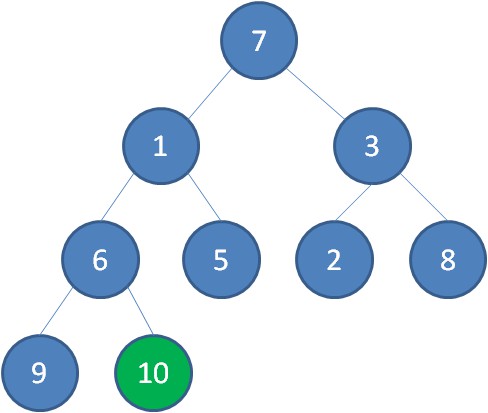
接下來輪到節點3，如果節點3大於它左右孩子中最小的一個，則節點3下沉。

接下來輪到節點1，如果節點1大於它左右孩子中最小的一個，則節點1下沉。事實上節點1小於它的左右孩子，所以不用改變。

接下來輪到節點7，如果節點7大於它左右孩子中最小的一個，則節點7下沉。

節點7繼續比較，繼續下沉。

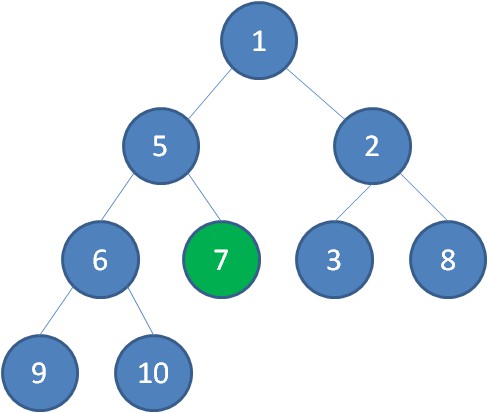
這樣一來，一顆無序的完全二叉樹就構建成了一個最小堆。

堆的程式碼實現

在擼程式碼之前，我們還需要明確一點：

二叉堆雖然是一顆完全二叉樹，但它的儲存方式並不是鏈式儲存，而是順序儲存。換句話說，二叉堆的所有節點都儲存在陣列當中。

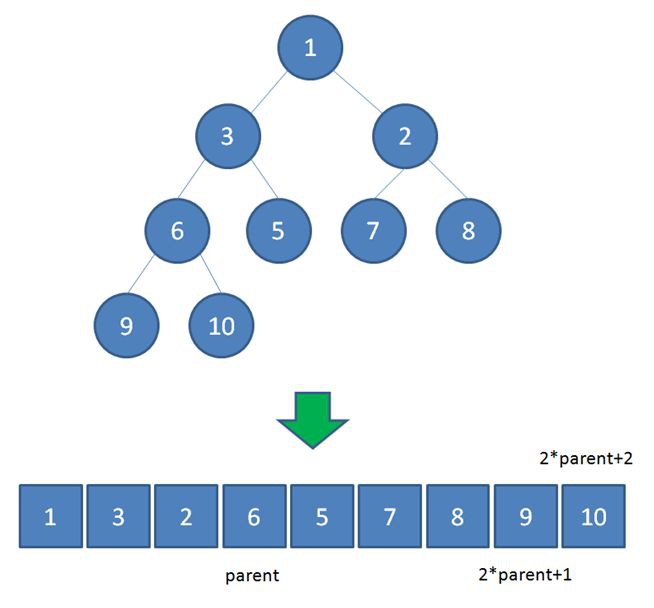
陣列中，在沒有左右指標的情況下，如何定位到一個父節點的左孩子和右孩子呢？

像圖中那樣，我們可以依靠陣列下標來計算。

假設父節點的下標是parent，那麼它的左孩子下標就是 2*parent+1；它的右孩子下標就是  2*parent+2 。

比如上面例子中，節點6包含9和10兩個孩子，節點6在陣列中的下標是3，節點9在陣列中的下標是7，節點10在陣列中的下標是8。

7 = 3*2+1

8 = 3*2+2

剛好符合規律。

有了這個前提，下麵的程式碼就更好理解了：

public class HeapOperator {

/**
 * 上浮調整
 * @param array     待調整的堆
 */
public static void upAdjust(int[] array) {
    int childIndex = array.length-1;
    int parentIndex = (childIndex-1)/2;
    // temp儲存插入的葉子節點值，用於最後的賦值
    int temp = array[childIndex];
    while (childIndex > 0 && temp < array[parentIndex])
    {
        //無需真正交換，單向賦值即可
        array[childIndex] = array[parentIndex];
        childIndex = parentIndex;
        parentIndex = (parentIndex-1) / 2;
    }
    array[childIndex] = temp;
}

/**
 * 下沉調整
 * @param array     待調整的堆
 * @param parentIndex    要下沉的父節點
 * @param parentIndex    堆的有效大小
 */
public static void downAdjust(int[] array, int parentIndex, int length) {
    // temp儲存父節點值，用於最後的賦值
    int temp = array[parentIndex];
    int childIndex = 2 * parentIndex + 1;
    while (childIndex < length) {
        // 如果有右孩子，且右孩子小於左孩子的值，則定位到右孩子
        if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
            childIndex++;
        }
        // 如果父節點小於任何一個孩子的值，直接跳出
        if (temp <= array[childIndex])
            break;
        //無需真正交換，單向賦值即可
        array[parentIndex] = array[childIndex];
        parentIndex = childIndex;
        childIndex = 2 * childIndex + 1;
    }
    array[parentIndex] = temp;
}

/**
 * 構建堆
 * @param array     待調整的堆
 */
public static void buildHeap(int[] array) {
    // 從最後一個非葉子節點開始，依次下沉調整
    for (int i = array.length / 2; i >= 0; i--) {
        downAdjust(array, i, array.length - 1);
    }
}

public static void main(String[] args) {
    int[] array = new int[] {1,3,2,6,5,7,8,9,10,0};
    upAdjust(array);
    System.out.println(Arrays.toString(array));
    array = new int[] {7,1,3,10,5,2,8,9,6};
    buildHeap(array);
    System.out.println(Arrays.toString(array));
}