機率入門：雙色球中獎、購車搖號中簽和德撲同花順，哪個更容易？

作者：高揚、衛崢、尹會生

插畫設計：萬娟

01 雙色球彩票

雙色球彩票在中國的歷史不算短了，大概是從2003年2月就開始在中國聯網發售。雖然有很多人都在詬病說雙色球開獎的方式不夠公平透明，但是還有相當多的彩民一直在執著地研究雙色球開獎的規律。

咱們今天只從數學的角度來看一下雙色球彩票的頭獎和你花兩塊錢下註購買的彩票一致性的機率，也就是我們平時說的買一註然後就能中頭獎的機率有多大。我們必須先明確一個前提，就是確實沒有人對彩票購買和抽獎小球的抽出做幹預，換而言之，就是你下註的這一註是在完全不知道開獎結果的情況下買的，抽獎也是每個球被抽出的機率一樣的情況下做的。

我們購買一註彩票的時候，首先選擇紅球，從01到33，共33個號碼中選擇6個號碼。再從01~16，共16個號碼中選擇1個號碼。6紅1藍一共7個號碼組成完整的一註彩票。

最終抽獎的時候也會是01~33個紅色號碼中選擇6個號碼，再從01~16，共16個藍色號碼中選擇1個號碼。6紅1藍一共7個號碼組成完整的一註頭獎彩票。

如果你選擇的6紅1藍和頭獎的6紅1藍完全一致那就算中了頭獎，獎金怎麼算……這個大家去問福利彩票中心吧，咱們這裡只算機率。

先算算我們挑選6紅1藍一共有多少種挑法。

首先先從33個紅球中挑選6個紅球，用組合的方式，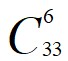

=33×32×31×30×29×28/(6×5×4×3×2×1)

=1107568

也就是1107568種選法。

再從16個藍色球中選1個，16種選法。

這樣6紅1藍的選法就是一共是1107568×16=17721088種選法。

說個形象點的例子，老天爺在想1到17721088中的一個整數，你也在想1到17721088中的一個整數，你們倆想的完全一樣的機率有多大？沒錯1/17721088，大約是0.0000000564%的機率。還能數的清有多少0麼？

不少人說，這沒關係，反正有一些破法。有哪些破法？看了一下有兩種支援的人比較多。

方法一：我多買幾種配置方法，換句話說，多想幾個數去跟老天爺碰運氣？

那就算算看，一共17721088種可能，全部買下來——也就是俗稱的全餐彩票，一共要花35442176元人民幣。獎池是不是在所有中頭獎的人平分後還能至少分到手這麼多不好說（包括加上二等、三等獎一共能領到多少錢都可以自己算）。我們按照比例縮小一些試試呢？比如買一半，那就是中獎機率變成1/2——要花掉17721088元，還有一半的可能性是不中。其他比例大家可以自己計算。每一種在降低投入的同時，也在降低中獎機率。所以這種方式並沒有提高買彩票的投入產出比。

方法二：我只買一種組合，堅持到底，就能提高勝率？

有這樣思想的朋友估計是這麼一個思路，就是說這一次這種組合不中，由於每種組合機率一樣，所以在多次隨機過程裡前面出現過的組合後面出現的機率就低，前面沒出現過的組合後面出現的機率就高。有這樣思路的朋友，想想這樣一個事，交通事故其實是一個典型的隨機事件。平均每個月發生交通事故的數量是相對“固定”的，只不過發生的地點，發生的時間，發生的車型，涉及到的人可能不同而已。

那麼如果要避免交通事故，那麼就先人為製造一些無害的交通事故就好了，造夠了次數，這個月就不會再發生交通事故了，大家也可以安心上路隨便開了。這個邏輯就變得順理成章，但是事實真的會是這樣嗎？

這種隨機產生的每一次結果之間其實是獨立的機率，換句話說每一次之間是不會影響前後隨機事件裡產生的結果的，也不會影響到前後的隨機事件的結果。在靜態概型裡，這個結論請大家牢記。

也有人表示懷疑，說我明明在一些事情裡看到前一件事發生後會影響後面事情發生的可能性，那這種事情怎麼解釋。這種事情，首先不是古典概型的範疇，如果要歸類的話可以算作條件機率的研究範疇，條件機率以後我們也會詳細講解。

02 購車搖號

北京是一個以擁堵著稱的城市，擁堵的問題也是由來已久，而且幾乎是越來越嚴重。在萬般無奈的情況下，專家們最後祭出了一個大招——搖號。

搖號是一個帶有比較濃鬱配給制色彩的手段。大概的形式就是，每個已經具備搖號資格的人登記一下身份證號碼，所有登記過身份證號碼的人都放在一個大“池子”裡，然後每兩個月透過“隨機”的方式產生20000個號碼，這20000個幸運兒就是中簽者，就擁有了購買一輛汽油動力汽車的配額。

中簽機率多大呢？有人想到直接用20000÷1420000就是自己中簽的機率。但是為什麼是這麼求呢？有理論依據嗎？我們試著推導一下。

以真實資料為例，2015年9月的時候這個“池子”裡一共有大約1420000個號，從裡面選出20000個號，一個人中簽的機率有多大？稍微想想看，這個數值也不能夠是。因為不是要求1420000個號裡找出20000個號一組的不同組合。

假如我參與了搖號，在沒有其他政策進行幹預而將1420000個號碼進行等機率選出的情況下，選出20000個號，而我的號正好在其中。相當於用一個1420000面的骰子，投擲一次，選出一個號，然後把這個號抹掉，再用剩餘的1419999個號做成一個1419999的骰子，再投擲一次，選出一個號，然後把這個號再抹掉……一次一次下去，直到20000次為止。實際相當於這麼一個過程。

想不清的話我們試試用小一點的數字找找感覺。

如果是有3個人參與搖號，搖出2個，是怎麼計算呢？

按照這種扔骰子的方法來玩，假設我們有個3面的骰子（其實真的是沒辦法做出一個3個面的等機率骰子，我們就當真的能做出來好了）。第一次我被骰子選中的機率為1/3，還有2/3是沒被選中的機率。在沒選中的情況下，換2個面的骰子，這一次我被骰子選中的機率為1/2。

算算我能被選中的機率一共是多少吧，1/3+(2/3)×(1/2)=2/3。

如果是6個人參與搖號，搖出3個，是怎麼計算呢？

仍然用扔骰子的方法來玩，同理：

• 第一次，選中的機率為1/6，沒選中的機率為5/6，現在該換5面的骰子了。

• 第二次，選中的機率為1/5，沒選中的機率為4/5，現在該換4面的骰子了。

• 第三次，選中的機率為1/4，沒選中的機率為3/4，結束。

被選中的機率是多少呢1/6+(5/6)×(1/5)+(4/5)×(1/4)=3/6。

如果有興趣可以繼續用其他例子去算，我們現在直接說結論了，這種情況其實就是用擲骰子的次數除以最開始骰子的總面數，也就是一共選出的次數除以全樣本空間的大小。20000/1420000這個答案是沒有問題的，也就是中簽率不過1.4%左右，一年搖號6次的話，估計運氣最差的人要11.8年才能抽中，聽到這樣的訊息現在整個人都不好了。不過別忘了，每個月這個“池子”還在變大，究竟等多久可能只有老天知道了。

03 德州撲克

七零後和八零後的朋友估計對香港影星周潤發很熟悉，尤其是發哥在《賭神》系列中風流倜儻的表演給人留下很深的印象，其中最後發哥和大BOSS單挑基本玩的都是“梭哈”——英文名稱Show Hand。梭哈和我們今天要說的德州撲克在牌點大小比較的規則上是非常近似的。

德州撲克是很多年輕人都喜歡的撲克競技遊戲，全稱是Texas Hold’em poker，中文簡稱德州撲克。我們今天就來研究一下各種牌型出現的機率如何。

對於不熟悉德州撲克規則的朋友來說，還是有必要先簡單描述一下德州撲克的規則。

一張臺面至少2人，最多22人，一般是由2~10人參加。德州撲克一共有52張牌，沒有王牌。每個玩家分兩張牌作為“底牌”，五張由荷官（就是專業發牌的）陸續朝上發出的公共牌。開始的時候，每個玩家會有兩張面朝下的底牌。經過所有押註圈後，若仍不能分出勝負，遊戲會進入“攤牌”階段，也就是讓所剩的玩家亮出各自的底牌以較高下，持大牌者獲勝。

• 第一輪是在每位玩家只能看到自己2張底牌的情況下加註。

• 第二輪是在每位玩家能看到自己2張底牌，以及桌面上3張公共牌的情況下加註。

• 第三輪是在每位玩家能看到自己2張底牌，以及桌面上4張公共牌的情況下加註。

• 第四輪是在每位玩家能看到自己2張底牌，以及桌面上5張公共牌的情況下加註。

最多隻會經歷這四輪，一局遊戲結束。

遊戲的輸贏就是看玩家自己的2張底牌與桌面上當前已開出的公共牌，一共挑選出5張，組成最“大”的牌，哪位玩家的牌組合最“大”，哪位玩家就獲得勝利。

牌的組合大小怎麼定義呢？

有些對博弈類遊戲有所瞭解的朋友可能會有一些常識性的體會——那就是，組合出現的可能性越小的通常牌越“大”。那德州撲克裡都有哪些組合呢？

第一等：同花大順

相同花色的A、K、Q、J、10。

第二等：同花順

相同花色的5張相連。例如，紅桃6、7、8、9、10；黑桃9、10、J、Q、K。

第三等：四條

4張相同點數的牌。例如，4張8；4張Q。

第四等：滿堂紅（也叫葫蘆）

3張相同點數的牌，再加2張相同點數的牌。例如，3張5和2張9；3張K和2張10。

第五等：同花

5張相同花色的牌，但不是同花順。例如，5張都是方塊；5張都是梅花。

第六等：順子

5張點數相連的牌，但至少包含兩種花色。例如，方塊2、方塊3、梅花4、紅桃5、紅桃6；紅桃8、方塊9、梅花10、紅桃J、黑桃Q。

第七等：三條

3張相同點數的牌，再加2張不同點數的牌。例如，3張9和1張3、1張K；3張Q和1張A，1張6。

第八等：兩對

2張相同點數的牌作為一對，兩對牌，再加1張單牌。例如，2張5、2張9、1張A；2張10、2張J、1張K。

第九等：一對

2張相同點數的牌作為一對，一對牌，再加3張單牌。例如，2張10、1張7、1張8、一張9；2張A、1張K、1張9、1張5。

第十等：高牌

高牌即單牌，不滿足前面九等牌中任何一種的，就只能按照點數大小按順序決定高低了。A比K大，K比Q大，以此類推，2最小。

我們在這裡就試求一下，一個人自己摸牌（沒有任何第二個玩家參與的情況下），前三等牌被摸到的機率有多大。

請註意一點，在沒有開始摸牌之前，如果牌被洗過若干次（沒有其他人為幹擾因素）的情況下，牌的發放是隨機的。而一旦底牌發放以後，尤其是玩家自己看過牌以後，這個時候的機率計算和我們現在要討論的這種機率計算是不一樣的——顯然，一個是完全隨機的，一個是有一定條件的，條件就是剛剛看到的那兩張底牌，而這種情況我們暫時不討論。

那麼這種情況下，整個選牌的過程中相當於從整副牌52張中選出7張，並從中組合出最大牌的過程，即

=52×51×50×49×48×47×46/(7×6×5×4×3×2×1)

=133784560

7張牌的組合一共有133784560種。

1. 同花大順

在所有的組閤中有多少是同花大順的呢？同花大順一共就4種，分別是黑桃、紅桃、梅花、方塊的10、J、Q、K、A。7張牌裡面，5張已經確定，另外兩張怎麼選都無所謂。以黑桃為例，黑桃的同花大順選出後，其實還有47張牌沒有發，挑出兩張即

=47×46/(2×1)=1081

同理，紅桃、梅花、方塊的同花大順也是一樣的，都是1081種組合。則同花大順共計有4324種組合。聽著挺多的是吧，別忘了一共133784560種組合，除一下得到結果

4324/133784560=0.00323%

2. 同花順

同花順有多少種情況呢？以黑桃為例，假設A~5組成同花順，黑桃6是不能發的，還剩下46張可以組合，則這種情況下組合數量這樣計算

=46×45/(2×1)=1035

2~6組成同花順，7是不能發的，A可以發（A充作散牌），所以還是

=1035

以此類推，黑桃的組合為A~5，2~6……9~K，一共9種，那麼黑桃一種花色的牌型種類就為

1035×9=9315

四種花色的組合數就是

9315×4=37260

除一下得到結果機率

37260/133784560=0.0279%

網上還有一種演演算法說是

38916/133784560=0.0291%

這種演演算法是有問題的。錯誤發生的地方大概在這裡：“以黑桃為例，A~5，2~6……9~K，一共9種，47張裡挑出兩張，計算一下

=47×46/(2×1)=1081

那麼黑桃的同花順的牌型一共是

1081×9=9729

同理，紅桃、梅花、方塊的同花順也是一樣的，都是9729種組合，共計38916種組合，除一下得到結果

38916/133784560=0.0291%

這裡一旦選好了5張牌作為“核心組合”以後，其他牌的選擇其實不是自由的，因為有的牌配進來以後就發現這個我們一開始就認定的組合不是最後在臺面上最大的牌。這個地方需要註意一下。

3. 四條

四條有多少種呢，計算方法類同，4張已經確定，還有48張沒有發

=48×47×46/(3×2×1)=17296

註意這裡4張的組合有多少種——13種，所以四條可能出現的組合數量為

17296×13=224848

除一下得到結果

224848/133784560=0.168%

雖然看上去機會仍然很渺茫，但是比同花大順和同花順的機率還是大了不少是不是？

其他的組合方式大家有興趣可以自己慢慢去算，網上也有現成算好的對照表。

提示一下，像兩對牌這種的比較難算，因為情況比較複雜。它複雜的地方在於在滿足兩對牌的情況下，還要將滿足同花大順、同花順、四條、滿堂紅、同花、順子、三條的情況全部剔除才行。兩對牌的牌型為31433400種，機率為23.5%。還有一些其他形式的對照表，就是在手裡底牌為已知固定組合的情況下，最終與公共牌組合成為各等牌的機率。

這裡溫馨提醒一下各位牌友，剛剛我們計算的機率是在一個人自己摸牌的情況下產生的機率。一旦是5個人，10個人玩的時候就大不相同了，有一點是確定的，人越多公共牌和其他玩家一起組成的牌的種類可能性也越多，“罕見組合”在一局中出現的可能性也比一個人自己摸牌要高很多，請一定註意哦。

• 6年級學Python，高中學AI？這6本書，助你找回輸掉的起跑線

• 終於有人把資料、資訊、演演算法、統計、機率和資料挖掘都講明白了！

• 以朋友圈為例，騰訊資深架構師揭秘鵝廠大資料平臺是怎樣運營的

• 上清華到底有多難？清華大學保送生的數學試題瞭解一下