揭露: SSD寫頻寬保持恆穩的秘密

經過慎重考慮，他把驗證“商業樣式”的地點選擇在了雷偌市。索普一戰成名，僅僅用了一個週末，就把天使投資額翻了一番。這個訊息後來橫掃博 彩社群，隨後，索普寫了《戰勝莊家》。

大峽谷，胡佛大壩，米德湖等奇特的自然風光勾勒出了這個城市的一面，而令人深陷其中不由貪戀的紙醉金迷般的城市風情則代表了它的另外一面。拉斯維加斯，這座位於沙漠之中的繁華城市，是一座以賭博業為中心的旅遊、購物、度假的世界知名度假城市，擁有“世界娛樂之都”和“結婚之都”的美稱。

拉加維加斯大道是這座沙漠之城繁華的開始，是不夜城的中心，也是最繁華的地帶。街區兩旁是無比奢華的酒店、熱鬧非凡的賭場。還有各種埃及金字塔、埃菲爾鐵塔、自由女神像這樣的世界奇跡的縮影讓你目不暇接。走在熙熙攘攘的街道，你可以看熱情奔放的金髮女郎，呼嘯而過的豪車。

拉斯維加斯的主要經濟支柱是博 彩業，在大道街上有高階的旅館賭場和秀場。不少遊客本著獵奇的態度，走進這個虛幻的世界。而賭場則利用對於人性地把握，讓賭客在享受到視聽盛宴服務的同時，心甘情願的把自己的錢投入到一個個賭局當中。而賭場贏錢的秘密，則在於利用人性的特點設計不公平的賭局。即便是看似“公平”的賭博，實際上也會最終讓賭客輸得精光。在這個奧秘的背後，起作用的是機率學的客觀規律。

機率學在長久的發展中為我們提供了許多有趣的定理，其中就有那麼一條賭徒輸光定理。根據賭徒輸光定理，在“公平”的賭博中，任一個擁有有限賭本的賭徒，只要長期賭下去，必然有一天會輸光。在一次賭博中，任意一個賭徒都有可能會贏，誰輸誰贏是偶然的。但只要一直賭下去，輸光或者莊家破產跑路是必然的。然而確實有人曾經利用數學知識打敗了莊家，並取得了“賭博教父”的稱號。

他就是文章開頭故事中《戰勝莊家》的作者——愛德華·索普。索普透過他的21點制勝理論，一戰成名。一時間，坊間巷裡流傳著這樣的故事：有個人“奇襲”了內華達雷偌市的所有賭場，併成功地從“21點”桌上贏了數萬美元。那些曾經遭遇橫掃的賭場，紛紛將其拉入黑名單，併合謀更改遊戲規則……索普還間接推動了期權定價模型的發展，最終導致著名的Black Scholes期權定價模型的誕生。

時間退回至 1905 年，年僅 26 歲的愛因斯坦還在瑞士伯爾尼專利局任三級技術員，這一年他似乎突然天才迸發，連續發表了 4 篇引發科學革命的論文。其中有關光電效應，質能等效性和狹義相對論的3篇論文為世人熟知，還有一篇是有關布朗運動的。

在這篇論文中，愛因斯坦指出：在空間中，如果一個質點在時刻 0 位於原點，每過單位時間該質點從當前位置沿隨機方向移動單位距離到一個新的位置，那麼這個質點的運動服從布朗運動，並且在時刻n它到原點的距離的平均值滿足。

我們把這個結論例化到一維的情況。假設一個賭徒參加一個公平的賭局，他每次有一半的機率贏 1 元，一半的機率輸 1 元。這樣 n 次以後，他的籌碼數量變化的期望值為，這說明隨著時間增加，賭徒手裡的籌碼數量相比初始籌碼數量的差值將會越來越大。最終或者賭徒贏到足夠多的錢不再繼續賭下去，或者是輸光了黯然離場。然而根據賭徒輸光定理，很有可能出現的是後一場景。

為了說明這個結論，假定賭徒手裡初始有r元，且賭徒一直不停賭博直到輸光為止，我們嘗試求解輸光的次數小於 n 的機率 p(r,n) 。由於每次最多輸 1 元，因此至少需要 r 次，才能出現輸光的情況。當的時候，每次或者贏 1 元，或者輸 1 元，因此只有當 n-r  為偶數的情況，才會出現恰好輸光的情況。因此

採用古典機率公式，為了求解 n-r 為非負偶數時的 p(r,n) ，設 n-r=2m ，我們把所有的可能情況分成三種：

容易知道  。下麵分別計算和。為了計算E2事件的次數  ，考慮下麵 r=4 , n=10 的情況，從原點 Origin 到終點 Destination 有不同的路徑（圖中以實線表示）。使用者每一步從網格中的一個頂點向右上或者右下到下一個定點。由於 E2 表示在第 n 步，賭徒恰好輸光，所以在往右上或者右下進行行走的過程中不能與 y=0 這條虛線相交。最後一步恰好從坐標點 (9,1) 進入到 (10,0) 滿足恰好輸光。

為了求解  ，把它轉化成從原點 Origin 到終點Destination，並透過坐標點 (n-1, 1) 的所有的路徑數c₁減去與y=0這條線相交的路徑數 c₂，即  。前者容易計算為。為了計算後者，我們考慮所有與 y=0 這條線相交，並且至少有一處相交後往右上的方向行走。

當m>0的時候，利用映象原理，把這處往右上行走的步驟改為往右下行走，那麼最終結束的位置將會是坐標點 Destination’ (9,-1) 。容易證明採用上述做法進行映象的路徑與那些與 y=0 這條線相交的路徑一一對應，因此  ，如下圖所示。

而一旦知道了 ， 可以把各種在n時刻前已經輸光的情況合併計算得到：

綜合起來（定義  ），

我們把不同 r 對應的 p(r,n) 放到同一個圖中進行比較。它形象地揭示了賭徒輸光定理的含義，顯然“公平”賭博並不公平。從結果上看，隨著 n 的增加，賭徒輸光的機率會逐漸增加並趨近於 1 ，並且r越小，這種趨勢越明顯。這說明在公平賭博的情況下，擁有籌碼最少的賭徒會更容易破產。

對於一個理性的玩家賭徒， 必須試圖在每次賭局具有高於一半的勝算，這種賭博才是有收益的。我們修改一下上述問題，每次賭博的勝率是 α ，失敗機率是 β=1-α 。在 α>0.5 的情況下，每次收益的期望值是正數，因此可以預期這個賭博遊戲會源源不斷的盈利。事實的真相是這樣的嗎？

由於每次賭博都具有隨機性，雖然每次的期望值是正數，但是還是有一定可能性會出現輸光離場的情況。不過，隨著賭徒逐漸贏的錢逐漸增加，這種機率會越來越小。為了定量說明這種情況，考慮這樣一個不斷賭博的過程，設隨機變數T_r代表賭徒輸光離場的時間，Ts代表賭徒一旦贏了s元之後就決定離場的時間。設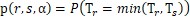代表賭徒因為輸光而離場的機率。考慮每次賭博勝率是α，失敗的機率是β，那麼可知

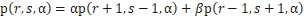
這個式子是二階線性差分方程，帶入初值p(0,s,α)=1，p(r,0,α)=0，可以得到

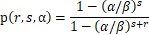
為了討論賭徒輸光的機率，令，得到。我們也把不同的r對應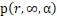畫出來。從結果上看，如果希望輸光的機率比較小，那麼需要每次的贏面足夠大或者是手裡的籌碼足夠多。對於如果α接近0.5，為了保持持續盈利，必須手裡籌碼足夠多才可行。

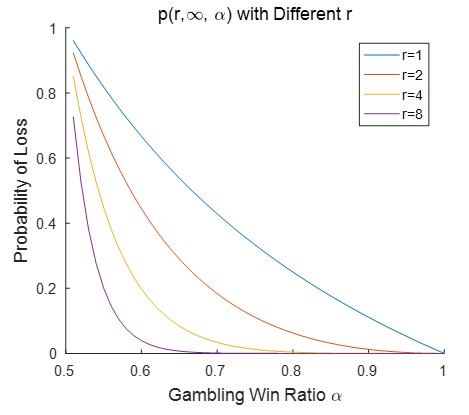
如果初始資金是r，但是每次賭註是2元，那麼輸光的機率又是多少呢？容易知道，這等價於初始資金是r/2和每次賭註是1元的情況。在這種情況下，雖然每次的期望贏錢數量翻倍了，但是輸光的機率確是按照平方根方式增加了。在r不高的情況下輸光的機率會大大增加。

我們已經從賭徒輸光定理談到了愛因斯坦的論文，有了這些知識的準備，我們現在來看看SSD中的垃圾回收。

通常 Victim Block 的選擇採用貪心演演算法，即選擇有最少資料的資料塊。也會適當考慮其他因素，例如在 “Design Tradeoffs for SSD Performance” 這篇論文中提到的基於時間的淘汰演演算法，適當考慮了冷資料並最佳化磨損均衡。

在下麵的圖中，選擇出來的Victim Block中有效資料比例為 v ，那麼 SSD 會把有效資料逐步從 Victim Block 中讀出來並且寫入到新的位置。同時會節約出來 1-v 對應的 Block 的空間，這個空間可以用來寫入使用者資料。在這個過程中，設 q 代表 GC 寫入數量與總寫入數量的比值，如果保持 GC 寫入數量佔比 q=v ，那麼使得GC回收完成一個 Block 的時候，剛剛好把新使用的 Block 相同大小的空間釋放出來，從而維持了OP資源不變，實現了垃圾回收的持續進行。若 q=v ，則對應的寫放大為 1/(1-v) 。在SSD的實現中，可以實現一個靈活調整使用者寫入資料的強度和GC的強度的流控機制，來實現 q=v 的標的。

但是，上述的過程實際上是一個過於理想化的過程。這是因為：

為瞭解決上述問題，需要在系統中預留一部分空閑的 Block 資源，當不同的 Victim Block 的有效資料發生波動的時候，這些資源可以用來補償和平滑這部分波動。這樣使得垃圾回收的強度不會隨著v而劇烈抖動，以及 SSD 表現出來的效能儘量平穩，避免OP 資源耗盡從而 SSD 無法進行垃圾回收。

設這部分資源的數量為r，那麼問題來了，到底r是多大合適？如果r較小，在r一旦耗盡，正常的垃圾回收就無法進行，導致嚴重後果；反之，過大的r則會浪費寶貴的OP，引起寫放大的增加。此外，在一定的r的前提下，到底如何選擇q，才能在波動性和安全性之間找到平衡點？如果採用保守的策略，可以選擇大一些的q，可以避免耗盡資源但同時會導致更大的波動；反之更加激進策略則會導致資源耗盡的機率增加，從而造成嚴重的問題。實際上，上述關於賭徒策略的分析可以幫助我們更好地理解這個問題。

“賭徒”SSD與“莊家”I/O請求的博弈

一旦莊家知道了這些SSD的底牌，莊家則可以有針對性地向特定位置傳送寫請求，使得這些Block中含有有效資料的分佈呈現更加複雜的態勢，這會導致SSD選擇Victim Block更加困難和波動更大。莊家甚至可以“惡意地”幹擾磨損均衡過程，造成SSD內部的Block壽命分佈呈現擴大化趨勢。

所幸的是，莊家並不完全知道SSD內部Block中有效資料分佈的狀態。對於SSD來說，IO 業務並不是完全對立的關係。因此，我們可以假定這個“莊家”是善意的。這種善意最好的表示就是假設雖然Victim Block的有效資料量v存在波動，呈現一定的隨機性，但是同時v仍然滿足一定的分佈，可以用一個機率分佈函式來表示。進一步地，可以假設 v 服從  的正態分佈。為了儘量保持垃圾回收的速度不變，我們保持 q 在一段時間裡是常量。為了說明r隨時間變化的規律，我們引入連續時間的布朗運動，即維納過程。

數學中，維納過程是一種連續時間隨機過程。如果t>s，那麼維納過程要求在時刻t的位置 W_t 和s時刻的位置 W_s 滿足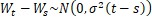。在上述SSD進行垃圾回收的模型中，如果設垃圾回收的相對比例q=μ,那麼r隨Victim Block的回收過程近似滿足維納過程即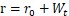。由於 W_t 在任意時刻均值為零，所以r的均值也不會變化，但是r的方差會隨時間逐漸變大。

可以類比賭徒輸光定理，採用上述的方案，在q=μ的情況下，如果時間足夠長，r 耗盡的機率趨近於 1，也就是說如果垃圾回收的速度等於平均的有效資料的比例的情況下，只要時間足夠長，總是會遇到空閑塊資源r耗盡的情況。因此必須使 q>μ ,才能使得系統在長時間足夠安全。在這種情況下  是一個上鞅。取用 “Adventures in stochastic processes” 中有關上鞅停時的結論，這種情況下長時執行導致r耗盡的機率為

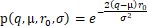
根據上述公式，在v的分佈  不變的情況下，空閑塊資源 r₀ 多，那麼系統安全性越高。為了保證一定的機率 p 下對應的 q，可以把上述公式求解q的運算式為

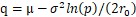
這個式子解釋了在一定的r資源耗盡機率下，資源數r，v的分佈引數 μ 和 σ² 與當前預期的垃圾回收比例之間的函式關係。由於 p<1 ，從而 q>μ ，說明在進行垃圾回收的時候由於 Victim Block 中有效資料量的抖動，必須保證垃圾回收速度要略微快於有效資源數的均值 μ ，才能實現比較安全的垃圾回收。在進行決策的時候，是根據當前可用的資源數r而不是 r₀ 來進行控制的。

與此同時，由於 q>μ ，採用上面的方式有可能會導致潛在資源數量r發散的情況。這會導致預留的空閑資源侵佔 OP 的空間。為瞭解決這個問題，可以設定一個資源數量的上限 r_m 。並且同樣利用上述方法構造一個下鞅限制系統以大機率不會出現資源數超出上限的情況。綜合上下界之後的公式為

我們比較和模擬了三種不同的情況。

針對三種情況，設定相同的 p ，μ  和σ²並模擬資源數r隨時間的變化和相對IOPS（定義成使用者寫入頻寬佔後端寫入總頻寬的比例，等於 1-q ）隨時間的變化規律。模擬結果如下圖所示。從結果可以看出，後兩種方法有效實現了系統的資源數r控制到了 0 到 r_m  這 r 個區間範圍內。

同時可以看到，採用固定 q=v 的控制方法會使得 IOPS 抖動很厲害。而採用資源池緩衝的方法，會讓 IOPS 顯得平滑。另外 r_m 越大， IOPS 的波動越小。因此，採用上述方法控制後，SSD 是有信心贏得這場賭局的，即採用一定量的空閑 Block 資源池來提升系統的 IOPS 寫入的穩定性。

為了進一步分析這個過程，我們把 r 和 q 的計算公式寫成迭代公式：

上面的迭代公式表明，r_n ，q_n 僅與r_n-1，q_n-1 有關，這符合馬爾可夫過程。因此，r_n ，q_n構成了連續狀態的馬爾可夫鏈。我們可以透過MCMC方法來估算它的穩態分佈，進而研究不同的引數對於系統的穩定性的影響。當 σ² 足夠小和r_m足夠大情況下，進行近似後，可以得到q的方差滿足下麵的關係。

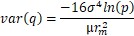
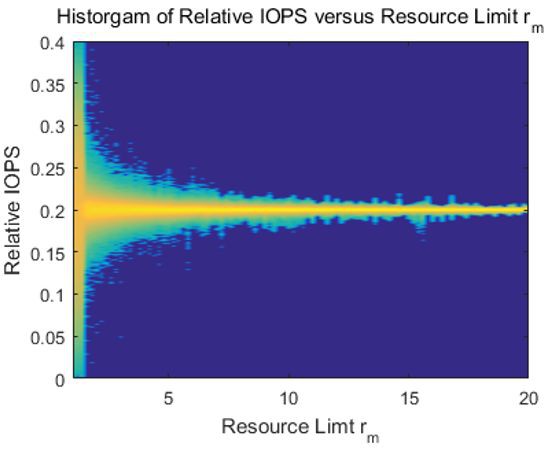
我們把不同的引數 p 下，相對的 IOPS 的分佈機率密度直方圖畫出來。從圖中可以看出來，當p比較小的時候，由於這一項計算出來的絕對值比較大，因此係統控制的相對比較保守。如果出現r偏移中心值較大的情況，會非常靈敏地調整IOPS以穩定r，因此相對的IOPS分佈的比較寬（在圖中反映的是對應的機率下黃色部分的高度較高）。

隨著p逐漸增加，IOPS的分佈會逐漸收窄，這說明我們適當放寬約束，可以使得相對的IOPS更加穩定，這與上述理論計算結果吻合。不過當p增加到10^-3的時候，可以看到IOPS的分佈會突然變寬。這是因為隨著控制策略的逐漸鬆弛，會有越來越大的機率出現r接近於 0 或者是 r_m 的情況。一旦出現這種情況，就會導致控制策略的強烈反應。這會使得 IOPS 不得不儘量考慮保證 r 不會超限，從而犧牲IOPS的穩定性。因此p的選擇決定了短期波動和長期波動的平衡。p選的比較大有助於保證短時間內的抖動較小，但是卻可能會影響到r的變化趨勢，造成長期波動的增加。因此要根據實際情況來進行選擇。

此外，固定p，改變 r_m 也可以理解空閑Block的數量對於IOPS抖動性的影響。這個所反應的規律與直覺是一致的，即隨著 r_m 的增加，IOPS的抖動性呈現反比關係下降的規律，這與上述公式反應的q的方差與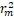呈反比例關係的規律一致。因此在條件允許的情況下，可以適當增加一些空閑塊資源用於平滑IOPS的波動。

在上面的分析中，透過對於 Victim Block 的建模，透過估算Victim Block短時分佈規律，我們從上得出了一個可信的垃圾回收穩定性方法，這個方法會對於SSD整體的寫入頻寬的平穩起到重要作用。實際情況中，對於 μ 和 σ² 需要有一個估計的過程，需要平衡估計的準確度和估計的跟蹤速度之間的關係。

把這個方法推廣開來，採用有效的方法來預測未來長時的垃圾回收效率，可以不僅僅保證短期的穩定性，也可以保證在 IO 業務發生劇烈變化的時候SSD的垃圾回收儘量符合預期和平穩化，限於篇幅關係這裡不再展開論述。

作者：路向峰