

超級計算機的一個必要元件是儲存系統。小型超算用到的資料較少,磁碟陣列就夠了,而大中型超算就要配備容量巨大的分散式儲存系統。
分散式儲存中經常遇到糾刪碼的概念:當冗餘級別為n+m時,從n個源資料塊中計算出m個的校驗塊,將這n+m個資料塊分別存放在n+m個硬碟上,就能容忍任意m個硬碟故障;硬碟故障時,只需任意選取n個正常的資料塊就能計算得到所有的源資料。如果將n+m個資料塊分散在不同的儲存節點上,那麼就能容忍m個節點故障。

圖1
圖1中的D、C的長度均為一個字(word),例如1個位元組、1個bit。D為源資料,C為校驗資料。
那麼問題來了: 糾刪碼是如何計算校驗資料的呢?又是如何恢復源資料的呢?
糾刪碼有很多種,這裡介紹廣泛應用:
Reed-Solomon糾刪碼
以冗餘級別為5+3的糾刪碼為例說明。將n個源資料塊D1~Dn按列排成向量D,再構造一個(n+m)*n矩陣B (圖2),B稱為分佈矩陣。對矩陣B有一個要求:它的任意n個行向量都是相互獨立的,即這n個行向量組成的n*n矩陣可逆。矩陣B的前n行是單位矩陣I,後m行的構造方法放在最後一段介紹,這裡先掠過。

圖2
執行矩陣向量乘B*D,得到m個校驗塊C1~ Cm(圖3)。
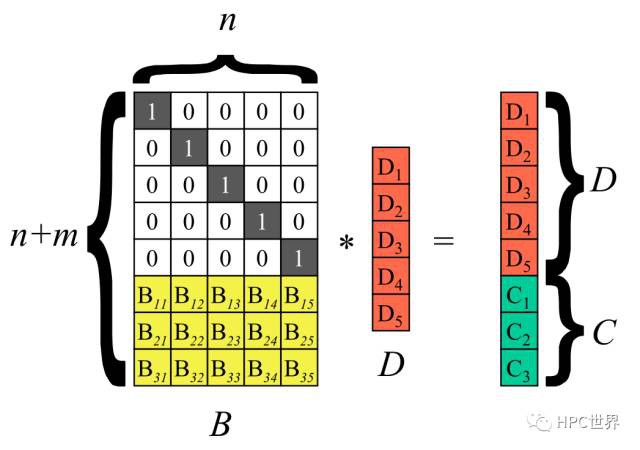
圖3
資料恢復演演算法
假設m個硬碟發生了故障,即圖4中的資料塊D1、D4、C2丟失,需要從剩下的n個資料塊中恢復出來源資料D1~Dn。

圖4
從矩陣B中將剩餘資料塊對應的行向量挑出來,組成新矩陣B’,B’乘以向量D的結果恰好是未故障的資料塊(圖5)。

圖5
因為B的任意n行組成的矩陣都可逆,所以矩陣B’存在逆矩陣,記為B’-1,顯然有B’-1*B’=I。

將圖5中等式的左右兩邊同時左乘矩陣B’-1,就得到了n個源資料塊D1~Dn,完成資料恢復。



Vandermonde矩陣
分佈矩陣B的構造方式有很多種,這裡介紹一種常用方法。
由線性代數知道,對互不相等的實數a1,a2,…,ak(k≥n),矩陣V的任意n行組成的矩陣都可逆。

從Vandermonde矩陣V中取出m行,用做分佈矩陣B的下部m行,恰好滿足對B的要求:任意n行都相互獨立。例如冗餘級別為6+3糾刪碼的分佈矩陣B可以採用如下形式。

簡單總結: 糾刪碼和大家熟悉的RAID技術看起來是有些類似,一個條帶(Stripe)是由多個資料塊(Strip)構成,分為資料塊和校驗塊。但與RAID5、RAID6不同的是糾刪碼從功能上來看最大的區分特點是校驗和資料的比例按N+M可調整,並且校驗塊數量不再受限於2個(RAID最多2個,比如RAID6),糾刪碼的M可以是3、4甚至更多。
相對傳統RAID技術,系統的容錯能力得到大幅度的提高,即可以允許系統內同時損壞的硬碟數量(或者儲存節點數)大幅度增加;實現了多對多的快速的資料重構,傳統RAID方式需要十幾個小時的重構時間,而這種方式磁碟重構時間可以縮短至分鐘級的速度。
原文連結: 糾刪碼的原理竟如此簡單
推薦閱讀:
溫馨提示:
請搜尋“ICT_Architect”或“掃一掃”二維碼關註公眾號,點選原文連結獲取電子書詳情。

求知若渴, 虛心若愚

 知識星球
知識星球