
來源:經管之家
ID:jgjgedu
極大似然估計(Maximum likelihood estimation, 簡稱MLE)是很常用的引數估計方法,極大似然原理的直觀想法是,一個隨機試驗如有若干個可能的結果A,B,C,… ,若在一次試驗中,結果A出現了,那麼可以認為實驗條件對A的出現有利,也即出現的機率P(A)較大。也就是說,如果已知某個隨機樣本滿足某種機率分佈,但是其中具體的引數不清楚,引數估計就是透過若干次試驗,觀察其結果,利用結果推出引數的大概值。極大似然估計是建立在這樣的思想上:已知某個引數能使這個樣本出現的機率最大,我們當然不會再去選擇其他小機率的樣本,所以乾脆就把這個引數作為估計的真實值(請參見“百度百科”)。
本文以一個簡單的離散型分佈的例子,模擬投擲硬幣估計頭像(head)向上的機率。投擲硬幣落到地面後,不是head向上就是tail朝上,這是一個典型的伯努利實驗,形成一個伯努利分佈,有著如下的離散機率分佈函式:
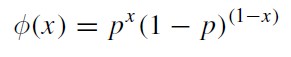
其中,x等於1或者0,即結果,這裡用1表示head、0表示tail。
對於n次獨立的投擲,很容易寫出其似然函式:

現在想用極大似然估計的方法把p估計出來。就是使得上面這個似然函式取極大值的情況下的p的取值,就是要估計的引數。
首先用Python把投擲硬幣模擬出來:
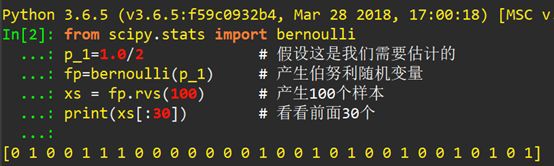
透過此模擬,使用sympy庫把似然函式寫出來:

從上面的結論可以看出,作100次伯努利實驗,出現positive、1及head的數目是53個,相應的0也就是tail的數目是47個,比較接近我們設的初始值0.5即1.0/2(註意:現在我們假設p是未知的,要去估計它,看它經過Python的極大似然估計是不是0.5!)。
下麵,我們使用Python求解這個似然函式取極大值時的p值:

結果沒有什麼懸念,53/100的值很接近0.5!
取對數後,上面Python的演演算法最後實際上是求解下式為0的p值:
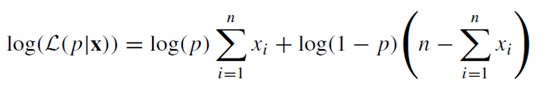
上式留給網友自行推導,很多資料都可找到該式。這個式子,是著名的Logistic回歸引數估計的極大似然估計演演算法的基礎。
進一步,為了更加直觀的理解投擲硬幣的伯努利實驗,我們給出以均值(均值為100*0.5=50)為中心對稱的加總離散機率(機率質量函式(probability mass function),Python裡面使用pmf函式計算):

對於上面的Python程式碼,可以透過下圖更好地去理解:
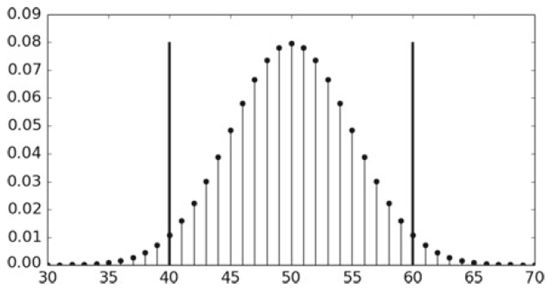
把這20個離散的機率全部顯示出來,也可以看到在0.08左右取到它們的最大值:

本文針對簡單的離散機率質量函式的分佈使用Python進行了極大似然估計,同時該方法可以應用於連續分佈的情形,只要透過其機率密度函式得出其似然函式即可。希望網友把本文的程式碼實踐一遍,也可以和R語言、SAS等軟體得到的結論相比較,從而得到更好的極大似然估計的實現方法。
《Linux雲端計算及運維架構師高薪實戰班》2018年08月27日即將開課中,120天衝擊Linux運維年薪30萬,改變速約~~~~
*宣告:推送內容及圖片來源於網路,部分內容會有所改動,版權歸原作者所有,如來源資訊有誤或侵犯權益,請聯絡我們刪除或授權事宜。
– END –


更多Linux好文請點選【閱讀原文】哦
↓↓↓
 知識星球
知識星球