讓我去健身的不是漂亮小姐姐，居然是貝葉斯統計-知識星球

導讀：今天將為大家介紹利用貝葉斯統計的一個實踐案例。通專案實踐達到學以致用的目的，相信大家對貝葉斯統計的理解和掌握都可以更深入，提煉出更精煉的內容。

譯者：劉暢

來源：人工智慧頭條（ID：AI_Thinker）

00 前言

我來自越南，在新加坡上高中，目前在美國上大學。我經常聽到身邊的人取笑我看起來很“嬌小”，我應該怎樣做運動，去健身房增重，然後才能有“更好的體格”… …然而我對這些評論卻是懷疑的，對於身高1.69米（5’6）和體重58kg（127lb）的人來說，我有接近完美的 BMI 指數（20.3）。

後來我明白他們沒有在談論 BMI，他們強調的是體型。

想想看，他們的出發點是好的：資料顯示越南男性的平均身高與體重是1米62和58kg，鑒於我身高高出了平均值，但體重與越南男性平均體重卻相同，我可能會“看起來”更瘦一些。“看起來”圈起來劃重點。如果體重相同，但是身高更高，那看起來更苗條更修長，這是一件邏輯很簡單的事。而我在考慮這是一個值得進一步探究的科學問題。

那麼問題來了，在身高1米69的越南男性中，我的體型有多瘦小？

我們需要一種方法論的方法來研究這個主題，一個好方法是盡可能多地找到越南男子身高和體重的資料，看看我的資料處於哪個位置。

01 越南人口概況

在網上搜索後，我找到了一份包含超過10,000名越南人的人口統計資訊調查研究資料。我將樣本量範圍縮小到18-29歲年齡段的男性。這使我有383名年齡在18-29歲左右的越南男性的樣本，對於接下來的分析來說已經是足夠的了。

首先畫出人口重量直方圖，看看我在越南男性中哪個位置。

▲紅線顯示樣本的中位數，橙色線顯示均值

這個圖表明，我略低於這383名越南青年體重的平均數和中位數。是好訊息嗎？然而，問題的重點並不在於我的體重與樣本相比如何。假設越南男性人口的健康狀況良好，並且整個越南人口可以由這383個人代表，但考慮到1米68的身高因素，我們可以推斷出我的體重與整個越南人口相比是什麼情況。為此，我們需要深入研究回歸分析。

第一步繪製關於身高和體重的二維散點圖。

好吧，我的資料看起來處在很平均的位置上。實際上，如果我們只檢視那些身高168cm的人的資料（想象一條在168cm處的垂直線，並穿過紅點），那麼我的體重比這些人稍輕一些。

另一個觀察到的重要結果是，散點圖的離散程度表明瞭越南男性的身高和體重之間存在著較強的線性關係。我們將進行定量分析以深入瞭解這種關係。

我們需要做的是快速新增“標準的最小二乘”線。稍後我會更多地介紹這條線，但現在先展示它。

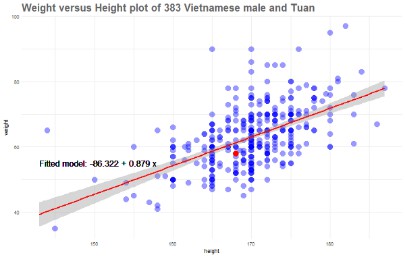
我們的最小二乘線是y = -86.32 + 0.889x，會發現在我這個年齡的越南男性的通常情況是，高1釐米體重就會增加0.88千克。

但是，這並不能回答我們的問題。在身高為1米68時，58公斤的體重會被認為是太重，太輕或只是平均？為了更加定量地解釋這個問題，如果我們有一個身高為1米68的人的分佈，我的體重下降到25,50或75個百分點的機率是多少？要做到這一點，需要我們深入挖掘並理解回歸背後的理論。

02 線性回歸的理論

線上性回歸模型中，Y變數的預期值（在我們的例子中，人的體重）是X（高度）的線性函式。我們稱之為線性關係，其中 β0 和 β1 分別是截距和斜率; 也就是說，我們假設E（Y | X = x）= β0 + β1 * X。但是我們不知道 β0 和 β1 的值，因此它就是未知引數。

在最標準的線性回歸模型中，我們進一步假設給定 X = x下Y的條件分佈是正態分佈的。這意味著簡單的線性回歸模型：

可以寫成下麵的形式，註意，在許多模型中，我們可以用精度引數 τ 替換方差引數 σ，其中 τ = 1 / σ。

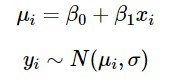
總結：因變數 Y 服從滿足平均值 μi 和精度引數 τ 的正態分佈。μi 與由 β0 和 β1 引數化的 X 是線性關係。

最後，我們還假設未知方差不依賴於 x ；這個假設被稱為同方差。

上述內容可能有點多，可以在下麵這張圖中看到剛討論過的內容。

在實際的資料分析問題中，我們只給出黑點（資料）。我們的標的是使用這些資料，對我們不知道的事情做出推斷，包括 β0，β1（陰影，藍色虛線）和 σ（紅色正常密度的寬度）。註意每個點周圍的正態分佈看起來完全相同。這是同方差性的性質。

03 引數估計

現在，你可以透過幾種方法來估計 β0 和 β1。如果你使用最小二乘法來估計此類模型，則不必擔心機率公式，因為你搜索 β0 和 β1 的最優值的方式是使擬合值與預測值的平方誤差最小化。另一種，可以使用最大似然估計來估計這種模型，你可以透過最大化似然函式來尋找引數的最優值。

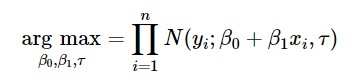
註意：一個有趣的結果是（這裡沒有數學證明），如果我們進一步假設誤差也屬於正態分佈，則最小二乘估計量也是最大似然估計量。

04 使用貝葉斯觀點的線性回歸

貝葉斯方法不是單獨最大化似然函式，而是假設了引數的先驗分佈並使用貝葉斯定理：

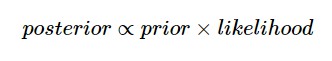
似然函式與上面的相同，但是不同之處在於對待估計引數β0，β1，τ假設了一些先驗分佈並且將它們包括到了等式中：

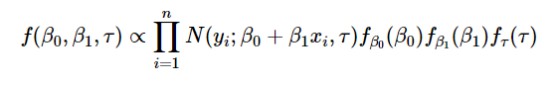
“什麼是先驗，為什麼我們的方程看起來複雜了10倍？”

相信我，這個先驗資訊雖然看起來感覺有點奇怪，但它非常直觀。事實是，有一個非常強烈的哲學推理，為什麼我們可以使用一些看似任意的分佈來確定一個未知引數（在我們的例子中是β0，β1，τ）。這些先驗分佈是為了在看到資料之前捕捉我們對資料分佈特點的看法。在觀察一些資料之後，我們應用貝葉斯規則來獲得這些未知引數的後驗分佈，它考慮了先驗資訊和資料。從這個後驗分佈我們可以計算資料的預測分佈。

這些先驗分佈是為了表達我們在看到資料之前，對資料分佈特點的一種假設。

最終的估計值將取決於（1）你的資料和（2）先驗資訊，但資料中包含的資訊越多，先驗資訊的作用就越小。

“所以我可以選擇先驗分佈嗎？”

這是一個很好的問題，因為有無限的選擇。（理論上）只有一個正確的先驗，即表示你的先驗假設。然而，在實踐中，先驗分佈的選擇可能相當主觀，有時甚至是任意的。我們可以選擇標準偏差較大的正態先驗（小精度）。例如，我們可以假設 β0 和 β1 是來自均值為 0 和標準差為 10,000 的正態分佈。這被稱為無資訊先驗，因為基本上這種分佈將是相當平坦的（即，它為特定範圍內的任何值分配幾乎相等的機率）。

接下來，如果這種先驗分佈是我們的選擇，我們不必擔心哪個分佈可能會更好，因為它的形狀幾乎都是平坦的，並且後驗分佈並不關心先驗分佈的分佈情況特點。

同樣，對於精度 τ，我們知道這些必須是非負的，所以選擇一個限製為非負值的分佈是有意義的。例如，我們可以使用低形狀和尺度引數的 Gamma 分佈。

另一個有用的非資訊選擇是均勻分佈。如果你選擇σ或τ的均勻分佈，你可能會得到John K. Kruschke所說的模型。

05 用R和JAGS進行模擬

迄今為止這個理論非常好。求解方程在數學上具有挑戰性。在絕大多數情況下，後驗分佈不會直接可用（正態分佈和 Gamma 分佈是多麼的複雜，你必須將其中的一系列資料乘在一起）。

馬爾可夫鏈蒙特卡羅方法通常用於估計模型的引數。JAGS工具包幫助我們做到了這一點。

JAGS工具是基於馬爾可夫鏈蒙特卡羅（MCMC）的模擬過程，能產生引數空間 θ =（β0;β1;τ）的許多迭代結果。在該引數空間中為每個引數生成的樣本分佈將接近該引數的總體分佈。

為什麼會這樣？解釋非常複雜。簡單的解釋就是：MCMC透過構建具有標的後驗分佈的馬爾可夫鏈，從而在後驗分佈中生成樣本。

講真它並不好玩。與通常解析方程（2）的方式不同，我們可以做一些聰明的抽樣，從數學角度證明我們樣本的分佈是 β0，β1，τ 的實際分佈。

06 如何使用這個JAGS工具呢

我們在R中透過如下步驟執行JAGS。

第一步，我們用文字格式編寫我們的模型：

然後，我們使用JAGs進行模擬。在這裡，我設定 JAGs 模擬引數空間θ 10000次的值。在這樣的取樣之後，我們可以得到如下所示θ=（β0;β1;τ）的取樣資料。

現在我們對引數空間θ進行10,000次迭代，記住透過公式：

這意味著，如果我們用 x = 168 cm 代替每次迭代，我們將找到 10,000 個體重值，並且因此給出高度為 168 cm 的體重分佈。

我們現在是在給定身高條件下，計算我體重的百分位。我們能做的就是根據我的身高找到我體重百分位數的分佈。

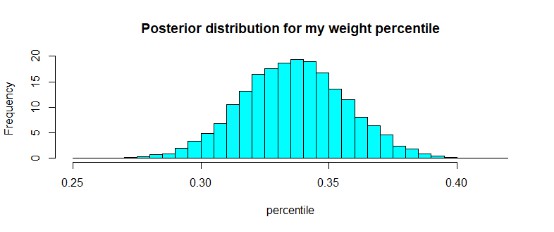
現在，這個圖告訴我們的是，我的體重（給定168釐米的身高）最有可能位於越南人口模擬資料的0.3％左右。例如，我們可以找到我的體重在前40個百分點或更少的百分位數。

所以絕大多數證據表明身高168釐米，體重58公斤會使我處於越南人口分佈中百分位數較低的位置。也許是時候去健身房並增加一些體重了。畢竟，如果你不能相信貝葉斯統計的結果，你還能相信什麼呢？

原作者：Tuan Doan Nguyen

原文連結：

https://towardsdatascience.com/how-bayesian-statistics-convinced-me-to-hit-the-gym-fa737b0a7ac

R 原始碼地址：

https://github.com/tuangauss/Various-projects/blob/master/R/bayesian_gym.R

讓我去健身的不是漂亮小姐姐，居然是貝葉斯統計

相關推薦

熱門標籤

熱門文章

分享創造快樂