(點選上方藍字,快速關註我們)
來自:眾成翻譯,譯者 sea_ljf,《奇舞週刊》排版編輯
連結:https://www.zcfy.cc/article/data-structures-for-beginners-arrays-hashmaps-and-lists

當開發程式時,我們(通常)需要在記憶體中儲存資料。根據運算元據方式的不同,可能會選擇不同的資料結構。有很多常用的資料結構,如:Array、Map、Set、List、Tree、Graph 等等。(然而)為程式選取合適的資料結構可能並不容易。因此,希望這篇文章能幫助你瞭解(不同資料結構的)表現,以求在工作中合理地使用它們。
本文主要聚焦於線性的資料結構,如:Array、Set、List、Sets、Stacks、Queues 等等。
本篇是以下教程的一部分(譯者註:如果大家覺得還不錯,我會翻譯整個系列的文章):
初學者應該瞭解的資料結構與演演算法(DSA)
-
演演算法的時間複雜性與大 O 符號
-
每個程式員應該知道的八種時間複雜度
-
初學者應該瞭解的資料結構:Array、HashMap 與 List ? 即本文
-
初學者應該瞭解的資料結構: Graph
-
初學者應該瞭解的資料結構:Tree (敬請期待)
-
附錄 I:遞迴演演算法分析
(操作)資料結構的時間複雜度
下表是本文所討論內容的概括。
* = 執行時分攤
註意: 二叉搜尋樹 與其他樹結構、圖結構,將在另一篇文章中討論。
原始資料型別
原始資料型別是構成資料結構最基礎的元素。下麵列舉出一些原始原始資料型別:
-
整數,如:1, 2, 3, …
-
字元,如:a, b, “1”, “*”
-
布林值, true 與 false.
-
浮點數 ,如:3.14159, 1483e-2.
Array
陣列可由零個或多個元素組成。由於陣列易於使用且檢索效能優越,它是最常用的資料結構之一。
你可以將陣列想象成一個抽屜,可以將資料存到匣子中。
陣列就像是將東西存到匣子中的抽屜

當你想查詢某個元素時,你可以直接開啟對應編號的匣子(時間複雜度為 O(1))。然而,如果你忘記了匣子裡存著什麼,就必須逐個開啟所有的匣子(時間複雜度為 O(n)),直到找到所需的東西。陣列也是如此。
根據程式語言的不同,陣列存在一些差異。對於 JavaScript 和 Ruby 等動態語言而言,陣列可以包含不同的資料型別:數字,字串,物件甚至函式。而在 Java 、 C 、C ++ 之類的強型別語言中,你必須在使用陣列之前,定好它的長度與資料型別。JavaScript 會在需要時自動增加陣列的長度。
Array 的內建方法
根據程式設計式言的不同,陣列(方法)的實現稍有不同。
比如在 JavaScript 中,我們可以使用 unshift 與 push 新增元素到陣列的頭或尾,同時也可以使用 shift 與 pop 刪除陣列的首個或最後一個元素。讓我們來定義一些本文用到的陣列常用方法。
常用的 JS 陣列內建函式
向陣列插入元素
將元素插入到陣列有很多方式。你可以將新資料新增到陣列末尾,也可以新增到陣列開頭。
先看看如何新增到末尾:
function insertToTail(array, element) {
array.push(element);
return array;
}
const array = [1, 2, 3];
console.log(insertToTail(array, 4)); // => [ 1, 2, 3, 4 ]
根據規範,push 操作只是將一個新元素新增到陣列的末尾。因此,
現在看看如新增到開頭:
function insertToHead(array, element) {
array.unshift(element);
return array;
}
const array = [1, 2, 3];
console.log(insertToHead(array, 0));// => [ 0, 1, 2, 3, ]
你覺得新增元素到陣列開頭的函式,時間複雜度是什麼呢?看起來和上面(push)差不多,除了呼叫的方法是 unshift 而不是 push。但這有個問題,unshift 是透過將陣列的每一項移到下一項,騰出首項的空間來容納新新增的元素。所以它是遍歷了一次陣列的。
訪問陣列中的元素
如果你知道待查詢元素在陣列中的索引,那你可以透過以下方法直接訪問該元素:
function access(array, index) {
return array[index];
}
const array = [1, 'word', 3.14, { a: 1 }];
access(array, 0);// => 1
access(array, 3);// => {a: 1}
正如上面你所看到的的程式碼一樣,訪問陣列中的元素耗時是恆定的:
註意:透過索引修改陣列的值所花費的時間也是恆定的。
在陣列中查詢元素
如果你想查詢某個元素但不知道對應的索引時,那隻能透過遍歷陣列的每個元素,直到找到為止。
function search(array, element) {
for (let index = 0;
index < array.length;
index++) {
if (element === array[index]) {
return index;
}
}
}
const array = [1, 'word', 3.14, { a: 1 }];
console.log(search(array, 'word'));// => 1
console.log(search(array, 3.14));// => 2
鑒於使用了 for 迴圈,那麼:
在陣列中刪除元素
你覺得從陣列中刪除元素的時間複雜度是什麼呢?
先一起思考下這兩種情況:
-
從陣列的末尾刪除元素所需時間是恆定的,也就是 O(1)。
-
然而,無論是從陣列的開頭或是中間位置刪除元素,你都需要調整(刪除元素後面的)元素位置。因此複雜度為 O(n)。
說多無謂,看程式碼好了:
function remove(array, element) {
const index = search(array, element);
array.splice(index, 1);
return array;
}
const array1 = [0, 1, 2, 3];
console.log(remove(array1, 1));// => [ 0, 2, 3 ]
我們使用了上面定義的 search 函式來查詢元素的的索引,複雜度為 O(n)。然後使用JS 內建的 splice 方法,它的複雜度也是 O(n)。那(刪除函式)總的時間複雜度不是 O(2n) 嗎?記住,(對於時間複雜度而言,)我們並不關心常量。
對於上面列舉的兩種情況,考慮最壞的情況:
陣列方法的時間複雜度
在下表中,小結了陣列(方法)的時間複雜度:
陣列方法的時間複雜度
HashMaps
HashMap有很多名字,如 HashTable、HashMap、Map、Dictionary、Associative Array 等。概念上它們都是一致的,實現上稍有不同。
回想一下關於抽屜的比喻,現在匣子有了標簽,不再是按數字順序了。
HashMap 也和抽屜一樣儲存東西,透過不同標識來區分不同匣子。

此例中,如果你要找一個玩具,你不需要依次開啟第一個、第二個和第三個匣子來檢視玩具是否在內。直接代開被標識為“玩具”的匣子即可。這是一個巨大的進步,查詢元素的時間複雜度從 O(n) 降為 O(1) 了。
數字是陣列的索引,而標識則作為 HashMap 儲存資料的鍵。HashMap 內部透過 雜湊函式 將鍵(也就是標識)轉化為索引。
至少有兩種方式可以實現 hashmap:
-
陣列:透過雜湊函式將鍵對映為陣列的索引。(查詢)最差情況: O(n),平均: O(1)。
-
二叉搜尋樹: 使用自平衡二叉搜尋樹查詢值(另外的文章會詳細介紹)。 (查詢)最差情況: O(log n),平均:O(log n)。
我們會介紹樹與二叉搜尋樹,現在先不用擔心太多。實現 Map 最常用的方式是使用 陣列與雜湊轉換函式。讓我們(透過陣列)來實現它吧
透過陣列實現 HashMap

正如上圖所示,每個鍵都被轉換為一個 hash code。由於陣列的大小是有限的(如此例中是10),(如發生衝突,)我們必須使用模函式找到對應的桶(譯者註:桶指的是陣列的項),再迴圈遍歷該桶(來尋找待查詢的值)。每個桶內,我們儲存的是一組組的鍵值對,如果桶記憶體儲了多個鍵值對,將採用集合來儲存它們。
我們將講述 HashMap 的組成,讓我們先從雜湊函式開始吧。
雜湊函式
實現 HashMap 的第一步是寫出一個雜湊函式。這個函式會將鍵對映為對應(索引的)值。
藉助理想的雜湊函式,可以實現訪問與查詢在恆定時間內完成。然而,完美的雜湊函式在實踐中是難以實現的。你很可能會碰到兩個不同的鍵被對映為同一索引的情況,也就是 衝突。
當使用類似陣列之類的資料結構作為 HashMap 的實現時,衝突是難以避免的。因此,解決衝突的其中一種方式是在同一個桶中儲存多個值。當我們試圖訪問某個鍵對應的值時,如果在對應的桶中發現多組鍵值對,則需要遍歷它們(以尋找該鍵對應的值),時間複雜度為 O(n)。然而,在大多數(HashMap)的實現中, HashMap 會動態調整陣列的長度以免衝突發生過多。因此我們可以說分攤後的查詢時間為 O(1)。本文中我們將透過一個例子,講述分攤的含義。
HashMap 的簡單實現
一個簡單(但糟糕)的雜湊函式可以是這樣的:
class NaiveHashMap {
constructor(initialCapacity = 2) {
this.buckets = new Array(initialCapacity);
}
set(key, value) {
const index = this.getIndex(key);
this.buckets[index] = value;
}
get(key) {
const index = this.getIndex(key);
return this.buckets[index];
}
hash(key) {
return key.toString().length;
}
getIndex(key) {
const indexHash = this.hash(key);
const index = indexHash % this.buckets.length;
return index;
}
}
完整程式碼
我們直接使用桶而不是抽屜與匣子,相信你能明白喻義的意思 🙂
HashMap 的初始容量(譯者註:容量指的是用於儲存資料的陣列長度,即桶的數量)是2(兩個桶)。當我們往裡面儲存多個元素時,透過求餘 % 計算出該鍵應存入桶的編號(,並將資料存入該桶中)。
留意程式碼的第18行(即 return key.toString().length;)。之後我們會對此進行一點討論。現在先讓我們使用一下這個新的 HashMap 吧。
// Usage:
const assert = require('assert');
const hashMap = new NaiveHashMap();
hashMap.set('cat', 2);
hashMap.set('rat', 7);
hashMap.set('dog', 1);
hashMap.set('art', 8);
console.log(hashMap.buckets);
/*
bucket #0: <1 empty item>,
bucket #1: 8
*/
assert.equal(hashMap.get('art'), 8); // this one is ok
assert.equal(hashMap.get('cat'), 8); // got overwritten by art ?
assert.equal(hashMap.get('rat'), 8); // got overwritten by art ?
assert.equal(hashMap.get('dog'), 8); // got overwritten by art ?
這個 HashMap 允許我們透過 set 方法設定一組鍵值對,透過往 get 方法傳入一個鍵來獲取對應的值。其中的關鍵是雜湊函式,當我們存入多組鍵值時,看看這 HashMap 的表現。
你能說出這個簡單實現的 HashMap 存在的問題嗎?
1) Hash function 轉換出太多相同的索引。如:
hash('cat') // 3
hash('dog') // 3
這會產生非常多的衝突。
2) 完全不處理衝突的情況。cat 與 dog 會重寫彼此在 HashMap 中的值(它們均在桶 #1 中)。
3 陣列長度。 即使我們有一個更好的雜湊函式,由於陣列的長度是2,少於存入元素的數量,還是會產生很多衝突。我們希望 HashMap 的初始容量大於我們存入資料的數量。
改進雜湊函式
為此,我們需要:
-
一個合適的雜湊函式,盡可能地減少衝突。
-
一個長度足夠大的陣列用於儲存資料。
讓我們重新設計雜湊函式,不再採用字串的長度為 hash code,取而代之是使用字串中每個字元的ascii 碼的總和為 hash code。
hash(key) {
let hashValue = 0;
const stringKey = key.toString();
for (let index = 0; index < stringKey.length; index++) {
const charCode = stringKey.charCodeAt(index);
hashValue += charCode;
}
return hashValue;
}
再試一次:
hash('cat') // 312 (c=99 + a=97 + t=116)
hash('dog') // 314 (d=100 + o=111 + g=103)
這函式比之前的要好!這是因為相同長度的單詞由不一樣的字母組成,因而 ascii 碼的總和不一樣。
然而,仍然有問題!單詞 rat 與 art 轉換後都是327,產生衝突了! ?
可以透過根據字元位置左移它的 ascii 碼來解決:
hash(key) {
let hashValue = 0;
const stringKey = `${key}`;
for (let index = 0; index < stringKey.length; index++) {
const charCode = stringKey.charCodeAt(index);
hashValue += charCode << (index * 8);
}
return hashValue;
}
現在繼續試驗,下麵列舉出了十六進位制的數字,這樣可以方便我們觀察位移。
// r = 114 or 0x72; a = 97 or 0x61; t = 116 or 0x74
hash('rat'); // 7,627,122 (r: 114 * 1 + a: 97 * 256 + t: 116 * 65,536) or in hex: 0x726174 (r: 0x72 + a: 0x6100 + t: 0x740000)
hash('art'); // 7,631,457 or 0x617274
然而,以下兩種型別有何不同呢?
hash(1); // 49
hash('1'); // 49
hash('1,2,3'); // 741485668
hash([1,2,3]); // 741485668
hash('undefined') // 3402815551
hash(undefined) // 3402815551
天啊,仍然有問題!!不同的資料型別不應該傳回相同的 hash code!
該如何解決呢?
其中一種方式是在雜湊函式中,將資料的型別作為轉換 hash code 的一部分。
hash(key) {
let hashValue = 0;
const stringTypeKey = `${key}${typeof key}`;
for (let index = 0; index < stringTypeKey.length; index++) {
const charCode = stringTypeKey.charCodeAt(index);
hashValue += charCode << (index * 8);
}
return hashValue;
}
讓我們讓我們再試一次:
console.log(hash(1)); // 1843909523
console.log(hash('1')); // 1927012762
console.log(hash('1,2,3')); // 2668498381
console.log(hash([1,2,3])); // 2533949129
console.log(hash('undefined')); // 5329828264
console.log(hash(undefined)); // 6940203017
Yay!!! ? 我們終於有了更好的雜湊函式!
同時,我們可以改變 HashMap 的原始容量以減少衝突,讓我們在下一節中最佳化 HashMap。
更完善的 HashMap 實現
透過最佳化好的雜湊函式,HashMap 可以表現得更好。
儘管衝突仍可能發生,但透過一些方式可以很好地處理它們。
對於我們的 HashMap,希望有以下改進:
-
雜湊函式, 檢查型別與計算各字元(ascii 碼的總和)以減少衝突的發生。
-
處理衝突,透過將值新增到集合中來解決這問題,同時需要一個計數器追蹤衝突的數量。
更完善 HashMap 實現完整程式碼
class DecentHashMap {
constructor(initialCapacity = 2) {
this.buckets = new Array(initialCapacity);
this.collisions = 0;
}
set(key, value) {
const bucketIndex = this.getIndex(key);
if(this.buckets[bucketIndex]) {
this.buckets[bucketIndex].push({key, value});
if(this.buckets[bucketIndex].length > 1) { this.collisions++; }
} else {
this.buckets[bucketIndex] = [{key, value}];
}
return this;
}
get(key) {
const bucketIndex = this.getIndex(key);
for (let arrayIndex = 0; arrayIndex < this.buckets[bucketIndex].length; arrayIndex++) {
const entry = this.buckets[bucketIndex][arrayIndex];
if(entry.key === key) {
return entry.value
}
}
}
hash(key) {
let hashValue = 0;
const stringTypeKey = `${key}${typeof key}`;
for (let index = 0; index < stringTypeKey.length; index++) {
const charCode = stringTypeKey.charCodeAt(index);
hashValue += charCode << (index * 8);
}
return hashValue;
}
getIndex(key) {
const indexHash = this.hash(key);
const index = indexHash % this.buckets.length;
return index;
}
}
看看這個 HashMap 表現如何:
// Usage:
const assert = require('assert');
const hashMap = new DecentHashMap();
hashMap.set('cat', 2);
hashMap.set('rat', 7);
hashMap.set('dog', 1);
hashMap.set('art', 8);
console.log('collisions: ', hashMap.collisions); // 2
console.log(hashMap.buckets);
/*
bucket #0: [ { key: 'cat', value: 2 }, { key: 'art', value: 8 } ]
bucket #1: [ { key: 'rat', value: 7 }, { key: 'dog', value: 1 } ]
*/
assert.equal(hashMap.get('art'), 8); // this one is ok
assert.equal(hashMap.get('cat'), 2); // Good. Didn't got overwritten by art
assert.equal(hashMap.get('rat'), 7); // Good. Didn't got overwritten by art
assert.equal(hashMap.get('dog'), 1); // Good. Didn't got overwritten by art
完善後的 HashMap 很好地完成了工作,但仍然有一些問題。使用改良後的雜湊函式不容易產生重覆的值,這非常好。然而,在桶#0與桶#1中都有兩個值。這是為什麼呢??
由於 HashMap 的容量是2,儘管算出來的 hash code 是不一樣的,當求餘後算出所需放進桶的編號時,結果不是桶#0就是桶#1。
hash('cat') => 3789411390; bucketIndex => 3789411390 % 2 = 0
hash('art') => 3789415740; bucketIndex => 3789415740 % 2 = 0
hash('dog') => 3788563007; bucketIndex => 3788563007 % 2 = 1
hash('rat') => 3789411405; bucketIndex => 3789411405 % 2 = 1
很自然地想到,可以透過增加 HashMap 的原始容量來解決這個問題,但原始容量應該是多少呢?先來看看容量是如何影響 HashMap 的表現的。
如果初始容量是1,那麼所有的鍵值對都會被存入同一個桶,即桶#0。查詢操作並不比純粹用陣列儲存資料的時間複雜度簡單,它們都是 O(n)。
而假設將初始容量定為10:
const hashMapSize10 = new DecentHashMap(10);
hashMapSize10.set('cat', 2);
hashMapSize10.set('rat', 7);
hashMapSize10.set('dog', 1);
hashMapSize10.set('art', 8);
console.log('collisions: ', hashMapSize10.collisions); // 1
console.log('hashMapSize10 ', hashMapSize10.buckets);
/*
bucket#0: [ { key: 'cat', value: 2 }, { key: 'art', value: 8 } ],
<4 empty items>,
bucket#5: [ { key: 'rat', value: 7 } ],
<1 empty item>,
bucket#7: [ { key: 'dog', value: 1 } ],
<2 empty items>
*/
換個角度看:

正如你所看到的,透過增加 HashMap 的容量,能有效減少衝突次數。
那換個更大的試試怎樣,比如 ?:
const hashMapSize100 = new DecentHashMap(100);
hashMapSize100.set('cat', 2);
hashMapSize100.set('rat', 7);
hashMapSize100.set('dog', 1);
hashMapSize100.set('art', 8);
console.log('collisions: ', hashMapSize100.collisions); // 0
console.log('hashMapSize100 ', hashMapSize100.buckets);
/*
<5 empty items>,
bucket#5: [ { key: 'rat', value: 7 } ],
<1 empty item>,
bucket#7: [ { key: 'dog', value: 1 } ],
<32 empty items>,
bucket#41: [ { key: 'art', value: 8 } ],
<49 empty items>,
bucket#90: [ { key: 'cat', value: 2 } ],
<9 empty items>
*/
Yay! ? 沒有衝突!
透過增加初始容量,可以很好的減少衝突,但會消耗更多的記憶體,而且很可能許多桶都沒被使用。
如果我們的 HashMap 能根據需要自動調整容量,這不是更好嗎?這就是所謂的rehash(重新計算雜湊值),我們將在下一節將實現它!
最佳化HashMap 的實現
如果 HashMap 的容量足夠大,那就不會產生任何衝突,因此查詢操作的時間複雜度為 O(1)。然而,我們怎麼知道容量多大才是足夠呢,100?1000?還是一百萬?
(從開始就)分配大量的記憶體(去建立陣列)是不合理的。因此,我們能做的是根據裝載因子動態地調整容量。這操作被稱為 rehash。
裝載因子是用於衡量一個 HashMap 滿的程度,可以透過儲存鍵值對的數量除以 HashMap 的容量得到它。
根據這思路,我們將實現最終版的 HashMap:
最佳的 HasnMap 實現
class HashMap {
constructor(initialCapacity = 16, loadFactor = 0.75) {
this.buckets = new Array(initialCapacity);
this.loadFactor = loadFactor;
this.size = 0;
this.collisions = 0;
this.keys = [];
}
hash(key) {
let hashValue = 0;
const stringTypeKey = `${key}${typeof key}`;
for (let index = 0; index < stringTypeKey.length; index++) {
const charCode = stringTypeKey.charCodeAt(index);
hashValue += charCode << (index * 8);
}
return hashValue;
}
_getBucketIndex(key) {
const hashValue = this.hash(key);
const bucketIndex = hashValue % this.buckets.length;
return bucketIndex;
}
set(key, value) {
const {bucketIndex, entryIndex} = this._getIndexes(key);
if(entryIndex === undefined) {
// initialize array and save key/value
const keyIndex = this.keys.push({content: key}) - 1; // keep track of the key index
this.buckets[bucketIndex] = this.buckets[bucketIndex] || [];
this.buckets[bucketIndex].push({key, value, keyIndex});
this.size++;
// Optional: keep count of collisions
if(this.buckets[bucketIndex].length > 1) { this.collisions++; }
} else {
// override existing value
this.buckets[bucketIndex][entryIndex].value = value;
}
// check if a rehash is due
if(this.loadFactor > 0 && this.getLoadFactor() > this.loadFactor) {
this.rehash(this.buckets.length * 2);
}
return this;
}
get(key) {
const {bucketIndex, entryIndex} = this._getIndexes(key);
if(entryIndex === undefined) {
return;
}
return this.buckets[bucketIndex][entryIndex].value;
}
has(key) {
return !!this.get(key);
}
_getIndexes(key) {
const bucketIndex = this._getBucketIndex(key);
const values = this.buckets[bucketIndex] || [];
for (let entryIndex = 0; entryIndex < values.length; entryIndex++) {
const entry = values[entryIndex];
if(entry.key === key) {
return {bucketIndex, entryIndex};
}
}
return {bucketIndex};
}
delete(key) {
const {bucketIndex, entryIndex, keyIndex} = this._getIndexes(key);
if(entryIndex === undefined) {
return false;
}
this.buckets[bucketIndex].splice(entryIndex, 1);
delete this.keys[keyIndex];
this.size--;
return true;
}
rehash(newCapacity) {
const newMap = new HashMap(newCapacity);
this.keys.forEach(key => {
if(key) {
newMap.set(key.content, this.get(key.content));
}
});
// update bucket
this.buckets = newMap.buckets;
this.collisions = newMap.collisions;
// Optional: both `keys` has the same content except that the new one doesn't have empty spaces from deletions
this.keys = newMap.keys;
}
getLoadFactor() {
return this.size / this.buckets.length;
}
}
完整程式碼(譯者註:其實 has 方法有問題,只是不影響閱讀。)
註意第99行至第114行(即 rehash 函式),那裡是 rehash 魔法發生的地方。我們創造了一個新的 HashMap,它擁有原來 HashMap兩倍的容量。
測試一下上面的新實現吧:
const assert = require('assert');
const hashMap = new HashMap();
assert.equal(hashMap.getLoadFactor(), 0);
hashMap.set('songs', 2);
hashMap.set('pets', 7);
hashMap.set('tests', 1);
hashMap.set('art', 8);
assert.equal(hashMap.getLoadFactor(), 4/16);
hashMap.set('Pineapple', 'Pen Pineapple Apple Pen');
hashMap.set('Despacito', 'Luis Fonsi');
hashMap.set('Bailando', 'Enrique Iglesias');
hashMap.set('Dura', 'Daddy Yankee');
hashMap.set('Lean On', 'Major Lazer');
hashMap.set('Hello', 'Adele');
hashMap.set('All About That Bass', 'Meghan Trainor');
hashMap.set('This Is What You Came For', 'Calvin Harris ');
assert.equal(hashMap.collisions, 2);
assert.equal(hashMap.getLoadFactor(), 0.75);
assert.equal(hashMap.buckets.length, 16);
hashMap.set('Wake Me Up', 'Avicii'); //
assert.equal(hashMap.collisions, 0);
assert.equal(hashMap.getLoadFactor(), 0.40625);
assert.equal(hashMap.buckets.length, 32);
註意,在 HashMap 儲存了12項之後,裝載因子將超過0.75,因而觸發 rehash,HashMap 容量加倍(從16到32)。同時,我們也能看到衝突從2降低為0。
這版本實現的 HashMap 能以很低的時間複雜度進行常見的操作,如:插入、查詢、刪除、編輯等。
小結一下,HashMap 的效能取決於:
-
雜湊函式能根據不同的鍵輸出不同的值。
-
HashMap 容量的大小。
我們終於處理好了各種問題 ?。有了不錯的雜湊函式,可以根據不同輸入傳回不同輸出。同時,我們也有 rehash 函式根據需要動態地調整 HashMap的容量。這實在太好了!
HashMap 中插入元素的時間複雜度
往一個 HashMap 插入元素需要兩樣東西:一個鍵與一個值。可以使用上文開發最佳化後的 HashMap 或內建的物件進行操作:
function insert(object, key, value) {
object[key] = value;
return object;
}
const hash = {};
console.log(insert(hash, 'word', 1)); // => { word: 1 }
在新版的 JavaScript 中,你可以使用 Map。
function insertMap(map, key, value) {
map.set(key, value);
return map;
}
const map = new Map();
console.log(insertMap(map, 'word', 1)); // Map { 'word' => 1 }
註意。我們將使用 Map 而不是普通的物件,這是由於 Map 的鍵可以是任何東西而物件的鍵只能是字串或者數字。此外,Map 可以保持插入的順序。
進一步說,Map.set 只是將元素插入到陣列(如上文 DecentHashMap.set 所示),類似於 Array.push,因此可以說:
rehash 能將衝突可能性降至最低。rehash 操作時間複雜度是 O(n) ,但不是每次插入操作都要執行,僅在需要時執行。
HashMap 中查詢或訪問元素的時間複雜度
這是 HashMap.get 方法,我們透過往裡面傳遞一個鍵來獲取對應的值。讓我們回顧一下 DecentHashMap.get 的實現:
get(key){
const hashIndex = this .getIndex(key);
const values = this .array [hashIndex];
for(let index = 0 ; index <values.length; index ++){
const entry = values [index];
if(entry.key === key){
傳回 entry.value
}
}
}
如果並未發生衝突,那麼 values 只會有一個值,訪問的時間複雜度是 O(1)。但我們也知道,衝突總是會發生的。如果 HashMap 的初始容量太小或雜湊函式設計糟糕,那麼大多數元素訪問的時間複雜度是 O(n)。
進階提示:另一個(將訪問操作的)時間複雜度從 O(n) 降至 O(log n) 的方法是使用 二叉搜尋樹 而不是陣列進行底層儲存。事實上,當儲存的元素超過8 個時, Java HashMap 的底層實現會從陣列轉為樹。
HashMap 中修改或刪除元素的時間複雜度
修改(HashMap.set)或刪除(HashMap.delete)鍵值對,分攤後的時間複雜度是 O(1)。如果衝突很多,可能面對的就是最壞情況,複雜度為 O(n)。然而伴隨著 rehash 操作,可以大大減少最壞情況的發生的機率。
HashMap 方法的時間複雜度
在下表中,小結了 HashMap(方法)的時間複雜度:
HashMap 方法的時間複雜度
Sets
集合跟陣列非常相像。它們的區別是集合中的元素是唯一的。
我們該如何實現一個集合呢(也就是沒有重覆項的陣列)?可以使用陣列實現,在插入新元素前先檢查該元素是否存在。但檢查是否存在的時間複雜度是 O(n)。能對此進行最佳化嗎?之前開發的 Map (插入操作)分攤後時間複雜度度才 O(1)!
Set 的實現
可以使用 JavaScript 內建的 Set。然而透過自己實現它,可以更直觀地瞭解它的時間複雜度。我們將使用上文最佳化後帶有 rehash 功能的 HashMap 來實現它。
const HashMap = require('../hash-maps/hash-map');
class MySet {
constructor() {
this.hashMap = new HashMap();
}
add(value) {
this.hashMap.set(value);
}
has(value) {
return this.hashMap.has(value);
}
get size() {
return this.hashMap.size;
}
delete(value) {
return this.hashMap.delete(value);
}
entries() {
return this.hashMap.keys.reduce((acc, key) => {
if(key !== undefined) {
acc.push(key.content);
}
return acc
}, []);
}
}
(譯者註:由於 HashMap 的 has 方法有問題,導致 Set 的 has 方法也有問題)
我們使用 HashMap.set 為集合不重覆地新增元素。我們將待儲存的值作為 HashMap的鍵,由於雜湊函式會將鍵對映為唯一的索引,因而起到排重的效果。
檢查一個元素是否已存在於集合中,可以使用 hashMap.has 方法,它的時間複雜度平均是 O(1)。集合中絕大多數的方法分攤後時間複雜度為 O(1),除了 entries 方法,它的事件複雜度是 O(n)。
註意:使用 JavaScript 內建的集合時,它的 Set.has 方法時間複雜度是 O(n)。這是由於它的使用了 List 作為內部實現,需要檢查每一個元素。你可以在這查閱相關的細節。
下麵有些例子,說明如何使用這個集合:
const assert = require('assert');
// const set = new Set(); // Using the built-in
const set = new MySet(); // Using our own implementation
set.add('one');
set.add('uno');
set.add('one'); // should NOT add this one twice
assert.equal(set.has('one'), true);
assert.equal(set.has('dos'), false);
assert.equal(set.size, 2);
// assert.deepEqual(Array.from(set), ['one', 'uno']);
assert.equal(set.delete('one'), true);
assert.equal(set.delete('one'), false);
assert.equal(set.has('one'), false);
assert.equal(set.size, 1);
這個例子中,MySet 與 JavaScript 中內建的 Set 均可作為容器。
Set 方法的時間複雜度
根據 HashMap 實現的的 Set,可以小結出的時間複雜度如下(與 HashMap 非常相似):
Set 方法的時間複雜度
Linked Lists
連結串列是一種一個節點連結到下一個節點的資料結構。

連結串列是(本文)第一種不用陣列(作為底層)實現的資料結構。我們使用節點來實現,節點儲存了一個元素,並指向下一個節點(若沒有下一個節點,則為空)。
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
當每個節點都指向它的下了一個節點時,我們就擁有了一條由若干節點組成鏈條,即單向連結串列。
Singly Linked Lists
對於單向連結串列而言,我們只需關心每個節點都有指向下一個節點的取用。
從首個節點或稱之為根節點開始構建(單向連結串列)。
class LinkedList {
constructor() {
this.root = null;
}
// ...
}
每個連結串列都有四個基礎操作:
-
addLast:將一個元素新增至連結串列尾部。
-
removeLast:刪除連結串列的最後一個元素。
-
addFirst:將一個元素新增到連結串列的首部。
-
removeFirst:刪除連結串列的首個元素。
向連結串列末尾新增與刪除一個元素
(對新增操作而言,)有兩種情況。1)如果連結串列根節點不存在,那麼將新節點設定為連結串列的根節點。2)若存在根節點,則必須不斷查詢下一個節點,直到連結串列的末尾,並將新節點新增到最後。
addLast(value) { // similar Array.push
const node = new Node(value);
if(this.root) {
let currentNode = this.root;
while(currentNode && currentNode.next) {
currentNode = currentNode.next;
}
currentNode.next = node;
} else {
this.root = node;
}
}
上述程式碼的時間複雜度是多少呢?如果是作為根節點新增進連結串列,時間複雜度是 O(1),然而尋找最後一個節點的時間複雜度是 O(n).。
刪除末尾的節點與上述程式碼相差無幾。
removeLast() {
let current = this.root;
let target;
if(current && current.next) {
while(current && current.next && current.next.next) {
current = current.next;
}
target = current.next;
current.next = null;
} else {
this.root = null;
target = current;
}
if(target) {
return target.value;
}
}
時間複雜度也是 O(n)。這是由於我們必須依次往下,直到找到倒數第二個節點,並將它 next 的取用指向 null。
向連結串列開頭新增與刪除一個元素
往連結串列開頭新增一個元素(的程式碼)如下所示:
addFirst(value) {
const node = new Node(value);
node.next = this.first;
this.first = node;
}
向連結串列的開頭進行增刪操作,所耗費的時間是恆定的,因為我們持有根元素的取用:
removeFirst(value) {
const target = this.first;
this.first = target ? target.next : null;
return target.value;
}
(譯者註:作者原文 removeFirst 的程式碼放錯了,上述程式碼是譯者實現的)
如你所見,對連結串列的開頭進行增刪操作,時間複雜度永遠是 O(1)。
從連結串列的任意位置刪除元素
刪除連結串列首尾的元素,可以使用 removeFirst 或 removeLast。然而,如若移除的節點在連結串列的中間,則需要將待刪除節點的前一個節點指向待刪除節點的下一個節點,從而從連結串列中刪除該節點:
remove(index = 0) {
if(index === 0) {
return this.removeFirst();
}
let current;
let target = this.first;
for (let i = 0; target; i++, current = target, target = target.next) {
if(i === index) {
if(!target.next) { // if it doesn't have next it means that it is the last
return this.removeLast();
}
current.next = target.next;
this.size--;
return target.value;
}
}
}
(譯者註:原文實現有點問題,譯者稍作了點修改。removeLast 的呼叫其實浪費了效能,但可讀性上增加了,因而此處未作修改。)
註意, index 是從0開始的:0是第一個節點,1是第二個,如此類推。
在連結串列中查詢元素
在連結串列中查詢一個元素與刪除元素的程式碼差不多:
contains(value) {
for (let current = this.first, index = 0; current; index++, current = current.next) {
if(current.value === value) {
return index;
}
}
}
這個方法查詢連結串列中第一個與給定值相等的節點(的索引)。
單向連結串列操作方法的時間複雜度
在下表中,小結了單向連結串列(方法)的時間複雜度:
註意,當我們增刪連結串列的最後一個元素時,該操作的時間複雜度是 O(n)…
我們將在下一節實現這功能!
Doubly Linked Lists
當我們有一串節點,每一個都有指向下一個節點的取用,也就是擁有了一個單向連結串列。而當一串節點,每一個既有指向下一個節點的取用,也有指向上一個節點的取用時,這串節點就是雙向連結串列。

雙向連結串列的節點有兩個取用(分別指向前一個和後一個節點),因此需要保持追蹤首個與最後一個節點。
class Node {
constructor(value) {
this.value = value;
this.next = null;
this.previous = null;
}
}
class LinkedList {
constructor() {
this.first = null; // head/root element
this.last = null; // last element of the list
this.size = 0; // total number of elements in the list
}
// ...
}
(雙向連結串列的完整程式碼)
新增或刪除連結串列的首個元素
由於持有首個節點的取用,因而新增或刪除首個元素的操作是十分簡單的:
addFirst(value) {
const node = new Node(value);
node.next = this.first;
if(this.first) {
this.first.previous = node;
} else {
this.last = node;
}
this.first = node; // update head
this.size++;
return node;
}
(LinkedList.prototype.addFirst 的完整程式碼
註意,我們需要十分謹慎地更新節點的 previous 取用、雙向連結串列的 size 與雙向連結串列最後一個節點的取用。
removeFirst() {
const first = this.first;
if(first) {
this.first = first.next;
if(this.first) {
this.first.previous = null;
}
this.size--;
return first.value;
} else {
this.last = null;
}
}
(LinkedList.prototype.removeFirst 的完整程式碼
時間複雜度是什麼呢?
新增或刪除連結串列的最後一個元素
從雙向連結串列的末尾新增或刪除一個元素稍有點麻煩。當你查詢單向連結串列(操作的時間複雜度)時,這兩個操作都是 O(n),這是由於需要遍歷整條連結串列,直至找到最後一個元素。然而,雙向連結串列持有最後一個節點的取用:
addLast(value) {
const node = new Node(value);
if(this.first) {
node.previous = this.last;
this.last.next = node;
this.last = node;
} else {
this.first = node;
this.last = node;
}
this.size++;
return node;
}
(LinkedList.prototype.addLast 的完整程式碼)
同樣,我們需要小心地更新取用與處理一些特殊情況,如連結串列中只有一個元素時。
removeLast() {
let current = this.first;
let target;
if(current && current.next) {
target = this.last;
current = target.previous;
this.last = current;
current.next = null;
} else {
this.first = null;
this.last = null;
target = current;
}
if(target) {
this.size--;
return target.value;
}
}
(LinkedList.prototype.removeLast 的完整程式碼)
使用了雙向連結串列,我們不再需要遍歷整個連結串列直至找到倒數第二個元素。可以直接使用 this.last.previous 來找到它,時間複雜度是 O(1)。
下文將介紹佇列相關的知識,本文中佇列是使用兩個陣列實現的。可以改為使用雙向連結串列實現佇列,因為(雙向連結串列)新增首個元素與刪除最後一個元素時間複雜度都是 O(1)。
新增一個元素至連結串列任意一處
藉助 addFirst 與 addLast,可以實現將一個元素新增到連結串列任意一處,實現如下:
add(value, index = 0) {
if(index === 0) {
return this.addFirst(value);
}
for (let current = this.first, i = 0; i <= this.size; i++, current = (current && current.next)) {
if(i === index) {
if(i === this.size) { // if it doesn't have next it means that it is the last
return this.addLast(value);
}
const newNode = new Node(value);
newNode.previous = current.previous;
newNode.next = current;
current.previous.next = newNode;
if(current.next) { current.next.previous = newNode; }
this.size++;
return newNode;
}
}
}
(LinkedList.prototype.add 的完整程式碼)
如果新增元素的位置是在連結串列中間,我們就必須更新該元素前後節點的 next 與 previous 取用。
雙向連結串列方法的時間複雜度
雙向連結串列每個方法的時間複雜度如下表:
與單向鏈表相比,有了很大的改進(譯者註:其實看場景,不要盲目認為雙向連結串列一定比單向連結串列強)!(addLast 與 removeLast)操作時間複雜度從 O(n) 降至 O(1) ,這是由於:
-
新增對前一個節點的取用。
-
持有連結串列最後一個節點的取用。
刪除首個或最後一個節點可以在恆定時間內完成,然而刪除中間的節點時間複雜度仍然是 O(n)。
Stacks
棧是一種越後被新增的元素,越先被彈出的資料結構。也就是後進先出(LIFO).

讓我們從零開始實現一個棧!
class Stack {
constructor() {
this.input = [];
}
push(element) {
this.input.push(element);
return this;
}
pop() {
return this.input.pop();
}
}
正如你看到的,如果使用內建的 Array.push 與 Array.pop 實現一個棧,那是十分簡單的。兩個方法的時間複雜度都是 O(1)。
下麵來看看棧的具體使用:
const stack = new Stack();
stack.push('a');
stack.push('b');
stack.push('c');
stack.pop(); // c
stack.pop(); // b
stack.pop(); // a
最先被加入進去的元素 a 直到最後才被彈出。棧也可以透過連結串列來實現,對應方法的時間複雜度是一樣的。
這就是棧的全部內容啦!
Queues
佇列是一種越先被新增的元素,越先被出列的資料結構。也就是先進先出(FIFO)。就如現實中排成一條隊的人們一樣,先排隊的先被服務(也就是出列)。
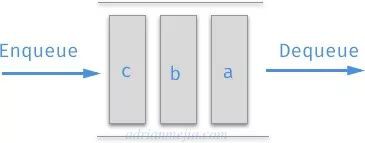
可以透過陣列來實現一個佇列,程式碼與棧的實現相類似。
透過陣列實現佇列
透過 Array.push 與 Array.shift 可以實現一個簡單(譯者註:即不是最優的實現方式)的佇列:
class Queue {
constructor() {
this.input = [];
}
add(element) {
this.input.push(element);
}
remove() {
return this.input.shift();
}
}
Queue.add 與 Queue.remove 的時間複雜度是什麼呢?
-
Queue.add 使用 Array.push 實現,可以在恆定時間內完成。這非常不錯!
-
Queue.remove 使用 Array.shift 實現,Array.shift 耗時是線性的(即 O(n))。我們可以減少 Queue.remove 的耗時嗎?
試想一下,如果只用 Array.push 與 Array.pop 能實現一個佇列嗎?
class Queue {
constructor() {
this.input = [];
this.output = [];
}
add(element) {
this.input.push(element);
}
remove() {
if(!this.output.length) {
while(this.input.length) {
this.output.push(this.input.pop());
}
}
return this.output.pop();
}
}
現在,我們使用兩個而不是一個陣列來實現一個佇列。
const queue = new Queue();
queue.add('a');
queue.add('b');
queue.remove() // a
queue.add('c');
queue.remove() // b
queue.remove() // c
當我們第一次執行出列操作時,output 陣列是空的,因此將 input 陣列的內容反向新增到 output 中,此時 output 的值是 [‘b’, ‘a’]。然後再從 output 中彈出元素。正如你所看到的,透過這個技巧實現的佇列,元素輸出的順序也是先進先出(FIFO)的。
那時間複雜度是什麼呢?
如果 output 陣列已經有元素了,那麼出列操作就是恆定的 O(1)。而當 output 需要被填充(即裡面沒有元素)時,時間複雜度變為 O(n)。output 被填充後,出列操作耗時再次變為恆定。因此分攤後是 O(1)。
也可以透過連結串列來實現佇列,相關操作耗時也是恆定的。下一節將帶來具體的實現。
透過雙向連結串列實現佇列
如果希望佇列有最好的效能,就需要透過雙向連結串列而不是陣列來實現(譯者註:並非陣列實現就完全不好,空間上雙向連結串列就不佔優勢,還是具體問題具體分析)。
const LinkedList = require('../linked-lists/linked-list');
class Queue {
constructor() {
this.input = new LinkedList();
}
add(element) {
this.input.addFirst(element);
}
remove() {
return this.input.removeLast();
}
get size() {
return this.input.size;
}
}
透過雙向連結串列實現的佇列,我們持有(雙向連結串列中)首個與最後一個節點的取用,因此入列與出列的時間複雜度都是 O(1)。這就是為遇到的問題選擇合適資料結構的重要性 ?。
總結
我們討論了大部分線性的資料結構。可以看出,根據實現方法的不同,相同的資料結構也會有不同的時間複雜度。
以下是本文討論內容的總結:
時間複雜度
* = 執行時分攤
註意: 二叉搜尋樹 與其他樹結構、圖結構,將在另一篇文章中討論。
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」,修煉程式設計內功
 知識星球
知識星球
