當然，我們本身不是為了加強條件而加強，而是因為在很多情況下，KL(p(x,z)‖q(x,z)) 或 KL(q(x,z)‖p(x,z)) 往往比 KL(p̃(x)‖q(x)) 更加容易計算。所以變分推斷是提供了一個可計算的方案。

VAE和EM演演算法

由上述關於變分推斷的新理解，我們可以在幾句話內匯出兩個基本結果：變分自編碼器和 EM 演演算法。這部分內容，實際上在從最大似然到EM演演算法：一致的理解方式和變分自編碼器（二）：從貝葉斯觀點出發已經詳細介紹過了。這裡用簡單幾句話重提一下。

VAE

在 VAE 中，我們設 q(x,z)=q(x|z)q(z),p(x,z)=p̃(x)p(z|x)，其中 q(x|z),p(z|x) 帶有未知引數的高斯分佈而 q(z) 是標準高斯分佈。最小化的標的是：

其中 logp̃(x) 沒有包含最佳化標的，可以視為常數，而對 p̃(x) 的積分則轉化為對樣本的取樣，從而：

因為 q(x|z),p(z|x) 為帶有神經網路的高斯分佈，這時候 KL(p(z|x)‖q(z)) 可以顯式地算出，而透過重引數技巧來取樣一個點完成積分 ∫p(z|x)logq(x|z)dz 的估算，可以得到 VAE 最終要最小化的 loss：

EM演演算法

在 VAE 中我們對後驗分佈做了約束，僅假設它是高斯分佈，所以我們最佳化的是高斯分佈的引數。如果不作此假設，那麼直接最佳化原始標的 (5)，在某些情況下也是可操作的，但這時候只能採用交替最佳化的方式：先固定 p(z|x)，最佳化 q(x|z)，那麼就有：

完成這一步後，我們固定 q(x,z)，最佳化 p(z|x)，先將 q(x|z)q(z) 寫成 q(z|x)q(x) 的形式：

那麼有：

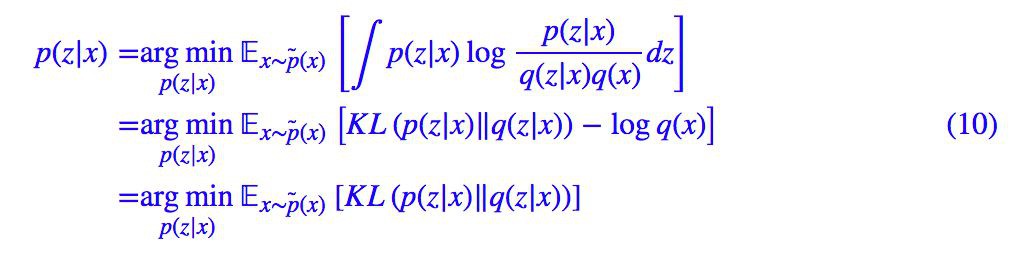
由於現在對 p(z|x) 沒有約束，因此可以直接讓 p(z|x)=q(z|x) 使得 loss 等於 0。也就是說，p(z|x) 有理論最優解：

(8)，(11) 的交替執行，構成了 EM 演演算法的求解步驟。這樣，我們從變分推斷框架中快速得到了 EM 演演算法。

變分推斷下的GAN

在這部分內容中，我們介紹了一般化的將 GAN 納入到變分推斷中的方法，這將引導我們得到 GAN 的新理解，以及一個有效的正則項。 

一般框架

同 VAE 一樣，GAN 也希望能訓練一個生成模型 q(x|z)，來將 q(z)=N(z;0,I) 對映為資料集分佈 p̃(x)，不同於 VAE 中將 q(x|z) 選擇為高斯分佈，GAN 的選擇是：

其中 δ(x) 是狄拉克 δ 函式，G(z) 即為生成器的神經網路。

一般我們會認為 z 是一個隱變數，但由於 δ 函式實際上意味著單點分佈，因此可以認為 x 與 z 的關係已經是一一對應的，所以 z 與 x 的關係已經“不夠隨機”，在 GAN 中我們認為它不是隱變數（意味著我們不需要考慮後驗分佈 p(z|x)）。

事實上，在 GAN 中僅僅引入了一個二元的隱變數 y 來構成聯合分佈：

這裡 p1=1−p0 描述了一個二元機率分佈，我們直接取 p1=p0=1/2。另一方面，我們設 p(x,y)=p(y|x)p̃(x)，p(y|x) 是一個條件伯努利分佈。而最佳化標的是另一方向的 KL(q(x,y)‖p(x,y))：

一旦成功最佳化，那麼就有 q(x,y)→p(x,y)，那麼：

從而 q(x)→p̃(x)，完成了生成模型的構建。 

現在我們最佳化物件有 p(y|x) 和 G(x)，記 p(1|x)=D(x)，這就是判別器。類似 EM 演演算法，我們進行交替最佳化：先固定 G(z)，這也意味著 q(x) 固定了，然後最佳化 p(y|x)，這時候略去常量，得到最佳化標的為：

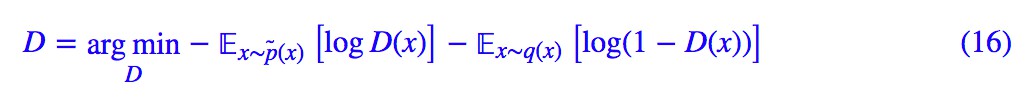
然後固定 D(x) 來最佳化 G(x)，這時候相關的 loss 為：

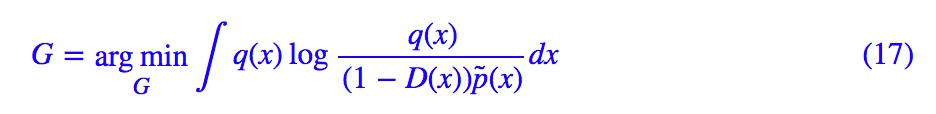
這裡包含了我們不知道的 p̃(x)，但是假如 D(x) 模型具有足夠的擬合能力，那麼跟 (11) 式同理，D(x) 的最優解應該是：

這裡的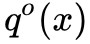是前一階段的 q(x)。從中解出 q̃(x)，代入 loss 得到：

基本分析

可以看到，第一項就是標準的 GAN 生成器所採用的 loss 之一。

多出來的第二項，描述了新分佈與舊分佈之間的距離。這兩項 loss 是對抗的，因為希望新舊分佈儘量一致，但是如果判別器充分最佳化的話，對於舊分佈中的樣本，D(x) 都很小（幾乎都被識別為負樣本），所以 −logD(x) 會相當大，反之亦然。這樣一來，整個 loss 一起最佳化的話，模型既要“傳承”舊分佈，同時要在往新方向 p(1|y) 探索，在新舊之間插值。

我們知道，目前標準的 GAN 的生成器 loss 都不包含，這事實上造成了 loss 的不完備。假設有一個最佳化演演算法總能找到 G(z) 的理論最優解、並且 G(z) 具有無限的擬合能力，那麼 G(z) 只需要生成唯一一個使得 D(x) 最大的樣本（不管輸入的 z 是什麼），這就是模型坍縮。這樣說的話，理論上它一定會發生。

那麼，給我們的啟發是什麼呢？我們設：

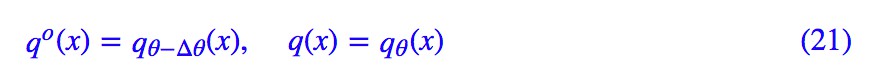
也就是說，假設當前模型的引數改變數為 Δθ，那麼展開到二階得到：

我們已經指出一個完備的 GAN 生成器的損失函式應該要包含，如果不包含的話，那麼就要透過各種間接手段達到這個效果，上述近似表明額外的損失約為 (Δθ⋅c)2，這就要求我們不能使得它過大，也就是不能使得 Δθ 過大（在每個階段 c 可以近似認為是一個常數）。

而我們用的是基於梯度下降的最佳化演演算法，所以 Δθ 正比於梯度，因此標準 GAN 訓練時的很多 trick，比如梯度裁剪、用 adam 最佳化器、用 BN，都可以解釋得通了，它們都是為了穩定梯度，使得 θ 不至於過大，同時，G(z) 的迭代次數也不能過多，因為過多同樣會導致 Δθ 過大。

還有，這部分的分析只適用於生成器，而判別器本身並不受約束，因此判別器可以訓練到最優。

正則項

現在我們從中算出一些真正有用的內容，直接對進行估算，以得到一個可以在實際訓練中使用的正則項。直接計算是難以進行的，但我們可以用 KL(q(x,z)‖q̃(x,z)) 去估算它：

因為有極限：

所以可以將 δ(x) 看成是小方差的高斯分佈，代入算得也就是我們有：

所以完整生成器的 loss 可以選為：

也就是說，可以用新舊生成樣本的距離作為正則項，正則項保證模型不會過於偏離舊分佈。

下麵的兩個在人臉資料 CelebA 上的實驗表明這個正則項是生效的。實驗程式碼修改自：

https://github.com/LynnHo/DCGAN-LSGAN-WGAN-WGAN-GP-Tensorflow

實驗一：普通的 DCGAN 網路，每次迭代生成器和判別器各訓練一個 batch。

▲ 不帶正則項，在25個epoch之後模型開始坍縮

▲ 帶有正則項，模型能一直穩定訓練

實驗二：普通的 DCGAN 網路，但去掉 BN，每次迭代生成器和判別器各訓練五個 batch。

▲ 不帶正則項，模型收斂速度比較慢

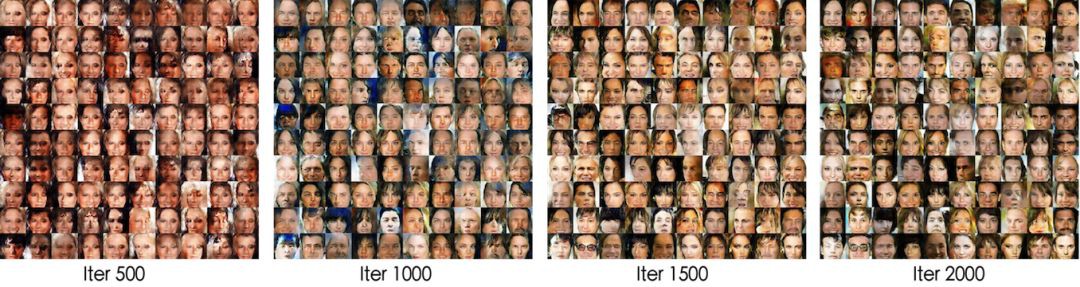
▲ 帶有正則項，模型更快“步入正軌”

GAN相關模型

對抗自編碼器（Adversarial Autoencoders，AAE）和對抗推斷學習（Adversarially Learned Inference，ALI）這兩個模型是 GAN 的變種之一，也可以被納入到變分推斷中。當然，有了前述準備後，這僅僅就像兩道作業題罷了。 

有意思的是，在 ALI 之中，我們有一些反直覺的結果。

GAN視角下的AAE

事實上，只需要在 GAN 的論述中，將 x,z 的位置交換，就得到了 AAE 的框架。 

具體來說，AAE 希望能訓練一個編碼模型 p(z|x)，來將真實分佈 q̃(x) 對映為標準高斯分佈 q(z)=N(z;0,I)，而：

其中 E(x) 即為編碼器的神經網路。

同 GAN 一樣，AAE 引入了一個二元的隱變數 y，並有：

同樣直接取 p1=p0=1/2。另一方面，我們設 q(z,y)=q(y|z)q(z)，這裡的後驗分佈 p(y|z) 是一個輸入為 z 的二元分佈，然後去最佳化 KL(p(z,y)‖q(z,y))：

現在我們最佳化物件有 q(y|z) 和 E(x)，記 q(0|z)=D(z)，依然交替最佳化：先固定 E(x)，這也意味著 p(z) 固定了，然後最佳化 q(y|z)，這時候略去常量，得到最佳化標的為：

然後固定 D(z) 來最佳化 E(x)，這時候相關的 loss 為：

利用 D(z) 的理論最優解，代入 loss 得到：

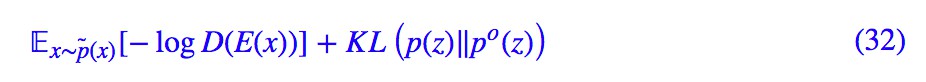
一方面，同標準 GAN 一樣，謹慎地訓練，我們可以去掉第二項，得到：

另外一方面，我們可以得到編碼器後再訓練一個解碼器 G(z)，但是如果所假設的 E(x),G(z) 的擬合能力是充分的，重構誤差可以足夠小，那麼將 G(z) 加入到上述 loss 中並不會幹擾 GAN 的訓練，因此可以聯合訓練：

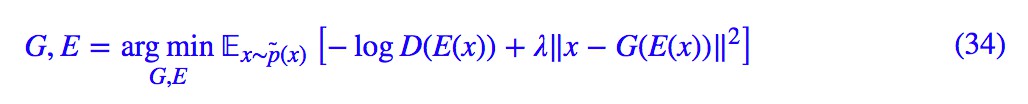
反直覺的ALI版本

ALI 像是 GAN 和 AAE 的融合，另一個幾乎一樣的工作是 Bidirectional GAN (BiGAN)。相比於 GAN，它將 z 也作為隱變數納入到變分推斷中。具體來說，在 ALI 中有：

以及 p(x,z,y)=p(y|x,z)p(z|x)p̃(x)，然後去最佳化 KL(q(x,z,y)‖p(x,z,y))：

等價於最小化：

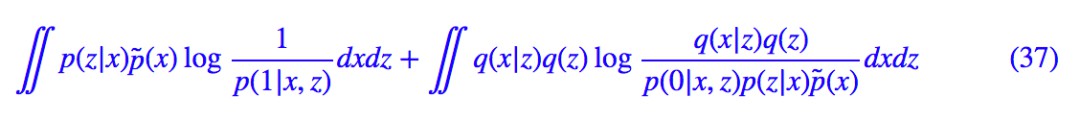
現在最佳化的物件有 p(y|x,z),p(z|x),q(x|z)，記 p(1|x,z)=D(x,z)，而 p(z|x) 是一個帶有編碼器E的高斯分佈或狄拉克分佈，q(x|z) 是一個帶有生成器 G 的高斯分佈或狄拉克分佈。依然交替最佳化：先固定 E,G，那麼與 D 相關的 loss 為：

跟 VAE 一樣，對 p(z|x) 和 q(x|z) 的期望可以透過“重引數”技巧完成。接著固定 D 來最佳化 G,E，因為這時候有 E 又有 G，整個 loss 沒得化簡，還是 (37) 那樣。但利用 D 的最優解：

可以轉化為：

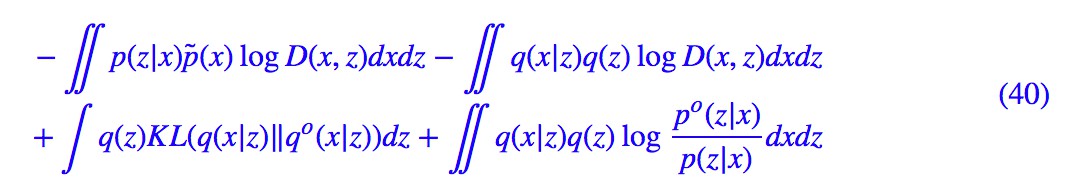
由於 q(x|z),p(x|z) 都是高斯分佈，事實上後兩項我們可以具體地算出來（配合重引數技巧），但同標準 GAN 一樣，謹慎地訓練，我們可以簡單地去掉後面兩項，得到：

這就是我們匯出的 ALI 的生成器和編碼器的 loss，它跟標準的 ALI 結果有所不同。標準的 ALI（包括普通的 GAN）將其視為一個極大極小問題，所以生成器和編碼器的 loss 為：

或：

它們都不等價於 (41)。針對這個差異，事實上筆者也做了實驗，結果表明這裡的 ALI 有著和標準的 ALI 同樣的表現，甚至可能稍好一些（可能是我的自我良好的錯覺，所以就沒有放圖了）。這說明，將對抗網路視為一個極大極小問題僅僅是一個直覺行為，並非總應該如此。

結論綜述

本文的結果表明瞭變分推斷確實是一個推導和解釋生成模型的統一框架，包括 VAE 和 GAN。透過變分推斷的新詮釋，我們介紹了變分推斷是如何達到這個目的的。 

當然，本文不是第一篇提出用變分推斷研究 GAN 這個想法的文章。在《On Unifying Deep Generative Models》一文中，其作者也試圖用變分推斷統一 VAE 和 GAN，也得到了一些啟發性的結果。但筆者覺得那不夠清晰。事實上，我並沒有完全讀懂這篇文章，我不大確定，這篇文章究竟是將 GAN 納入到了變分推斷中了，還是將 VAE 納入到了 GAN 中。相對而言，我覺得本文的論述更加清晰、明確一些。 

看起來變分推斷還有很大的挖掘空間，等待著我們去探索。