
作者丨龍心塵 & 寒小陽
研究方向丨機器學習,資料挖掘
題記:多年以後,當資深演演算法專家們看著無縫對接使用者需求的廣告收入節節攀升時,他們可能會想起自己之前痛苦推導 FM 與深度學習公式的某個夜晚……
本文程式碼部分參考了 lambda 等同學的 TensorFlow 實現,在此向原作者表示感謝。
引言
點選率(click-through rate, CTR)是網際網路公司進行流量分配的核心依據之一。比如網際網路廣告平臺,為了精細化權衡和保障使用者、廣告、平臺三方的利益,準確的 CTR 預估是不可或缺的。CTR 預估技術從傳統的邏輯回歸,到近兩年大火的深度學習,新的演演算法層出不窮:DeepFM, NFM, DIN, AFM, DCN……
然而,相關的綜述文章不少,但碎片羅列的居多,模型之間內在的聯絡和演化思路如何揭示?怎樣才能迅速 get 到新模型的創新點和適用場景,快速提高新論文速度,節約理解、復現模型的成本?這些都是亟待解決的問題。
我們認為,從 FM 及其與神經網路的結合出發,能夠迅速貫穿很多深度學習 CTR 預估網路的思路,從而更好地理解和應用模型。
本文的思路與方法
1. 我們試圖從原理上進行推導、理解各個深度 CTR 預估模型之間的相互關係,知其然也知其所以然(以下的分析與拆解角度,是一種我們嘗試的理解視角,並不是唯一的理解方式)。
2. 推演的核心思路:“透過設計網路結構進行組合特徵的挖掘”。
3. 具體來說有兩條:其一是從 FM 開始推演其在深度學習上的各種推廣(對應下圖的紅線),另一條是從 embedding + MLP 自身的演進特點結合 CTR 預估本身的業務場景進行推演(對應下圖黑線部分)。

4. 為了便於理解,我們簡化了資料案例——只考慮離散特徵資料的建模,以分析不同神經網路在處理相同業務問題時的不同思路。
5. 同時,我們將各典型論文不同風格的神經網路結構圖統一按照計算圖來繪製,以便於對比不同模型。
FM:降維版本的特徵二階組合
CTR 預估本質是一個二分類問題,以移動端展示廣告推薦為例,依據日誌中的使用者側的資訊(比如年齡,性別,國籍,手機上安裝的 app 串列)、廣告側的資訊(廣告 id,廣告類別,廣告標題等)、背景關係側資訊(渠道 id 等),去建模預測使用者是否會點選該廣告。
FM 出現之前的傳統的處理方法是人工特徵工程加上線性模型(如邏輯回歸 Logistic Regression)。為了提高模型效果,關鍵技術是找到到使用者點選行為背後隱含的特徵組合。如男性、大學生使用者往往會點選遊戲類廣告,因此“男性且是大學生且是遊戲類”的特徵組合就是一個關鍵特徵。但這本質仍是線性模型,其假設函式表示成內積形式一般為:
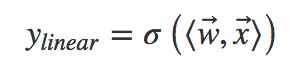
其中![]() 為特徵向量,
為特徵向量,![]() 為權重向量,σ() 為 sigmoid 函式。
為權重向量,σ() 為 sigmoid 函式。
但是人工進行特徵組合通常會存在諸多困難,如特徵爆炸、特徵難以被識別、組合特徵難以設計等。為了讓模型自動地考慮特徵之間的二階組合資訊,線性模型推廣為二階多項式(2d−Polynomial)模型:

其實就是對特徵兩兩相乘(組合)構成新特徵(離散化之後其實就是“且”操作),並對每個新特徵分配獨立的權重,透過機器學習來自動得到這些權重。將其寫成矩陣形式為:
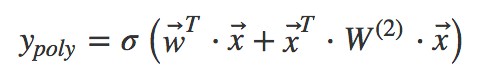
其中 為二階特徵組合的權重矩陣,是對稱矩陣。而這個矩陣引數非常多,為
為二階特徵組合的權重矩陣,是對稱矩陣。而這個矩陣引數非常多,為 。為了降低該矩陣的維度,可以將其因子分解(Factorization)為兩個低維(比如 n∗k)矩陣的相乘。則此時 W 矩陣的引數就大幅降低,為O(nk)。公式如下:
。為了降低該矩陣的維度,可以將其因子分解(Factorization)為兩個低維(比如 n∗k)矩陣的相乘。則此時 W 矩陣的引數就大幅降低,為O(nk)。公式如下:
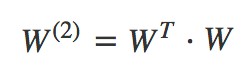
這就是 Rendle 等在 2010 年提出因子分解機(Factorization Machines,FM)的名字的由來。FM 的矩陣形式公式如下:
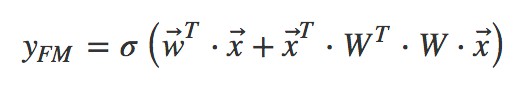
將其寫成內積的形式:

利用 ,可以將上式進一步改寫成求和式的形式:
,可以將上式進一步改寫成求和式的形式:
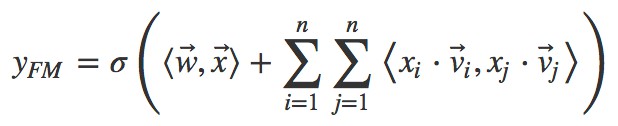
其中![]() 向量是矩陣 W 的第 i 列。為了去除重覆項與特徵平方項,上式可以進一步改寫成更為常見的 FM 公式:
向量是矩陣 W 的第 i 列。為了去除重覆項與特徵平方項,上式可以進一步改寫成更為常見的 FM 公式:
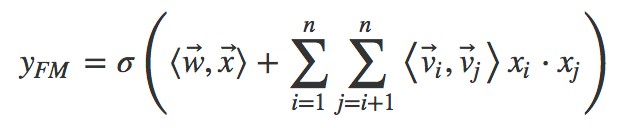
對比二階多項式模型,FM 模型中特徵兩兩相乘(組合)的權重是相互不獨立的,它是一種引數較少但表達力強的模型。
此處附上 FM 的 TensorFlow 程式碼實現,完整資料和程式碼請參考網盤。
網盤連結:
https://pan.baidu.com/s/1eDwOxweRDPurI2fF51EALQ
註意 FM 透過內積進行無重覆項與特徵平方項的特徵組合過程使用了一個小 trick,就是:

class FM(Model):
def __init__(self, input_dim=None, output_dim=1, factor_order=10, init_path=None, opt_algo='gd', learning_rate=1e-2,
l2_w=0, l2_v=0, random_seed=None):
Model.__init__(self)
# 一次、二次交叉、偏置項
init_vars = [('w', [input_dim, output_dim], 'xavier', dtype),
('v', [input_dim, factor_order], 'xavier', dtype),
('b', [output_dim], 'zero', dtype)]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = tf.sparse_placeholder(dtype)
self.y = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w = self.vars['w']
v = self.vars['v']
b = self.vars['b']
# [(x1+x2+x3)^2 - (x1^2+x2^2+x3^2)]/2
# 先計算所有的交叉項,再減去平方項(自己和自己相乘)
X_square = tf.SparseTensor(self.X.indices, tf.square(self.X.values), tf.to_int64(tf.shape(self.X)))
xv = tf.square(tf.sparse_tensor_dense_matmul(self.X, v))
p = 0.5 * tf.reshape(
tf.reduce_sum(xv - tf.sparse_tensor_dense_matmul(X_square, tf.square(v)), 1),
[-1, output_dim])
xw = tf.sparse_tensor_dense_matmul(self.X, w)
logits = tf.reshape(xw + b + p, [-1])
self.y_prob = tf.sigmoid(logits)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=self.y)) + \
l2_w * tf.nn.l2_loss(xw) + \
l2_v * tf.nn.l2_loss(xv)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
#GPU設定
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
# 圖中所有variable初始化
tf.global_variables_initializer().run(session=self.sess)用神經網路的視角看FM:嵌入後再進行內積
我們觀察 FM 公式的矩陣內積形式:
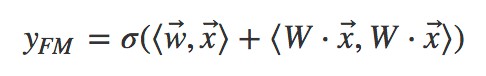
發現 部分就是將離散繫數特徵透過矩陣乘法降維成一個低維稠密向量。這個過程對神經網路來說就叫做嵌入(embedding)。所以用神經網路視角來看:
部分就是將離散繫數特徵透過矩陣乘法降維成一個低維稠密向量。這個過程對神經網路來說就叫做嵌入(embedding)。所以用神經網路視角來看:
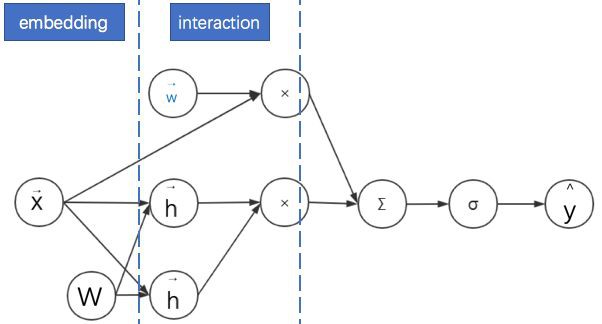
1. FM 首先是對離散特徵進行嵌入。
2. 之後透過對嵌入後的稠密向量進行內積來進行二階特徵組合。
3. 最後再與線性模型的結果求和進而得到預估點選率。
其示意圖如下。為了表述清晰,我們繪製的是神經網路計算圖而不是網路結構圖——在網路結構圖中增加了權重 W 的位置。
FM的實際應用:考慮領域資訊
廣告點選率預估模型中的特徵以分領域的離散特徵為主,如:廣告類別、使用者職業、手機APP串列等。由於連續特徵比較好處理,為了簡化起見,本文只考慮同時存在不同領域的離散特徵的情形。
處理離散特徵的常見方法是透過獨熱(one-hot)編碼轉換為一系列二值特徵向量。然後將這些高維稀疏特徵透過嵌入(embedding)轉換為低維連續特徵。前面已經說明 FM 中間的一個核心步驟就是嵌入,但這個嵌入過程沒有考慮領域資訊。這使得同領域內的特徵也被當做不同領域特徵進行兩兩組合了。
其實可以將特徵具有領域關係的特點作為先驗知識加入到神經網路的設計中去:同領域的特徵嵌入後直接求和作為一個整體嵌入向量,進而與其他領域的整體嵌入向量進行兩兩組合。而這個先嵌入後求和的過程,就是一個單領域的小離散特徵向量乘以矩陣的過程。
此時 FM 的過程變為:對不同領域的離散特徵分別進行嵌入,之後再進行二階特徵的向量內積。其計算圖圖如下所示:

這樣考慮其實是給 FM 增加了一個正則:考慮了領域內的資訊的相似性。而且還有一個附加的好處,這些嵌入後的同領域特徵可以拼接起來作為更深的神經網路的輸入,達到降維的目的。接下來我們將反覆看到這種處理方式。
此處需要註意,這與“基於領域的因子分解機”(Field-aware Factorization Machines,FFM)有區別。FFM 也是 FM 的另一種變體,也考慮了領域資訊。但其不同點是同一個特徵與不同領域進行特徵組合時,其對應的嵌入向量是不同的。本文不考慮 FFM 的作用機制。
經過這些改進的 FM 終究還是淺層網路,它的表現力仍然有限。為了增加模型的表現力(model capacity),一個自然的想法就是將該淺層網路不斷“深化”。
embedding+MLP:深度學習CTR預估的通用框架
embedding+MLP 是對於分領域離散特徵進行深度學習 CTR 預估的通用框架。深度學習在特徵組合挖掘(特徵學習)方面具有很大的優勢。比如以 CNN 為代表的深度網路主要用於影象、語音等稠密特徵上的學習,以 W2V、RNN 為代表的深度網路主要用於文字的同質化、序列化高維稀疏特徵的學習。CTR 預估的主要場景是對離散且有具體領域的特徵進行學習,所以其深度網路結構也不同於 CNN 與 RNN。
具體來說, embedding+MLP 的過程如下:
1. 對不同領域的 one-hot 特徵進行嵌入(embedding),使其降維成低維度稠密特徵。
2. 然後將這些特徵向量拼接(concatenate)成一個隱含層。
3. 之後再不斷堆疊全連線層,也就是多層感知機(Multilayer Perceptron, MLP,有時也叫作前饋神經網路)。
4. 最終輸出預測的點選率。
其示意圖如下:

embedding+MLP 的缺點是隻學習高階特徵組合,對於低階或者手動的特徵組合不夠相容,而且引數較多,學習較困難。
FNN:FM與MLP的串聯結合
Weinan Zhang 等在 2016 年提出的因子分解機神經網路(Factorisation Machine supported Neural Network,FNN)將考 FM 與 MLP 進行了結合。它有著十分顯著的特點:
1. 採用 FM 預訓練得到的隱含層及其權重作為神經網路的第一層的初始值,之後再不斷堆疊全連線層,最終輸出預測的點選率。
2. 可以將 FNN 理解成一種特殊的 embedding+MLP,其要求第一層嵌入後的各領域特徵維度一致,並且嵌入權重的初始化是 FM 預訓練好的。
3. 這不是一個端到端的訓練過程,有貪心訓練的思路。而且如果不考慮預訓練過程,模型網路結構也沒有考慮低階特徵組合。
其計算圖如下所示:

透過觀察 FFN 的計算圖可以看出其與 embedding+MLP 確實非常像。不過此處省略了 FNN 的 FM 部分的線性模組。這種省略為了更好地進行兩個模型的對比。接下來的計算圖我們都會省略線性模組。
此處附上 FNN 的程式碼實現,完整資料和程式碼請參考網盤。
網盤連結:
https://pan.baidu.com/s/1eDwOxweRDPurI2fF51EALQ
class FNN(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
node_in = num_inputs * embed_size
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
l = xw
#全連線部分
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
print(l.shape, wi.shape, bi.shape)
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
NFM:透過逐元素乘法延遲FM的實現過程
我們再回到考慮領域資訊的 FM,它仍有改進的空間。因為以上這些網路的 FM 部分都是隻進行嵌入向量的兩兩內積後直接求和,沒有充分利用二階特徵組合的資訊。Xiangnan He 等在 2017 年提出了神經網路因子分解機(Neural Factorization Machines,NFM)對此作出了改進。其計算圖如下所示:

NFM 的基本特點是:
1. 利用二階互動池化層(Bi-Interaction Pooling)對 FM 嵌入後的向量兩兩進行元素級別的乘法,形成同維度的向量求和後作為前饋神經網路的輸入。計算圖中用圈乘 ⨂ 表示逐元素乘法運算。
2. NFM 與 DeepFM 的區別是沒有單獨的 FM 的淺層網路進行聯合訓練,而是將其整合後直接輸出給前饋神經網路。
3. 當 MLP 的全連線層都是恆等變換且最後一層引數全為 1 時,NFM 就退化成了 FM。可見,NFM 是 FM 的推廣,它推遲了 FM 的實現過程,併在其中加入了更多非線性運算。
4. 另一方面,我們觀察計算圖會發現 NFM 與 FNN 非常相似。它們的主要區別是 NFM 在 embedding 之後對特徵進行了兩兩逐元素乘法。因為逐元素相乘的向量維數不變,之後對這些向量求和的維數仍然與 embedding 的維數一致。因此輸入到 MLP 的引數比起直接 concatenate 的 FNN 更少。
此處附上 NFM 的程式碼實現,完整資料和程式碼請參考網盤:
網盤連結:
https://pan.baidu.com/s/1eDwOxweRDPurI2fF51EALQ
def model_fn(features, labels, mode, params):
"""Bulid Model function f(x) for Estimator."""
#------hyperparameters----
field_size = params["field_size"]
feature_size = params["feature_size"]
embedding_size = params["embedding_size"]
l2_reg = params["l2_reg"]
learning_rate = params["learning_rate"]
#optimizer = params["optimizer"]
layers = map(int, params["deep_layers"].split(','))
dropout = map(float, params["dropout"].split(','))
#------bulid weights------
Global_Bias = tf.get_variable(name='bias', shape=[1], initializer=tf.constant_initializer(0.0))
Feat_Bias = tf.get_variable(name='linear', shape=[feature_size], initializer=tf.glorot_normal_initializer())
Feat_Emb = tf.get_variable(name='emb', shape=[feature_size,embedding_size], initializer=tf.glorot_normal_initializer())
#------build feaure-------
feat_ids = features['feat_ids']
feat_ids = tf.reshape(feat_ids,shape=[-1,field_size])
feat_vals = features['feat_vals']
feat_vals = tf.reshape(feat_vals,shape=[-1,field_size])
#------build f(x)------
with tf.variable_scope("Linear-part"):
feat_wgts = tf.nn.embedding_lookup(Feat_Bias, feat_ids) # None * F * 1
y_linear = tf.reduce_sum(tf.multiply(feat_wgts, feat_vals),1)
with tf.variable_scope("BiInter-part"):
embeddings = tf.nn.embedding_lookup(Feat_Emb, feat_ids) # None * F * K
feat_vals = tf.reshape(feat_vals, shape=[-1, field_size, 1])
embeddings = tf.multiply(embeddings, feat_vals) # vij * xi
sum_square_emb = tf.square(tf.reduce_sum(embeddings,1))
square_sum_emb = tf.reduce_sum(tf.square(embeddings),1)
deep_inputs = 0.5*tf.subtract(sum_square_emb, square_sum_emb) # None * K
with tf.variable_scope("Deep-part"):
if mode == tf.estimator.ModeKeys.TRAIN:
train_phase = True
else:
train_phase = False
if mode == tf.estimator.ModeKeys.TRAIN:
deep_inputs = tf.nn.dropout(deep_inputs, keep_prob=dropout[0]) # None * K
for i in range(len(layers)):
deep_inputs = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=layers[i], \
weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='mlp%d' % i)
if FLAGS.batch_norm:
deep_inputs = batch_norm_layer(deep_inputs, train_phase=train_phase, scope_bn='bn_%d' %i) #放在RELU之後 https://github.com/ducha-aiki/caffenet-benchmark/blob/master/batchnorm.md#bn----before-or-after-relu
if mode == tf.estimator.ModeKeys.TRAIN:
deep_inputs = tf.nn.dropout(deep_inputs, keep_prob=dropout[i]) #Apply Dropout after all BN layers and set dropout=0.8(drop_ratio=0.2)
#deep_inputs = tf.layers.dropout(inputs=deep_inputs, rate=dropout[i], training=mode == tf.estimator.ModeKeys.TRAIN)
y_deep = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=1, activation_fn=tf.identity, \
weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='deep_out')
y_d = tf.reshape(y_deep,shape=[-1])
with tf.variable_scope("NFM-out"):
#y_bias = Global_Bias * tf.ones_like(labels, dtype=tf.float32) # None * 1 warning;這裡不能用label,否則呼叫predict/export函式會出錯,train/evaluate正常;初步判斷estimator做了最佳化,用不到label時不傳
y_bias = Global_Bias * tf.ones_like(y_d, dtype=tf.float32) # None * 1
y = y_bias + y_linear + y_d
pred = tf.sigmoid(y)
predictions={"prob": pred}
export_outputs = {tf.saved_model.signature_constants.DEFAULT_SERVING_SIGNATURE_DEF_KEY: tf.estimator.export.PredictOutput(predictions)}
# Provide an estimator spec for `ModeKeys.PREDICT`
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
export_outputs=export_outputs)
#------bulid loss------
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=y, labels=labels)) + \
l2_reg * tf.nn.l2_loss(Feat_Bias) + l2_reg * tf.nn.l2_loss(Feat_Emb)
# Provide an estimator spec for `ModeKeys.EVAL`
eval_metric_ops = {
"auc": tf.metrics.auc(labels, pred)
}
if mode == tf.estimator.ModeKeys.EVAL:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=loss,
eval_metric_ops=eval_metric_ops)
#------bulid optimizer------
if FLAGS.optimizer == 'Adam':
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate, beta1=0.9, beta2=0.999, epsilon=1e-8)
elif FLAGS.optimizer == 'Adagrad':
optimizer = tf.train.AdagradOptimizer(learning_rate=learning_rate, initial_accumulator_value=1e-8)
elif FLAGS.optimizer == 'Momentum':
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.95)
elif FLAGS.optimizer == 'ftrl':
optimizer = tf.train.FtrlOptimizer(learning_rate)
train_op = optimizer.minimize(loss, global_step=tf.train.get_global_step())
# Provide an estimator spec for `ModeKeys.TRAIN` modes
if mode == tf.estimator.ModeKeys.TRAIN:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=loss,
train_op=train_op)AFM:對簡化版NFM進行加權求和
NFM 的主要創新點是在 FM 過程中添加了逐元素相乘的運算來增加模型的複雜度。但沒有在此基礎上新增更複雜的運算過程,比如對加權求和。Jun Xiao 等在 2017 年提出了註意力因子分解模型(Attentional Factorization Machine,AFM)就是在這個方向上的改進。其計算圖如下所示:

AFM 的特點是:
1. AFM 與 NFM 都是致力於充分利用二階特徵組合的資訊,對嵌入後的向量兩兩進行逐元素乘法,形成同維度的向量。而且 AFM 沒有 MLP 部分。
2. AFM 透過在逐元素乘法之後形成的向量進行加權求和,而且權重是基於網路自身來產生的。其方法是引入一個註意力子網路(Attention Net)。
3. 當權重都相等時,AFM 退化成無全連線層的 NFM。
4. “註意力子網路”的主要操作是進行矩陣乘法,其最終輸出結果為 softmax,以保證各分量的權重本身是一個機率分佈。
PNN:透過改進向量乘法運算延遲FM的實現過程
再回到 FM。既然 AFM、NFM 可以透過新增逐元素乘法的運算來增加模型的複雜度,那向量乘法有這麼多,可否用其他的方法增加 FM 複雜度?答案是可以的。Huifeng Guo 等在 2016 年提出了基於向量積的神經網路(Product-based Neural Networks,PNN)就是一個典型例子。其簡化計算圖如下所示:
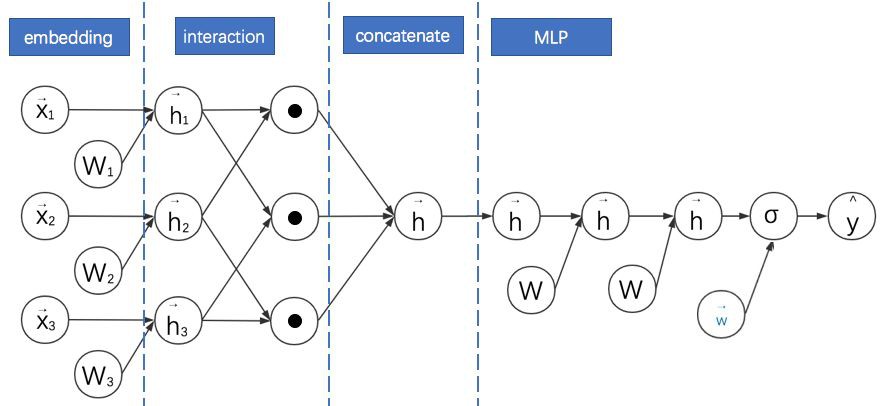
對比之前模型的計算圖,我們可以發現 PNN 的基本特點是:
1. 利用二階向量積層(Pair-wisely Connected Product Layer)對 FM 嵌入後的向量兩兩進行向量積,形成的結果作為之後 MLP 的輸入。計算圖中用圓點 • 表示向量積運算。PNN 採用的向量積有內積與外積兩種形式。
3. 需要說明的是,本計算圖中省略了 PNN 中向量與常數 1 進行的乘法運算。這部分其實與 FNN 類似,不是 PNN 的主要創新點。故在此圖中省略。
3. 對於內積形式的 PNN,因為兩個向量相乘的結果為標量,可以直接把各個標量“拼接”成一個大向量,就可以作為 MLP 的輸入了。
4. 當 MLP 的全連線層都是恆等變換且最後一層引數全為 1 時,內積形式的 PNN 就退化成了 FM。
5. 對於外積形式的 PNN,因為兩個向量相乘相當於列向量與行向量進行矩陣相乘,得到的結果為一個矩陣。各個矩陣向之前內積形式的操作一樣直接拼接起來維數太多,論文的簡化方案是直接對各個矩陣進行求和,得到的新矩陣(可以理解成之後對其拉長成向量)就直接作為 MLP 的輸入。
6. 觀察計算圖發現外積形式的 PNN 與 NFM 很像,其實就是 PNN 把 NFM 的逐元素乘法換成了外積。
此處分別附上 PNN 的內積與外積形式程式碼,完整資料和程式碼請參考網盤。
網盤連結:
https://pan.baidu.com/s/1eDwOxweRDPurI2fF51EALQ
DCN:高階FM的降維實現
以上的 FM 推廣形式,主要是對 FM 進行二階特徵組合。高階特徵組合是透過 MLP 實現的。但這兩種實現方式是有很大不同的,FM 更多是透過向量 embedding 之間的內積來實現,而 MLP 則是在向量 embedding 之後一層一層進行權重矩陣乘法實現。可否直接將 FM 的過程在高階特徵組合上進行推廣?答案是可以的。Ruoxi Wang 等在 2017 提出的深度與交叉神經網路(Deep & Cross Network,DCN)就是在這個方向進行改進的。DCN 的計算圖如下:

DCN 的特點如下:
1. Deep 部分就是普通的 MLP 網路,主要是全連線。
2. 與 DeepFM 類似,DCN 是由 embedding + MLP 部分與 cross 部分進行聯合訓練的。Cross 部分是對 FM 部分的推廣。
3. Cross 部分的公式如下:


4. 可以證明,cross 網路是 FM 的過程在高階特徵組合的推廣。完全的證明需要一些公式推導,感興趣的同學可以直接參考原論文的附錄。
5. 而用簡單的公式證明可以得到一個很重要的結論:只有兩層且第一層與最後一層權重引數相等時的 Cross 網路與簡化版 FM 等價。
6. 此處對應簡化版的 FM 視角是將拼接好的稠密向量作為輸入向量,且不做領域方面的區分(但產生這些稠密向量的過程是考慮領域資訊的,相對全特徵維度的全連線層減少了大量引數,可以視作稀疏連結思想的體現)。而且之後進行 embedding 權重矩陣 W 只有一列——是退化成列向量的情形。
7. 與 MLP 網路相比,Cross 部分在增加高階特徵組合的同時減少了引數的個數,並省去了非線性啟用函式。
Wide&Deep;:DeepFM與DCN的基礎框架
開篇已經提到,本文思路有兩條主線。到此為止已經將基於 FM 的主線介紹基本完畢。接下來將串講從 embedding+MLP 自身的演進特點的 CTR 預估模型主線,而這條思路與我們之前的 FM 思路同樣有千絲萬縷的聯絡。
Google 在 2016 年提出的寬度與深度模型(Wide&Deep;)在深度學習 CTR 預估模型中佔有非常重要的位置,它奠定了之後基於深度學習的廣告點選率預估模型的框架。
Wide&Deep;將深度模型與線性模型進行聯合訓練,二者的結果求和輸出為最終點選率。其計算圖如下:

我們將 Wide&Deep; 的計算圖與之前的模型進行對比可知:
1. Wide&Deep; 是前面介紹模型 DeepFM 與 DCN 的基礎框架。這些模型均採用神經網路聯合訓練的思路,對神經網路進行並聯。
2. DeepFM、DCN 與 Wide&Deep; 的 Deep 部分都是 MLP。
3. Wide&Deep; 的 Wide 部分是邏輯回歸,可以手動設計組合特徵。
4. DeepFM 的 Wide 部分是 FM,DCN 的 Wide 部分是 Cross 網路,二者均不強求手動設計特徵。但此時都與字面意義上的 Wide 有一定差異,因為均共享了降維後的嵌入特徵。
此處附上 DeepFM 的程式碼實現,完整資料和程式碼請參考網盤:
網盤連結:
https://pan.baidu.com/s/1eDwOxweRDPurI2fF51EALQ
def get_model(model_type, model_dir):
print("Model directory = %s" % model_dir)
# 對checkpoint去做設定
runconfig = tf.contrib.learn.RunConfig(
save_checkpoints_secs=None,
save_checkpoints_steps = 100,
)
m = None
# 寬模型
if model_type == 'WIDE':
m = tf.contrib.learn.LinearClassifier(
model_dir=model_dir,
feature_columns=wide_columns)
# 深度模型
if model_type == 'DEEP':
m = tf.contrib.learn.DNNClassifier(
model_dir=model_dir,
feature_columns=deep_columns,
hidden_units=[100, 50, 25])
# 寬度深度模型
if model_type == 'WIDE_AND_DEEP':
m = tf.contrib.learn.DNNLinearCombinedClassifier(
model_dir=model_dir,
linear_feature_columns=wide_columns,
dnn_feature_columns=deep_columns,
dnn_hidden_units=[100, 70, 50, 25],
config=runconfig)
print('estimator built')
return mDeep Cross:DCN由其殘差網路思想進化
由 K. He 等提出的深度殘差網路能夠大大加深神經網路的深度,同時不會引起退化的問題,顯著提高了模型的精度。Ying Shan 等將該思路應用到廣告點選率預估模型中,提出深度交叉模型(DeepCross,2016)。Deep Cross 的計算圖如下:
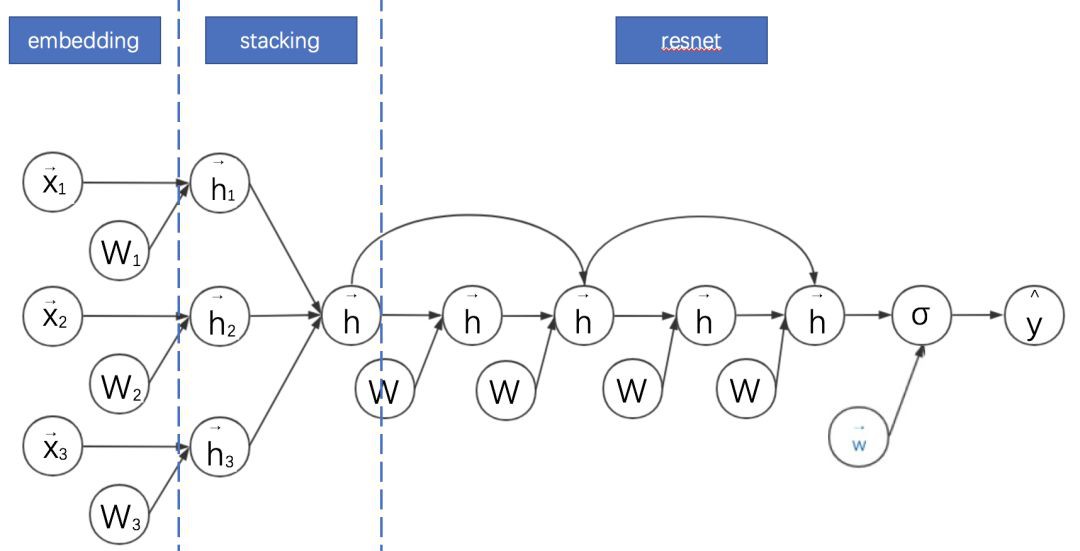
將 Deep Cross 與之前的模型對比,可以發現其特點是:
1. 對 embedding+MLP 的改進主要是 MLP 部分增加跳躍連線成為殘差網路。
2. Deep Cross 與傳統的殘差網路的區別主要是沒有採用摺積操作。其中一個原因是在廣告點選率預估領域,特徵不具備平移不變性。
3. DCN 其實是從 Deep Cross 進化出來的版本。DCN 相對 Deep Cross 的主要貢獻是解耦了 Deep 與 Cross(特徵交叉)部分。
4. 因此 DCN 中的 Cross 部分可以理解為殘差網路的變體:其將 Deep Cross 的跨越連結縮短為只有一層,而全連線部分改為與權重向量和輸入向量的內積。
DIN:對同領域歷史資訊引入註意力機制的MLP
以上神經網路對同領域離散特徵的處理基本是將其嵌入後直接求和,這在一般情況下沒太大問題。但其實可以做得更加精細。
比如對於歷史統計類特徵。以使用者歷史瀏覽的商戶 id 為例,假設使用者歷史瀏覽了 10 個商戶,這些商戶 id 的常規處理方法是作為同一個領域的特徵嵌入後直接求和得到一個嵌入向量。但這 10 個商戶只有一兩個商戶與當前被預測的廣告所在的商戶相似,其他商戶關係不大。增加這兩個商戶在求和過程中的權重,應該能夠更好地提高模型的表現力。而增加求和權重的思路就是典型的註意力機制思路。
由 Bahdanau et al. (2015) 引入的現代註意力機制,本質上是加權平均(權重是模型根據資料學習出來的),其在機器翻譯上應用得非常成功。受註意力機制的啟發,Guorui Zhou 等在 2017 年提出了深度興趣網路(Deep Interest Network,DIN)。DIN 主要關註使用者在同一領域的歷史行為特徵,如瀏覽了多個商家、多個商品等。DIN 可以對這些特徵分配不同的權重進行求和。其網路結構圖如下:

1. 此處採用原論文的結構圖,表示起來更清晰。
2. DIN 考慮對同一領域的歷史特徵進行加權求和,以加強其感興趣的特徵的影響。
3. 使用者的每個領域的歷史特徵權重則由該歷史特徵及其對應備選廣告特徵透過一個子網路得到。即使用者歷史瀏覽的商戶特徵與當前瀏覽商戶特徵對應,歷史瀏覽的商品特徵與當前瀏覽商品特徵對應。
4. 權重子網路主要包括特徵之間的元素級別的乘法、加法和全連線等操作。
5. AFM 也引入了註意力機制。但是 AFM 是將註意力機制與 FM 同領域特徵求和之後進行結合,DIN 直接是將註意力機制與同領域特徵求和之前進行結合。
多工視角:資訊的遷移與補充
對於資料驅動的解決方案而言,資料和模型同樣重要,資料(特徵)通常決定了效果的上限,各式各樣的模型會以不同的方式去逼近這個上限。而所有演演算法應用的老司機都知道很多場景下,如果有更多的資料進行模型訓練,效果一般都能顯著得到提高。
廣告也是一樣的場景,在很多電商的平臺上會有很多不同場景的廣告位,每個場景蘊含了使用者的不同興趣的表達,這些資訊的彙總與融合可以帶來最後效果的提升。但是將不同場景的資料直接進行合併用來訓練(ctr/cvr)模型,結果很多時候並不是很樂觀,仔細想想也是合理的,不同場景下的樣本分佈存在差異,直接對樣本累加會影響分佈導致效果負向。

而深度學習發展,使得資訊的融合與應用有了更好的進展,用 Multi−task learning (MTL)的方式可以很漂亮的解決上面提到的問題。我們不直接對樣本進行累加和訓練,而是像上圖所示,把兩個場景分為兩個 task,即分為兩個子網路。
對單個網路而言,底層的 embedding 層的表達受限於單場景的資料量,很可能學習不充分。而上圖這樣的網路結合,使得整個訓練過程有了表示學習的共享(Shared Lookup Table),這種共享有助於大樣本的子任務幫助小樣本的子任務,使得底層的表達學習更加充分。
DeepFM 和 DCN 也用到了這個思路!只是它們是對同一任務的不同模型進行結合,而多工學習是對不同任務的不同模型進行結合。而且,我們可以玩得更加複雜。
Multi-task learning (MTL) 整個結構的上層的不同的 task 的子網路是不一樣的,這樣每個子網路可以各自去擬合自己 task 對應的概念分佈。並且,取決於問題與場景的相似性和複雜度,可以把底層的表達學習,從簡單的共享 embedding 到共享一些層次的表達。極端的情況是我們可以直接共享所有的表達學習(representation learning)部分,而只接不同的網路 head 來完成不一樣的任務。這樣帶來的另外一個好處是,不同的task 可以共享一部分計算,從而實現計算的加速。
值得一提的另一篇 paper 是阿裡媽媽團隊提出的“完整空間多工模型”(Entire Space Multi-Task Model,ESMM),也是很典型的多工學習和資訊補充思路,這篇 paper 解決的問題不是 CTR(點選率)預估而是 CVR(轉化率)預估,傳統 CVR 預估模型會有比較明顯的樣本選擇偏差(sample selection bias)和訓練資料過於稀疏(data sparsity)的問題,而 ESMM 模型利用使用者行為序列資料,在完整的樣本資料空間同時學習點選率和轉化率(post-view clickthrough&conversion; rate,CTCVR),在一定程度上解決了這個問題。
在電商的場景下,使用者的決策過程很可能是這樣的,在觀察到系統展現的推薦商品串列後,點選自己感興趣的商品,進而產生購買行為。所以使用者行為遵循這樣一個決策順序:impression → click → conversion。CVR 模型旨在預估使用者在觀察到曝光商品進而點選到商品詳情頁之後購買此商品的機率,即 pCVR = p (conversion|click, impression)。
預估點選率 pCTR,預估點選下單率 pCVR 和預估點選與下單率 pCTCVR 關係如下。

傳統的 CVR 預估任務通常採用類似於 CTR 預估的技術進行建模。但是不同於 CTR 預估任務的是,這個場景面臨一些特有的挑戰:1) 樣本選擇偏差;2) 訓練資料稀疏;3) 延遲反饋等。

ESMM 模型提出了下述的網路結構進行問題建模:

EMMS 的特點是:
1. 在整個樣本空間建模。pCVR 可以在先估計出 pCTR 和 pCTCVR 之後計算得出,如下述公式。從原理上看,相當於分別單獨訓練兩個模型擬合出 pCTR 和 pCTCVR,進而計算得到 pCVR。

註意到 pCTR 和 pCTCVR 是在整個樣本空間上建模得到的,pCVR 只是一個中間變數。因此,ESMM 模型是在整個樣本空間建模,而不像傳統 CVR 預估模型那樣只在點選樣本空間建模。
2. 特徵表示層共享。ESMM 模型借鑒遷移學習和 multi-task learning 的思路,在兩個子網路的 embedding 層共享特徵表示詞典。embedding 層的表達引數佔了整個網路引數的絕大部分,引數量大,需要大量的訓練樣本才能學習充分。顯然 CTR 任務的訓練樣本量要大大超過 CVR 任務的訓練樣本量,ESMM 模型中特徵表示共享的機制能夠使得 CVR 子任務也能夠從只有展現沒有點選的樣本中學習,從而在一定程度上緩解訓練資料稀疏性問題。
各種模型的對比和總結
前面介紹了各種基於深度學習的廣告點選率預估演演算法模型,針對不同的問題、基於不同的思路,不同的模型有各自的特點。各個模型具體關係比較如下表 1 所示:
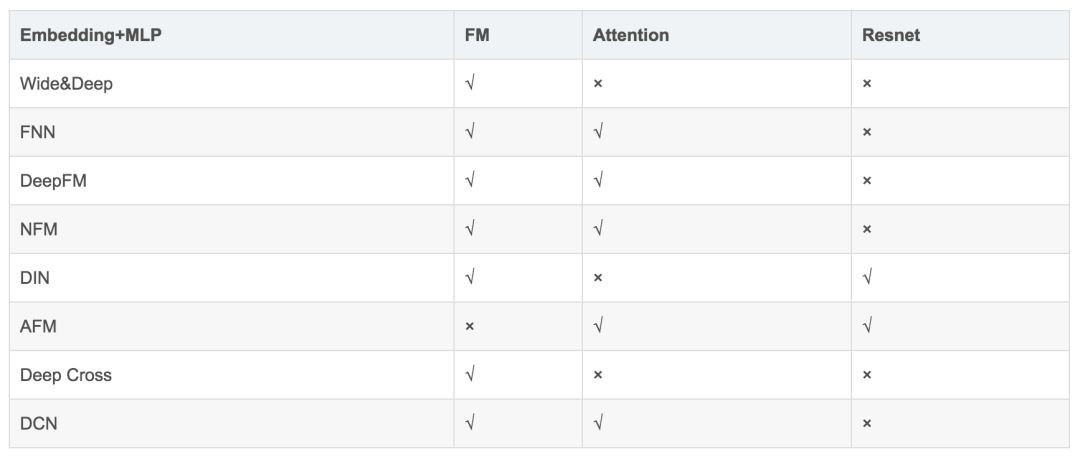
▲ 表1. 各模型對比
本文從開篇就說明這些模型推演的核心思路是“透過設計網路結構進行組合特徵的挖掘”,其在各個模型的實現方式如下:
1. FM 其實是對嵌入特徵進行兩兩內積實現特徵二階組合;FNN 在 FM 基礎上引入了 MLP;
2. DeepFM 透過聯合訓練、嵌入特徵共享來兼顧 FM 部分與 MLP 部分不同的特徵組合機制; 3. NFM、PNN 則是透過改造向量積的方式來延遲FM的實現過程,在其中新增非線性成分來提升模型表現力;
4. AFM 更進一步,直接透過子網路來對嵌入向量的兩兩逐元素乘積進行加權求和,以實現不同組合的差異化,也是一種延遲 FM 實現的方式;
5. DCN 則是將 FM 進行高階特徵組合的方向上進行推廣,並結合 MLP 的全連線式的高階特徵組合機制;
6. Wide&Deep; 是相容手工特徵組合與 MLP 的特徵組合方式,是許多模型的基礎框架;
7. Deep Cross 是引入殘差網路機制的前饋神經網路,給高維的 MLP 特徵組合增加了低維的特徵組合形式,啟發了 DCN;
8. DIN 則是對使用者側的某歷史特徵和廣告側的同領域特徵進行組合,組合成的權重反過來重新影響使用者側的該領域各歷史特徵的求和過程;
9. 多工視角則是更加宏觀的思路,結合不同任務(而不僅是同任務的不同模型)對特徵的組合過程,以提高模型的泛化能力。
當然,廣告點選率預估深度學習模型還有很多,比如 Jie Zhu 提出的基於決策樹的神經網路(Deep Embedding Forest)將深度學習與樹型模型結合起來。如果資料特徵存在影象或者大量文字相關特徵,傳統的摺積神經網路、迴圈神經網路均可以結合到廣告點選率預估的場景中。各個深度模型都有相應的特點,限於篇幅,我們就不再贅述了。
後記
目前深度學習的演演算法層出不窮,看論文確實有些應接不暇。我們的經驗有兩點:要有充分的生產實踐經驗,同時要有扎實的演算法理論基礎。很多論文的亮點其實是來自於實際做工程的經驗。也幸虧筆者一直都在生產一線並帶領演演算法團隊進行工程研發,積澱了一些特徵工程、模型訓練的經驗,才勉強跟得上新論文。比如 DIN“對使用者側的某領域歷史特徵基於廣告側的同領域特徵進行加權求和”的思想,其實與傳統機器學習對強業務相關特徵進行針對性特徵組合的特徵工程思路比較相似。
另一方面,對深度學習的經典、前沿方法的熟悉也很重要。從前面我們的串講也能夠看出,CTR 預估作為一個業務特點很強的場景,在應用深度學習的道路上,也充分借鑒了註意力機制、殘差網路、聯合訓練、多工學習等經典的深度學習方法。瞭解博主的朋友也知道我們一直推崇理論與實踐相結合的思路,我們自身對這條經驗也非常受用。當然,計算廣告是一個很深的領域,自己研究尚淺,串講難免存在紕漏。歡迎大家指出問題,共同交流學習。
參考文獻
1. 陳巧紅,餘仕敏,賈宇波. 廣告點選率預估技術綜述[J]. 浙江理工大學學報. 2015(11).
2. 紀文迪,王曉玲,周傲英. 廣告點選率估算技術綜述[J]. 華東師範大學學報(自然科學版). 2013(03).
3. Rendle S. Factorization machines. Data Mining (ICDM), 2010 IEEE 10th International Conference on. 2010.
4. Heng-Tze Cheng and Levent Koc. Wide & deep learning for recommender systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems, pages 7–10. ACM, 2016.
5. Weinan Zhang, Tianming Du, and Jun Wang. Deep learning over multi-field categorical data – – A case study on user response prediction. In ECIR, 2016.
6. Huifeng Guo, Ruiming Tang, Yunming Ye, Zhenguo Li, and Xiuqiang He. DeepFM: A Factorization-Machine based Neural Network for CTR Prediction. arXiv preprint arXiv:1703.04247 (2017).
7. Xiangnan He and Tat-Seng Chua. Neural Factorization Machines for Sparse Predictive Analytics SIGIR. 355–364. 2017.
8. Guorui Zhou, Chengru Song, Xiaoqiang Zhu, Xiao Ma, Yanghui Yan, Xingya Dai, Han Zhu, Junqi Jin, Han Li, and Kun Gai. 2017. Deep Interest Network for Click-Through Rate Prediction. arXiv preprint arXiv:1706.06978 (2017).
9. J. Xiao, H. Ye, X. He, H. Zhang, F. Wu, and T.-S. Chua. Attentional factorization machines: Learning the weight of feature interactions via attention networks. In IJCAI, 2017.
10. Ying Shan, T Ryan Hoens, Jian Jiao, Haijing Wang, Dong Yu, and JC Mao. 2016. Deep Crossing: Web-Scale Modeling without Manually Cra ed Combinatorial Features. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 255–262.
11. Wang, R., Fu, B., Fu, G., Wang, M.: Deep & cross network for ad click predictions. In: Proceedings of the ADKDD 17. pp. 12:1–12:7 (2017).
12. Ying Shan, T Ryan Hoens, et al. Deep crossing: Web-scale modeling without manually crafted combinatorial features. KDD ’16. ACM, 2016.
13. Paul Covington, Jay Adams, and Emre Sargin. Deep neural networks for youtube recommendations. In Proceedings of the 10th ACM Conference on Recommender Systems, pages 191–198. ACM, 2016.
14. Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2015. Deep residual learning for image recognition. arXiv preprint arXiv:1512.03385 (2015).
關於PaperWeekly
PaperWeekly 是一個推薦、解讀、討論、報道人工智慧前沿論文成果的學術平臺。如果你研究或從事 AI 領域,歡迎在公眾號後臺點選「交流群」,小助手將把你帶入 PaperWeekly 的交流群裡。

▽ 點選 | 閱讀原文 | 加入社群刷論文
 知識星球
知識星球