作者丨蘇劍林

單位丨廣州火焰資訊科技有限公司

研究方向丨NLP，神經網路

個人主頁丨kexue.fm

說到噪聲對比估計，或者“負取樣”，大家可能立馬就想到了 Word2Vec。事實上，它的含義遠不止於此，噪音對比估計（NCE, Noise Contrastive Estimation）是一個迂迴但卻異常精美的技巧，它使得我們在沒法直接完成歸一化因子（也叫配分函式）的計算時，就能夠去估算出機率分佈的引數。本文就讓我們來欣賞一下 NCE 的曲徑通幽般的美妙。

註：由於出發點不同，本文所介紹的“噪聲對比估計”實際上更偏向於所謂的“負取樣”技巧，但兩者本質上是一樣的，在此不作區分。

問題起源

問題的根源是難分難捨的指數機率分佈。

指數族分佈

在很多問題中都會出現指數族分佈，即對於某個變數 x 的機率 p(x)，我們將其寫成：

其中 G(x) 是 x 的某個“能量”函式，而則是歸一化常數，也叫配分函式。這種分佈也稱為“玻爾茲曼分佈”。

在機器學習中，指數族分佈的主要來源有兩個。第一個來源是 softmax：我們做分類預測時，通常最後都會將全連線層的結果用 softmax 啟用，這就是一個離散的、有限個點的玻爾茲曼分佈了；第二個則是來源於最大熵原理：當我們引入某個特徵並且已經能估算出特徵的期望時，最大熵模型告訴我們其分佈應該是特徵的指數形式。

難算的配分函式

總的來說，指數族分佈是非常實用的一類分佈，不論是機器學習、數學還是物理領域，都能夠碰見它。然而，它卻有一個比較大的問題：不容易算，準確來說是配分函式不容易算。

具體來說，不好算的原因可能有兩個。一個是計算量太大，比如語言模型（包括 Word2Vec）的場景，因為要透過背景關係來預測當前詞的分佈情況，這就需要對幾十萬甚至幾百萬項（取決於詞表大小）進行求和來算歸一化因子，這種情況下不是不能算，而是計算量大到難以承受了。

另一種情況是根本算不出來，比如假設，那麼就有：

這積分根本就沒法簡單地算出來呀，更不用說更加複雜的函式了。現在我們也許能從這個角度感受到為什麼高斯分佈那麼常用了，因為，因為，因為，換個分佈就沒法算下去了……

在機器學習中，如果只是分類、預測，那麼歸一化因子算不算出來都無所謂，因為我們只要相對比較取出最大的那個。但是在預測之前，我們還面臨著訓練的問題，也就是引數估計，具體來說，G(x) 其實是含有一些位置引數 θ 的，準確來說要寫成 G(x;θ)，那麼機率分佈就是：

我們要從 x 的樣本中推算出 θ 來，通常我們會用最大似然，但是不算出 Z(θ) 來我們就沒法算似然函式，也就沒法做下去了。

NCE登場

非常幸運的是，NCE 誕生了，它成功地繞開了這個困難。對於配分函式算不出來的情形，它提供了一種算下去的可能性；對於配分函式計算量太大的情形，它還提供了一種降低計算量的方案。

變成二分類問題

NCE 的思想很簡單，它希望我們將真實的樣本和一批“噪聲樣本”進行對比，從中發現真實樣本的規律出來。

具體來說，能量還是原來的能量 G(x;θ)，但這時候我們不直接算機率 p(x) 了，因為歸一化因子很難算。我們去算：

這裡的 θ 還是原來的待最佳化引數，而 γ 則是新引入的要最佳化的引數。

然後，NCE 的損失函式變為：

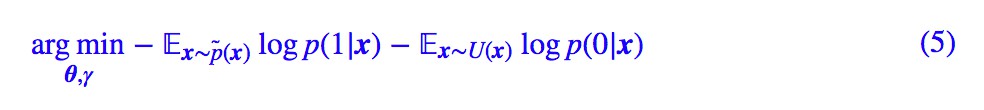
其中 p̃(x) 是真實樣本，U(x) 是某個“均勻”分佈或者其他的、確定的、方便取樣的分佈。

說白了，NCE 的做法就是將它轉化為二分類問題，將真實樣本判為 1，從另一個分佈取樣的樣本判為 0。

等價於原來分佈

現在的問題是，從 (5) 式估算出來的 θ，跟直接從 (3) 式的最大似然估計（理論上是可行的）出來的結果是不是一樣的。

答案是基本一樣的。我們將 (5) 式中的 loss 改寫為：

因為 p̃(x) 和 U(x) 都跟引數 θ，γ 沒關，因此將 loss 改為下麵的形式，不會影響最佳化結果：

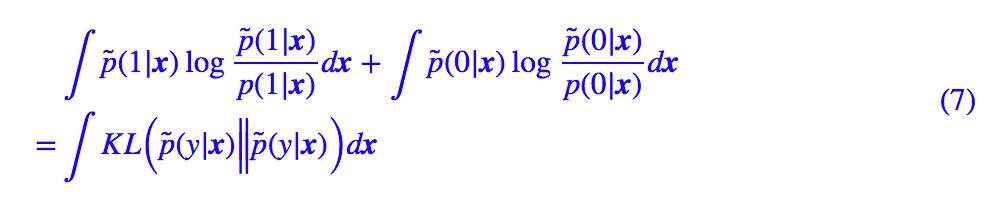
其中：

(7) 式是 KL 散度的積分，而 KL 散度非負，那麼當“假設的分佈形式是滿足的、並且充分最佳化”時，(7) 式應該為 0，從而我們有 p̃(y|x)=p(y|x)，也就是：

從中可以解得：

如果 U(x) 取均勻分佈，那麼 U(x) 就只是一個常數，所以最終的效果表明 γ−logU(x) 起到了 logZ 的作用，而分佈還是原來的分佈 (3)，θ 還是原來的 θ。

這就表明瞭 NCE 就是一種間接最佳化 (3) 式的巧妙方案：看似迂迴，實則結果等價，並且 (5) 式的計算量也大大減少，因為計算量就只取決於取樣的數目了。

一些插曲

一些跟 NCE 相關的話題，就都放在這裡了。

NCE與負取樣簡述

NCE 的系統提出是在 2010 年的論文 Noise-contrastive estimation: A new estimation principle for unnormalized statistical models 中，後面訓練大規模的神經語言模型基本上都採用 NCE 或者類似的 loss 了。

論文的標題其實就表明瞭 NCE 的要點：它是“非歸一化模型”的一個“引數估計原理”，專門應對歸一化因子難算的場景。

但事實上，“負取樣”的思想其實早就被使用了，比如就在 2008 年的 ICML 上，Ronan Collobert 和 Jason Weston 在發表的 A Unified Architecture for Natural Language Processing: Deep Neural Networks with Multitask Learning 中已經用到了負取樣的方法來訓練詞向量。

要知道，那時候距離 Word2Vec 釋出還有四五年。關於詞向量和語言模型的故事，請參考 licstar 的《詞向量和語言模型》[1]。

基於同樣的為了降低計算量的需求，後來Google的Word2Vec也用上了負取樣技巧，在很多工下，它還比基於Huffman Softmax的效果要好，尤其是那個“詞類比（word analogy）”實驗。這裡邊的奧妙，我們馬上就來分析。

Word2Vec

現在我們落實到 Word2Vec 來分析一些事情。以 Skip Gram 模型為例，Word2Vec 的標的是：

其中 ui，vj 都是待最佳化引數，代表著背景關係和中心詞的兩套不同的詞向量空間。顯然地，這裡的問題就是歸一化因子計算量大，其中應對方案有 Huffman Softmax 和負取樣。

這裡我們不關心 Huffman Softmax，只需要知道它就是原來標準 Softmax 的一種近似就行了。我們來看負取樣的，Word2Vec 將最佳化標的變為了：

這個式子看著有點眼花，總之它就是表達了“語料出現的 Skip Gram 視為正樣本，隨機取樣的詞作為負樣本”的意思。

首先最明顯的是，(12) 式相比 (4)，(5) 式，少引入了 γ 這個訓練引數，或者就是說預設了 γ=0，這允許嗎？據說確實有人做過對比實驗，結果顯示訓練出來的 γ 確實在 0 上下浮動，因此這個預設操作基本上是合理的。

其次，對於負樣本，Word2Vec 可不是“均勻地取樣每一個詞”，而是按照每個詞本身的總詞頻來取樣的。這樣一來，(10) 式就變成了：

也就是說，最終的擬合效果是：

大家可以看到，左邊就是兩個詞的互資訊。本來我們的擬合標的是兩個詞的內積等於條件機率 p̃(wj|wi)（的對數），現在經過負取樣的 Word2Vec，兩個詞的內積就是兩個詞的互資訊。

現在大概就可以解釋為什麼 Word2Vec 的負取樣會比 Huffman Softmax 效果要好些了。Huffman Softmax 只是對 Softmax 做了近似，它本質上還是在擬合 p̃(wj|wi)，而負取樣技巧則是在擬合互資訊。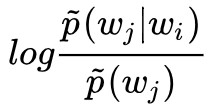

我們之後，Word2Vec 是靠詞的共現來反應詞義的，互資訊比條件機率 p̃(wj|wi)更能反映詞與詞之間“真正的”共現關係。換言之，p̃(wj|wi) 反映的可能是“我認識周傑倫，周傑倫卻不認識我”的關係，而互資訊反映的是“你認識我，我也認識你”的關係，後者更能體現出語意關係。

我之前構造的另一個詞向量模型《更別緻的詞向量模型（三）：描述相關的模型》[2] 中也表明瞭，基於互資訊出發構造的模型，能理論上解釋“詞類比（word analogy）”等很多實驗結果，這也間接證實了，基於互資訊的“Skip Gram + 負取樣”組合，是 Word2Vec 的一個絕佳組合。

所以，根本原因不是 Huffman Softmax 和負取樣本身誰更優的問題，而是它們的最佳化標的就已經不同。

列車已到終點站

本文的目的是介紹 NCE 這種精緻的引數估算技巧，指出它可以在難以為完成歸一化時來估算機率分佈中的引數，原則上這是一種通用的方法，而且很可能，在某些場景下它是唯一可能的方案。

最後我們以 Word2Vec 為具體例子進行簡單的分析，談及了使用 NCE 時的一些細節問題，並且順帶解釋了負取樣為什麼好的這個問題。

“噪聲對比估計”雜談：曲徑通幽之妙

問題起源

NCE登場

一些插曲

列車已到終點站

相關連結

相關推薦

熱門標籤

熱門文章

分享創造快樂