手把手教你在多種無監督聚類演演算法實現Python（附程式碼）-知識星球

來源：機器之心

本文約2704字，建議閱讀6分鐘。

本文簡要介紹了多種無監督學習演演算法的 Python 實現，包括 K 均值聚類、層次聚類、t-SNE 聚類、DBSCAN 聚類。

無監督學習是一類用於在資料中尋找樣式的機器學習技術。無監督學習演演算法使用的輸入資料都是沒有標註過的，這意味著資料只給出了輸入變數（自變數 X）而沒有給出相應的輸出變數（因變數）。在無監督學習中，演演算法本身將發掘資料中有趣的結構。

人工智慧研究的領軍人物 Yan Lecun，解釋道：無監督學習能夠自己進行學習，而不需要被顯式地告知他們所做的一切是否正確。這是實現真正的人工智慧的關鍵！

監督學習 VS 無監督學習

在監督學習中，系統試圖從之前給出的示例中學習。（而在無監督學習中，系統試圖從給定的示例中直接找到樣式。）因此，如果資料集被標註過了，這就是一個監督學習問題；而如果資料沒有被標註過，這就是一個無監督學習問題。

上圖是一個監督學習的例子，它使用回歸技術找到在各個特徵之間的最佳擬合曲線。而在無監督學習中，根據特徵對輸入資料進行劃分，並且根據資料所屬的簇進行預測。

重要的術語

特徵：進行預測時使用的輸入變數。
預測值：給定一個輸入示例時的模型輸出。
示例：資料集中的一行。一個示例包含一個或多個特徵，可能還有一個標簽。
標簽：特徵對應的真實結果（與預測相對應）。

準備無監督學習所需的資料

在本文中，我們使用 Iris 資料集來完成初級的預測工作。這個資料集包含 150 條記錄，每條記錄由 5 個特徵構成——花瓣長度、花瓣寬度、萼片長度、萼片寬度、花的類別。花的類別包含 Iris Setosa、Iris VIrginica 和 Iris Versicolor 三種。本文中向無監督演演算法提供了鳶尾花的四個特徵，預測它屬於哪個類別。

本文使用 Python 環境下的 sklearn 庫來載入 Iris 資料集，並且使用 matplotlib 進行資料視覺化。以下是用於探索資料集的程式碼片段：

# Importing Modules
from sklearn import datasets
import matplotlib.pyplot as plt

# Loading dataset
iris_df = datasets.load_iris()

# Available methods on dataset
print(dir(iris_df))

# Features
print(iris_df.feature_names)

# Targets
print(iris_df.target)

# Target Names
print(iris_df.target_names)
label = {0: ‘red’, 1: ‘blue’, 2: ‘green’}

# Dataset Slicingx_axis = iris_df.data[:, 0] # Sepal Length
y_axis = iris_df.data[:, 2] # Sepal Width

# Plotting
plt.scatter(x_axis, y_axis, c=iris_df.target)
plt.show()

紫色：Setosa，綠色：Versicolor，黃色：Virginica

聚類分析

在聚類分析中，資料被劃分為不同的幾組。簡而言之，這一步旨在將具有相似特徵的群組從整體資料中分離出來，並將它們分配到簇（cluster）中。

視覺化示例：

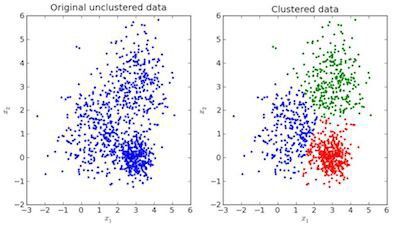
如上所示，左圖是沒有進行分類的原始資料，右圖是進行聚類之後的資料（根據資料本身的特徵將其分類）。當給出一個待預測的輸入時，它會基於其特徵檢視自己從屬於哪一個簇，並以此為根據進行預測。

K-均值聚類的 Python 實現

K 均值是一種迭代的聚類演演算法，它的標的是在每次迭代中找到區域性最大值。該演演算法要求在最初選定聚類簇的個數。由於我們知道本問題涉及到 3 種花的類別，所以我們透過將引數「n_clusters」傳遞給 K 均值模型來編寫演演算法，將資料分組到 3 個類別中。現在，我們隨機地將三個資料點（輸入）分到三個簇中。基於每個點之間的質心距離，下一個給定的輸入資料點將被劃分到獨立的簇中。接著，我們將重新計算所有簇的質心。

每一個簇的質心是定義結果集的特徵值的集合。研究質心的特徵權重可用於定性地解釋每個簇代表哪種型別的群組。

我們從 sklearn 庫中匯入 K 均值模型，擬合特徵併進行預測。

K 均值演演算法的 Python 實現：

# Importing Modules
from sklearn import datasets
from sklearn.cluster import KMeans

# Loading dataset
iris_df = datasets.load_iris()
# Declaring Model
model = KMeans(n_clusters=3)

# Fitting Model
model.fit(iris_df.data)# Predicitng a single input
predicted_label = model.predict([[7.2, 3.5, 0.8, 1.6]])

# Prediction on the entire data
all_predictions = model.predict(iris_df.data)

# Printing Predictions
print(predicted_label)
print(all_predictions)

層次聚類

層次聚類，顧名思義，是一種能夠構建有層次的簇的演演算法。在這個演演算法的起始階段，每個資料點都是一個簇。接著，兩個最接近的簇合二為一。最終，當所有的點都被合併到一個簇中時，演演算法停止。

層次聚類的實現可以用 dendrogram 進行展示。接下來，我們一起來看一個糧食資料的層次聚類示例。

資料集連結：https://raw.githubusercontent.com/vihar/unsupervised-learning-with-python/master/seeds-less-rows.csv

層次聚類的 Python 實現：

# Importing Modules
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
import pandas as pd

# Reading the DataFrame
seeds_df = pd.read_csv(
 "https://raw.githubusercontent.com/vihar/unsupervised-learning-with-python/master/seeds-less-rows.csv")

# Remove the grain species from the DataFrame, save for later
varieties = list(seeds_df.pop('grain_variety'))

# Extract the measurements as a NumPy array
samples = seeds_df.values

"""
Perform hierarchical clustering on samples using the
linkage() function with the method='complete' keyword argument.
Assign the result to mergings.
"""mergings = linkage(samples, method='complete')

"""
Plot a dendrogram using the dendrogram() function on mergings,
specifying the keyword arguments labels=varieties, leaf_rotation=90,
and leaf_font_size=6.
"""
dendrogram(mergings,
 labels=varieties,
 leaf_rotation=90,
 leaf_font_size=6,
 )

plt.show()

K 均值和層次聚類之間的差別

層次聚類不能很好地處理大資料，而 K 均值聚類可以。原因在於 K 均值演演算法的時間複雜度是線性的，即 O(n)；而層次聚類的時間複雜度是平方級的，即 O(n2)。
在 K 均值聚類中，由於我們最初隨機地選擇簇，多次執行演演算法得到的結果可能會有較大差異。而層次聚類的結果是可以復現的。
研究表明，當簇的形狀為超球面（例如：二維空間中的圓、三維空間中的球）時，K 均值演演算法效能良好。
K 均值演演算法抗噪聲資料的能力很差（對噪聲資料魯棒性較差），而層次聚類可直接使用噪聲資料進行聚類分析。

t-SNE 聚類

這是一種視覺化的無監督學習方法。t-SNE 指的是 t 分佈隨機鄰居嵌入（t-distributed stochastic neighbor embedding）。它將高維空間對映到一個視覺化的二維或三維空間中。具體而言，它將透過如下方式用二維或三維的資料點對高維空間的物件進行建模：以高機率用鄰近的點對相似的物件進行建模，而用相距較遠的點對不相似的物件進行建模。

用於 Iris 資料集的 t-SNE 聚類的 Python 實現：

# Importing Modules
from sklearn import datasets
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt

# Loading dataset
iris_df = datasets.load_iris()

# Defining Model
model = TSNE(learning_rate=100)

# Fitting Model
transformed = model.fit_transform(iris_df.data)# Plotting 2d t-Sne
x_axis = transformed[:, 0]
y_axis = transformed[:, 1]

plt.scatter(x_axis, y_axis, c=iris_df.target)
plt.show()

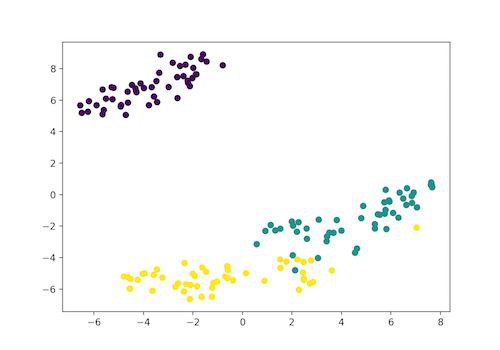
紫色：Setosa，綠色：Versicolor，黃色：Virginica

在這裡，具備 4 個特徵（4 維）的 Iris 資料集被轉化到二維空間，並且在二維影象中進行展示。類似地，t-SNE 模型可用於具備 n 個特徵的資料集。

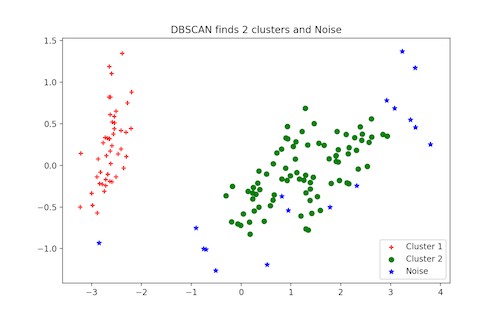
DBSCAN 聚類

DBSCAN（帶噪聲的基於密度的空間聚類方法）是一種流行的聚類演演算法，它被用來在預測分析中替代 K 均值演演算法。它並不要求輸入簇的個數才能執行。但是，你需要對其他兩個引數進行調優。

scikit-learn 的 DBSCAN 演演算法實現提供了預設的“eps”和“min_samples”引數，但是在一般情況下，使用者需要對他們進行調優。引數“eps”是兩個資料點被認為在同一個近鄰中的最大距離。引數“min_samples”是一個近鄰中在同一個簇中的資料點的最小個數。

DBSCAN 聚類的 Python 實現：

# Importing Modules
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.decomposition import PCA

# Load Dataset
iris = load_iris()

# Declaring Model
dbscan = DBSCAN()
# Fitting
dbscan.fit(iris.data)

# Transoring Using PCA
pca = PCA(n_components=2).fit(iris.data)
pca_2d = pca.transform(iris.data)

# Plot based on Class
for i in range(0, pca_2d.shape[0]):
if dbscan.labels_[i] == 0:
c1 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c=’r’, marker=’+’)
elif dbscan.labels_[i] == 1:c2 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c=’g’, marker=’o’)
elif dbscan.labels_[i] == -1:
c3 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c=’b’, marker=’*’)

plt.legend([c1, c2, c3], [‘Cluster 1’, ‘Cluster 2’, ‘Noise’])
plt.title(‘DBSCAN finds 2 clusters and Noise’)
plt.show()