
導讀: 直觀來看,處理大資料的一個方法就是減少要處理的資料量,從而使處理的資料量能夠達到當前的處理能力能夠處理的程度。可以使用的方法主要包括抽樣和過濾。兩者的區別是,抽樣主要依賴隨機化技術,從資料中隨機選出一部分樣本,而過濾依據限制條件僅選擇符合要求的資料參與下一步驟的計算。

01 資料抽樣
一般來說,設一個總體含有N個個體,從中逐個不放回地抽取n個個體作為樣本(n≤N),如果每次抽取使總體內的各個個體被抽到的機會都相等,就把這種抽樣方法叫作簡單隨機抽樣。從抽樣的隨機性上來看抽樣可以分為隨機抽樣、分層抽樣、整群抽樣和系統抽樣,下麵依次對這些方法進行介紹。
爭論:大資料與抽樣
在《大資料時代》一書中提到,大資料的方法被定義為“採用全量資料而不用抽樣的方法”,因而,有人認為大資料和抽樣是矛盾的,抽樣技術不能應用到大資料分析上。然而,在資料量大到一定規模的時候,不用抽樣、而採用全部資料的方法將無法使用。例如,某個公司要對客戶進行分類。如果採用客服回訪的方式來進行分類的話,要求全量回訪,一個月有幾百萬的使用者,根本不可能做完。但如果是抽樣,加上相關指標去訓練模型,就能快速高效的解決。
而且,由於大資料價值密度低,很多場景下,僅選擇一小部分資料就能夠窺到資料全貌。特別採用一些隨機化演演算法設計與分析分析技術的情況下,可以證明,即使採用抽樣的方法,甚至在樣本個數與資料量無關的時候,計算結果的精度同樣是有所保證的。
1. 隨機抽樣
隨機抽樣 (也成為抽簽法、隨機樣數表法)常常用於總體個數較少時,它的主要特徵是從總體中逐個抽取。其優點是操作簡便易行,缺點是在樣本總體過大不易實行。
主要方法包括:
(1)抽簽法
一般地,抽簽法就是把總體中的N個個體編號,把號碼寫在號簽上,將號簽放在一個容器中,攪拌均勻後,每次從中抽取一個號簽,連續抽取n次,就得到一個容量為n的樣本。
比如,某高中要調查高一學生平均每天學習英語的時間資訊,假設一個年級有1000人,從中抽取100名進行調查,整個過程可以看成,我們將1000人從1到1000進行編號,並給予相應的號簽。然後將1000個號簽攪拌均勻,並隨機從中取出100個號簽,再對號碼一致的學生進行調查。
這種方法簡單易行,適用於總體中的個數不多時。當總體中的個體數較多時,將總體“攪拌均勻”就比較困難,用抽簽法產生的樣本代表性差的可能性很大。
(2)隨機數法
隨機抽樣中,另一個經常被採用的方法是隨機數法,即利用隨機數表、隨機數骰子或計算機產生的隨機數進行抽樣。
例如C語言中提供的rand()函式可以用來產生隨機數,但是這不是真正意義上的隨機數,是一個偽隨機數,是根據一個數(我們可以稱它為種子)為基準以某個遞推公式推算出來的一系列數,當這系列數很大的時候,就符合正態公佈,從而相當於產生了隨機數,但這不是真正的隨機數。比如寫一條C++陳述句:cout<
(3)水庫抽樣
現在需要我們在有限的儲存空間裡解決無限的資料(含有海量資料的資料流)等機率抽樣的問題。
我們首先從最簡單的例子出發:要求我們在任意時刻只能儲存一個資料,但要保證等機率的抽樣。
假設資料流只有一個資料。我們接收資料,發現資料流結束了,直接傳回該資料,該資料傳回的機率為1。
再假設資料流裡有兩個資料,我們讀到了第一個資料,這次我們不能直接傳回該資料,因為資料流沒有結束。我們繼續讀取第二個資料,發現資料流結束了。因此我們只要保證以相同的機率傳回第一個或者第二個資料就可以滿足要求。因此我們生成一個0到1的隨機數R, 如果R小於0.5我們就傳回第一個資料,如果R大於0.5,傳回第二個資料。
接著我們繼續分析有三個資料的資料流的情況。為了方便,我們按順序給流中的資料命名為1、2、3。我們陸續收到了資料1、2。和前面的例子一樣,我們只能儲存一個資料,所以必須淘汰1和2中的一個。應該如何淘汰呢?不妨和上面例子一樣,我們按照二分之一的機率淘汰一個,例如我們淘汰了2。
繼續讀取流中的資料3,發現資料流結束了,我們知道在長度為3的資料流中,如果傳回資料3的機率為1/3, 那麼才有可能保證選擇的正確性。也就是說,目前我們手裡有1,3兩個資料,我們透過一次隨機選擇,以1/3的機率留下資料3,以2/3的機率留下資料1。那麼資料1被最終留下的機率是多少呢?經過分析有:
-
資料1被留下:(1/2)*(2/3) = 1/3
-
資料2被留下機率:(1/2)*(2/3) = 1/3
-
資料3被留下機率:1/3
我們做一下推論:假設當前正要讀取第n個資料,則我們以1/n的機率留下該資料,否則留下前n-1個資料中的一個。以這種方法選擇,所有資料流中資料被選擇的機率一樣。
下麵給出簡單的證明:
假設n-1時候成立,即前n-1個資料被傳回的機率都是1/n-1,當前正在讀取第n個資料,以1/n的機率傳回它。那麼前n-1個資料中資料被傳回的機率為:(1/(n-1))*((n-1)/n)= 1/n,假設成立。

2. 系統抽樣
當總體中的個體數較多時,採用簡單隨機抽樣效率低下。這時,可將總體分成均衡的幾個部分,然後按照預先定出的規則,從每一部分抽取一個個體,得到所需要的樣本,這種抽樣叫作系統抽樣。假設要從容量為N的總體中抽取容量為n的樣本,可以按下列步驟進行系統抽樣:
-
先將總體的N個個體編號。有時可直接利用個體自身所帶的號碼進行編號,如學號、準考證號、門牌號等;
-
確定分段間隔k,對編號進行分段。當N/n(n是樣本容量)是整數時,取k=N/n;
-
在第一段用簡單隨機抽樣確定第一個個體編號l(l≤k);
-
按照一定的規則抽取樣本。通常是將l加上間隔k得到第2個個體編號(l+k),再加k得到第3個個體編號(l+2k),依次進行下去,直到獲取整個樣本。
例如, 為瞭解某大學一年級新生英語學習的情況,擬從503名大學一年級學生中抽取50名作為樣本,目的是採用系統抽樣方法完成這一抽樣。
由於總樣本的個數為503,抽樣樣本的容量為50,不能整除,可採用隨機抽樣的方法從總體中剔除3個個體,使剩下的個體數500能被樣本容量50整除,然後再採用系統抽樣方法。具體步驟如下:
-
第一步,將503名學生用隨機方式編號為1,2,3,…,503;
-
第二步,用抽簽法或隨機數表法,剔除3個個體,這樣剩下500名學生,對剩下的500名學生重新編號,或採用補齊號碼的方式;
-
第三步,確定分段間隔k,將總體分為50個部分,每一部分包括10個個體,這時,每1部分的個體編號為1,2,…,10;第2部分的個體編號為11,12,…,20;依此類推,第50部分的個體編號為491,492,…,500;
-
第四步,在第1部分用簡單隨機抽樣確定起始的個體編號,例如是5;
-
第五步,依次在第2部分,第3部分,…,第50部分,取出號碼為15,25,…,495這樣得到一個容量為50的樣本。
3. 分層抽樣
分層抽樣的主要特徵是分層按比例抽樣,主要使用於總體中的個體有明顯差異。其和隨機抽樣的共同點是每個個體被抽到的機率都相等N/M。
一般地,在抽樣時,將總體分成互不交叉的層,然後按照一定的比例,從各層獨立地抽取一定數量的個體,將各層取出的個體合在一起作為樣本,則這種抽樣方法是一種分層抽樣。我們用一個例子來展示分層抽樣。
例如,一個公司的職工有500人,其中不到30歲有125人,30歲至40歲的有280人,40歲以上的有95人。為了瞭解這個單位職工與身體狀況有關的某項指標,要從中抽取一個容量為100的樣本,由於職工年齡與這項指標有關,故採用分層抽樣方法進行抽取。因為樣本容量與總體的個數的比為1:5,所以在各年齡段抽取的個數依次為125/5,280/5,95/5,即25,56,19。
4. 加權抽樣
首先來解釋加權:加權是透過對總體中的各個樣本設定不同的數值繫數(即權重),使樣本呈現希望的相對重要性程度。
那麼在抽樣時為什麼要加權呢?例如,在城市和農村各調查300樣本,城市人口與農村人口比例“城市:農村=1:2”(假設),在分析時我們希望將城市和農村看作一個整體,這時候我們就可以賦予農村樣本一個2倍於城市樣本的權重;
可以看出,加權抽樣能夠深刻的影響資料分析。
加權方法主要有:
因子加權:對滿足特定變數或指標的所有樣本賦予一個權重,通常用於提高樣本中具有某種特性的被訪者的重要性;例如,研究一種啤酒的口味是否需要改變,那麼不同程度購買者的觀點也應該有不同的重要性對待:例如:經常購買該啤酒的客戶的權重=3,偶爾購買該啤酒的客戶的權重為1,從不購買的客戶的權重為0.1。
標的加權:對某一特定樣本組賦權,以達到們預期的特定標的;例如:我們想要:品牌A的20%使用者 = 品牌B的80%使用者;或者品牌A的80%使用者 = 使用品牌A的20%非使用者。
輪廓加權:多因素加權,標的加權不同(一維的),輪廓加權應用於對調查樣本相互關係不明確的多個屬性加權;面對多個需要賦權的屬性,輪廓加權過程應該同時進行,以盡可能少的對變數產生扭曲。

5. 整群抽樣
整群抽樣又稱聚類抽樣。是將總體中各單位歸併成若干個互不交叉、互不重覆的集合,稱之為群,然後以群為抽樣單位抽取樣本的一種抽樣方式。應用整群抽樣時,要求各群有較好的代表性,即群內各單位的差異要大,群間差異要小。
整群抽樣的優點是實施方便、節省經費;整群抽樣的缺點是往往由於不同群之間的差異較大,由此而引起的抽樣誤差往往大於簡單隨機抽樣。
整群抽樣先將總體分為i個群,然後從i個群鐘隨即抽取若干個群,對這些群內所有個體或單元均進行調查。抽樣過程可分為以下幾個步驟:
-
確定分群的標註;
-
將總體(N)分成若干個互不重疊的部分,每個部分為一群;
-
根據各群樣本量,確定應該抽取的群數;
-
用簡單隨機抽樣或系統抽樣方法,從i群中抽取確定的群數。
例如,調查中學生患近視眼的情況,抽某一個班做統計,進行產品檢驗,每隔8個小時抽1個小時生產的全部產品進行檢驗等。
整群抽樣與分層抽樣在形式上有相似之處,但實際上差別很大。分層抽樣要求各層之間的差異很大,層內個體或單元差異小,而整群抽樣要求群與群之間的差異比較小,群內個體或單元差異大;分層抽樣的樣本是從每個層內抽取若干單元或個體構成,而整群抽樣則是要麼整群抽取,要麼整群不被抽取。
02 資料過濾
在大資料處理之前,除了採用抽樣的方法減小資料量而外,有時候還需要選擇滿足某種條件的資料,從而使得分析集中在具有某種條件的資料上。
例如,在電子商城圖書的銷售表中對“小說”類別的圖書的銷量進行分析,就可以在整個銷售表中選擇出類別為“小說”的圖書。
在大資料處理過程中,資料過濾可以採用資料庫的基本操作來實現,將過濾條件轉換為選擇操作來實現。例如,在SQL語言中,我們可以使用select from where陳述句很容易的實現過濾。
03 基於阿裡雲的抽樣和過濾實現
在阿裡雲中,提供了多種抽樣和過濾的選擇。我們用下麵這個例子來說明抽樣和過濾的使用方法。
《權力的遊戲》是一部中世紀史詩奇幻題材的美國電視連續劇。我們收集了一些關於戰鬥場景的資料,並希望按照特定的條件對資料進行過濾,然後按一定的資料比例,對原始資料進行抽樣。原始資料前10條見下表:
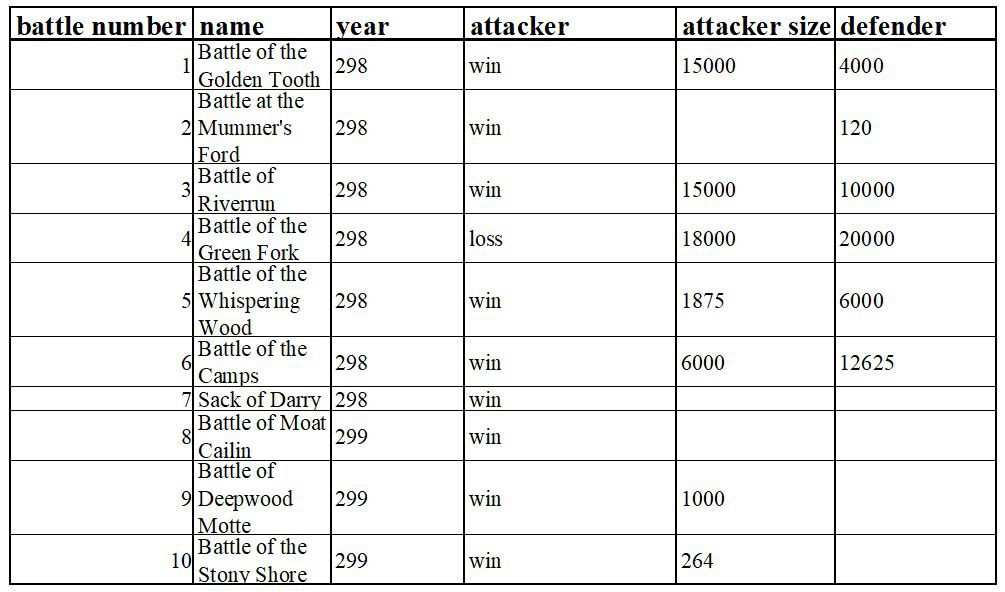
▲關於戰鬥場景的資料
用阿裡雲先進行過濾,然後再分別進行加權抽樣、分層抽樣和隨機抽樣。首先進入阿裡雲大資料開發平臺機器學習平臺,選擇相應的工作組後進入演演算法平臺。在左側實驗中右鍵新建空白實驗,輸入對應的實驗名稱:
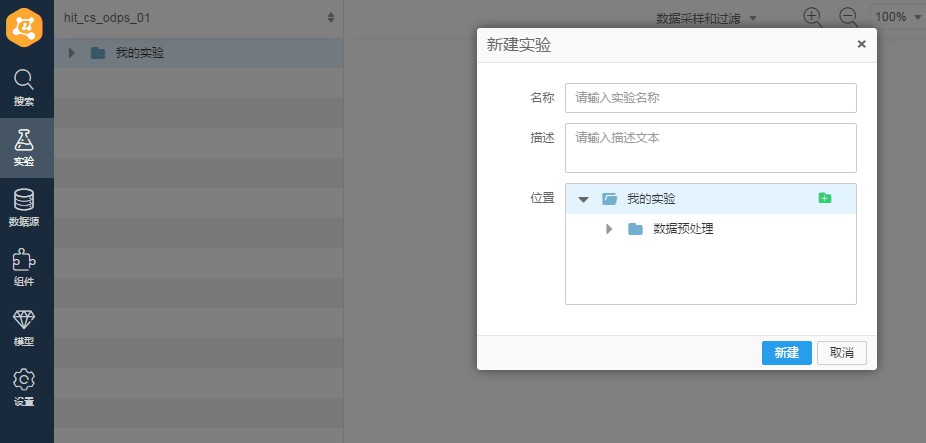
▲新建空白實驗
在元件中選擇相應的元件,拖拽到右側實驗中:
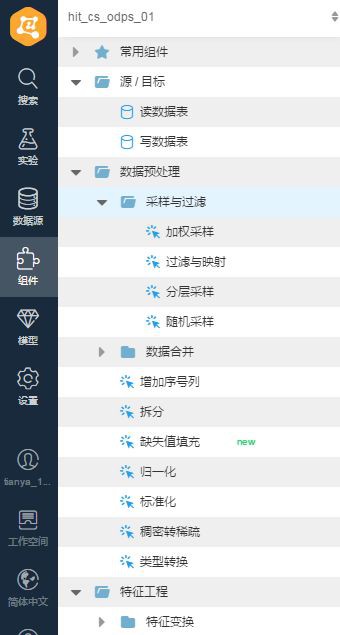
▲選擇相應元件
先對資料進行過濾,然後進行抽樣,最終節點設計如下:
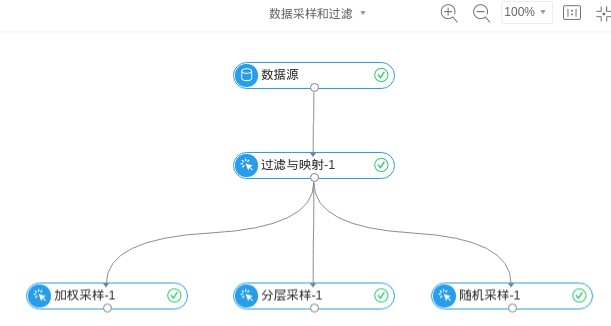
▲程式流圖
過濾引數中,對映規則全選,過濾條件設定為:attacker_outcome = ‘win’,引數設定如下:
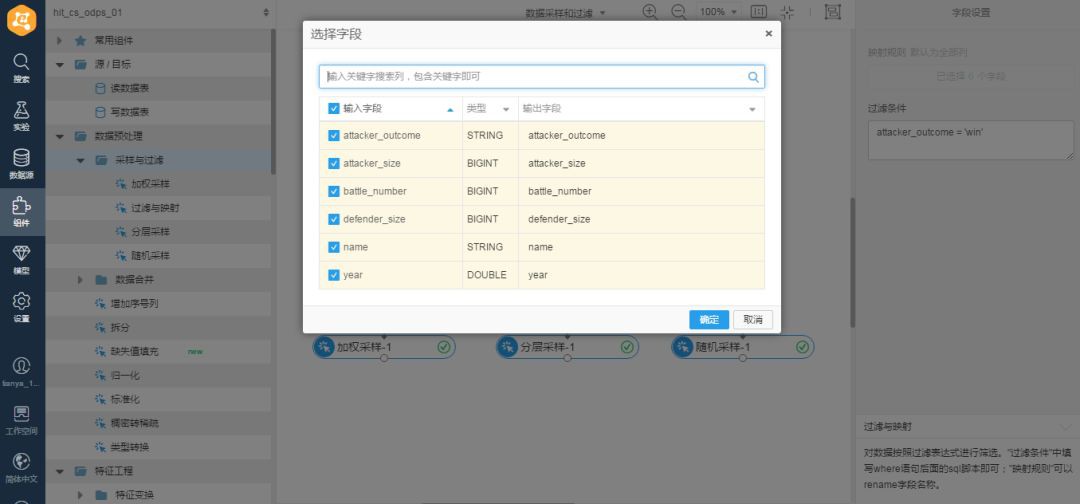
▲引數設定
抽樣引數分別設定如下:

▲加權取樣引數設定

▲分層取樣欄位設定
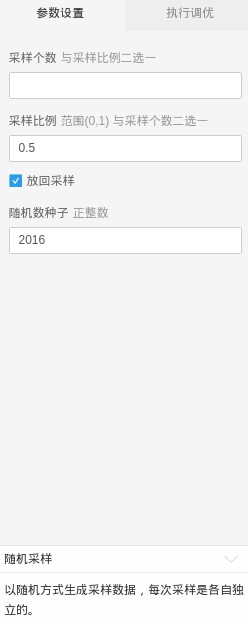
▲隨機取樣引數設定

▲分層取樣引數設定
點選執行,阿裡雲平臺開始執行各實驗節點。完成後,執行成功節點會出現綠色對勾標誌。失敗節點會顯示紅叉標誌。在執行成功節點上點選右鍵,選擇檢視資料,能夠檢視執行結果資料:

▲程式流程
過濾結果如下:

▲過濾結果
抽樣結果分別如下:
加權抽樣如圖:

▲加權抽樣結果
分層抽樣如圖:

▲分層抽樣結果
隨機抽樣如圖:

▲隨機抽樣結果
從抽樣結果看出,加權抽樣依賴權重列數值的權重大小進行抽樣;分層抽樣根據分組列,先對資料進行分組,然後在每個組中進行抽樣;隨機抽樣就是按照抽樣比例,對資料進行抽樣。三種抽樣方式最後得到的結果資料是幾乎完全不同的。
關於作者:王宏志,博士,博士生導師,哈爾濱工業大學電腦科學與技術學院副教授,中國計算機學會高階會員,YOCSEF黑龍江省分論壇AC。研究方向包括XML資料管理、圖資料管理、資料質量、資訊整合等。
本文摘編自《大資料分析原理與實踐》,經出版方授權釋出。
延伸閱讀《大資料分析原理與實踐》
轉載請聯絡微信:togo-maruko
點選文末右下角“寫留言”發表你的觀點
推薦閱讀
Q: 關於抽樣和過濾,你搞懂了嗎?
歡迎留言與大家分享
覺得不錯,請把這篇文章分享給你的朋友
轉載 / 投稿請聯絡:baiyu@hzbook.com
更多精彩,請在後臺點選“歷史文章”檢視

 點選閱讀原文,瞭解更多
點選閱讀原文,瞭解更多
 知識星球
知識星球