
導讀: “三角形內角和等於180°”,這對於我們來說是再熟悉不過的一個常識,陳省身教授從一個不同的角度去看待這個問題,並將這個問題延伸推廣,於1944年,找到了一般曲面上封閉曲線方向改變數總和的公式(高斯—比內—陳公式),把幾何學引入了新的天地,被譽為劃時代的貢獻。
美籍華人陳省身教授是當代舉世聞名的數學家,他十分關心祖國數學科學的發展。人們稱贊他是“中國青年數學學子的總教練”。

▲陳省身教授
1980年,陳教授在北京大學的一次講學中語驚四座:
“人們常說,三角形內角和等於180°。但是,這是不對的!”
大家愕然。怎麼回事?三角形內角和是180°,這不是數學常識嗎?
接著,這位老教授對大家的疑問作了精闢的解答:
說“三角形內角和為180°”不對,不是說這個事實不對,而是說這種看問題的方法不對,應當 說“三角形外角和是360°”!
把眼光盯住內角,只能看到:
三角形內角和是180°;
四邊形內角和是360°;
五邊形內角和是 540°;
…………
n邊形內角和是(n-2)×180°。
這就找到了一個計算內角和的公式。公式裡出現了邊數n。
如果看外角呢?
三角形的外角和是360°;
四邊形的外角和是360°;五邊形的外角和是360°;
…………
任意n邊形外角和都是360°。
這就把多種情形用一個十分簡單的結論概況起來了。用一個與n無關的常數代替了與n有關的公式,找到了更一般的規律。
設想一隻螞蟻在多邊形的邊界上繞圈子(圖1)。每經過一個頂點,它前進的方向就要改變一次,改變的角度恰好是這個頂點處的外角。爬了一圈,回到原處,方向和出發時一致了,角度改變數之和當然恰好是360°。
 圖1
圖1
這樣看問題,不但給“多邊形外角和等於 360°”這條普遍規律找得到了直觀上的解釋,而且立刻把我們的眼光引向了更寬廣的天地。
一條凸的閉曲線——卵形線,談不上什麼內角和與外角和。可是螞蟻在上面爬的時候,它的方向也在時時改變。它爬一圈,角度改變數之和仍是360°(圖2)。
 圖2
圖2
“外角和為360°”,這條規律適用於封閉曲線!不過,敘述起來,要用“方向改變數之和”來代替“外角和”罷了。
對於凹多邊形,就要把“方向改變數總和”改為“方向改變數的代數和”(圖3)。不妨約定:逆時針旋轉的角為正角,順時針旋轉的角為負角。當螞蟻在圖示的凹四邊形的邊界上爬行的時候,在A₁,A₂,A₄處,由方向的改變所成的角是正角:∠1,∠2,∠4;而在A₃處,由方向的改變所成的角是負角:∠3。如果你細細計算一下,這4個角正負相抵,代數和恰是360°。
 圖3
圖3
上面說的都是平面上的情形,曲面上的情形又是怎麼樣呢?地球是圓的。如果你沿著赤道一直向前走,可以繞地球一圈回到原地。但在地面上測量你前進的方向,卻是任何時刻都沒有變化。也就是說:你繞赤道一週,方向改變數總和是0°!
圈子小一點,你在房間裡走一圈,方向改變數看來仍是360°。
不大不小的圈子又怎麼樣呢?如果讓螞蟻沿著地球儀上的北迴歸線繞一圈,它自己感到的(也就是在地球儀錶面上測量到的)方向的改變數應當是多少呢?
用一個圓錐面罩著北極,使圓錐面與地球儀錶面相切的點的軌跡恰好是北迴歸線(圖4)。這樣,螞蟻在球面上的方向的改變數和在錐面上方向的改變數是一樣的。把錐面展開成扇形,便可以看出,螞蟻繞一圈,方向改變數的總和,正好等於這個扇形的圓心角(圖5):
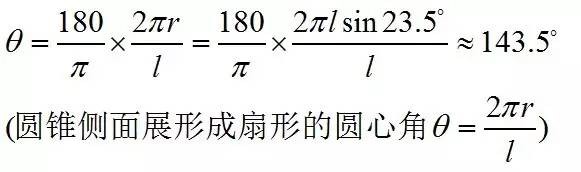

圖4

圖5
要弄清楚這裡面的奧妙,不妨看看螞蟻在金字塔上沿正方形爬一週的情形(圖6)。

圖6
它的方向在拐角處改變了多大角度?把金字塔錶面攤平了一看便知:在B處改變數是180°-(∠1+∠2);繞一圈,改變數是
4×180°-(∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8)
=∠AOB+∠BOC+∠COD+∠DOA
這個和,正是錐面展形後的“扇形角”(圖7)!
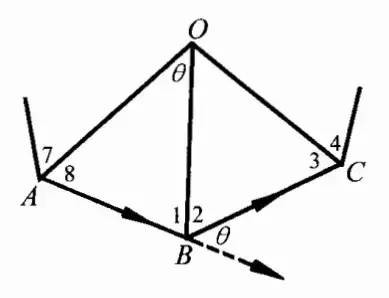 圖7
圖7
早在2000多年前,歐幾裡德時代,人們就已經知道三角形內角和是180°。到了19世紀,德國數學家、被稱為“數學之王”的高斯,在對大地測量的研究中,找到了球面上由大圓弧構成的三角形內角和的公式。又經過幾代數學家的努力,直到1944年,陳省身教授找到了一般曲面上封閉曲線方向改變數總和的公式(高斯—比內—陳公式),把幾何學引入了新的天地。由此發展出來的“陳氏類”理論,被譽為劃時代的貢獻, 在理論物理學上有重要的應用。
從普通的、眾所周知的事實出發,步步深入、推廣,挖掘出廣泛適用的深刻規律。從這裡顯示出數學家透徹、犀利的目光,也表現了數學家窮追不捨、孜孜以求的探索真理的精神。
作者:張景中
來源:數學家的眼光
推薦閱讀
Q: 內角和外角和,你繞明白了嗎?
歡迎留言與大家分享
覺得不錯,請把這篇文章分享給你的朋友
轉載 / 投稿請聯絡:baiyu@hzbook.com
更多精彩,請在後臺點選“歷史文章”檢視

 知識星球
知識星球