
導讀:數量龐大的影象和影片充斥著我們的生活。我們需要對圖片進行檢索、分類等操作時,利用人工手段顯然是不現實的。於是,計算機視覺相關技術便應運而生,並且得到了快速的發展。本文以時下最流行的Python語言為工具,對影象處理技術的具體操作進行詳細講述,旨在讓零基礎的讀者也可以輕鬆上手!

01 SciPy
SciPy是建立在NumPy基礎上,用於數值運算的開源工具包。SciPy提供很多高效的操作,可以實現數值積分、最佳化、統計、訊號處理,以及對我們來說最重要的影象處理功能。接下來,本節會介紹SciPy中大量有用的模組。SciPy是一個開源工具包,可以從http://scipy.org/Download 下載。
02 影象導數
在整個影象處理的學習過程中可以看到,在很多應用中影象強度的變化情況是非常重要的資訊。強度的變化可以用灰度影象I(對於彩色影象,通常對每個顏色通道分別計算導數)的x和y的方嚮導數 和
和 進行描述。
進行描述。
影象的梯度向量為:
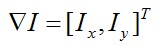
梯度有兩個重要的屬性,一個是梯度的大小:

它描述了影象變化的強弱,一是梯度的角度:

它描述了影象中在每個點(畫素)上強度變化最大的方向。NumPy中的arctan2()函式傳回弧度表示的有符號角度,角度的變化區間為 。
。
我們可以用離散近似的方式來計算影象的導數。影象的導數大多可以透過摺積簡單地實現:

對於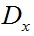 和
和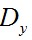 ,通常選擇Prewitt濾波器:
,通常選擇Prewitt濾波器:
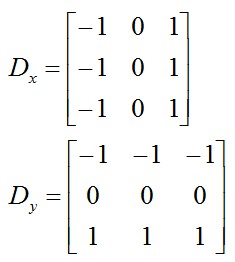
Prewitt邊緣運算元是一種邊緣樣板運算元,利用畫素點上下,左右鄰點灰度差,在邊緣處達到極值檢測邊緣,對噪聲具有平滑作用。由於邊緣點畫素的灰度值與其領域點畫素的灰度值有顯著不同,在實際應用中通常採用微分運算元和模板配匹方法檢測影象的邊緣。
或者使用Sobel濾波器,Sobel演演算法是一種較成熟的微分邊緣檢測演演算法,它計算簡單,且能產生較好的檢測效果,對噪聲具有平滑作用,可以提供較為精確的邊緣方向資訊。
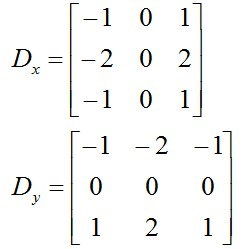
Sobel運算元是一階導數的邊緣檢測運算元,使用兩個方向運算元(垂直運算元和水平運算元),對影象進行摺積運算,得到兩個矩陣,再求這兩個矩陣對應位置的兩個數的均方根,得到一個新的矩陣,即為灰度影象矩陣中各個畫素點的梯度值。在演演算法實現過程中,透過3×3模板作為核與影象中的每個畫素點做摺積和運算,然後選取合適的閾值以提取邊緣。
其實影象的梯度可以用一階導數和二階偏導數來求解。但是影象以矩陣的形式儲存的,不能像數學理論中對直線或者曲線求導一樣,對一幅影象的求導相當於對一個平面、曲面求導。對影象的操作,我們採用模板對原影象進行摺積運算,從而達到我們想要的效果。而獲取一幅影象的梯度就轉化為:模板(Roberts、Prewitt、Sobel、Lapacian運算元)對原影象進行摺積,不過這裡的模板並不是隨便設計的,而是根據數學中求導理論推匯出來的。
這些導數濾波器可以使用scipy.ndimage.filters模組的標準摺積操作來簡單地實現。
程式碼為:
PIL Image numpy * matplotlib.pyplot plt scipy.ndimage filters im = array(Image.open().convert()) imx = zeros(im.shape) filters.sobel(imimx) imy = zeros(im.shape) filters.sobel(imimx) magnitude = sqrt(imx ** + imy ** ) fig = plt.figure(=()) plt.subplot() plt.axis() plt.imshow(implt.cm.gray) plt.subplot() plt.axis() plt.imshow(imxplt.cm.gray) plt.subplot() plt.axis() plt.imshow(imyplt.cm.gray) plt.subplot() plt.axis() plt.imshow(magnitudeplt.cm.gray) plt.show()
輸出結果為:


▲上述輸出結果分別是原始灰度影象、x導數影象、y導數影象、梯度大小影象
這種計算影象導數的方法有一些缺陷,在該方法中,濾波器的尺度需要隨著影象解析度的變化而變化。為了在影象噪聲方面更穩健,以及在任意尺度上計算導數,我們使用高斯導數濾波器:

其中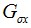 和
和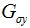 表示
表示 在x和y方向上的導數,
在x和y方向上的導數, 為標準差為σ的高斯函式。
為標準差為σ的高斯函式。
我們之前用於模糊的filters.gaussian_filter()函式可以接受額外的引數,用來計算高斯導數。可以簡單的按照下麵的方式來處理:
PIL Image numpy * matplotlib.pyplot plt scipy.ndimage filters im = array(Image.open().convert()) sigma = imx = zeros(im.shape) filters.gaussian_filter(im(sigmasigma)()imx) imy = zeros(im.shape) filters.gaussian_filter(im(sigmasigma)()imy) fig = plt.figure(=()) plt.subplot() plt.axis() plt.imshow(implt.cm.gray) plt.subplot() plt.axis() plt.imshow(imxplt.cm.gray) plt.subplot() plt.axis() plt.imshow(imyplt.cm.gray) plt.show()
輸出結果為:

(a)

(b)
上面輸出結果(a)、(b)中圖片依次為:原始灰度影象,x導數影象,y導數影象,而(a),(b)的區別為設定不同的標準差之後的高斯濾波處理影象。
作者:Hui
來源:專知(ID:Quan_Zhuanzhi),關於“用Python做影象處理”的更多圖文,可在專知檢視
參考文獻:
python計算機視覺程式設計:
http://yongyuan.name/pcvwithpython/
推薦閱讀
日本老爺爺堅持17年用Excel作畫,我可能用了假的Excel···
看完此文再不懂區塊鏈算我輸:手把手教你用Python從零開始建立區塊鏈
Q: 關於影象處理,你有哪些想法和經驗?
歡迎留言與大家分享
覺得不錯,請把這篇文章分享給你的朋友
轉載 / 投稿請聯絡:baiyu@hzbook.com
更多精彩文章,請在公眾號後臺點選“歷史文章”檢視

 知識星球
知識星球