作者丨許志欽、張耀宇
學校丨紐約大學阿布扎比分校博士後、紐約大學庫朗研究所訪問學者
研究方向丨計算神經科學、深度學習理論
在上一篇文章F-Principle:初探理解深度學習不能做什麼中,我們介紹瞭如何用一個統一的框架來初步理解深度學習的優勢與侷限。在這篇文章中,我們將探索如何利用我們對深度學習已有的理解來設計演演算法。我們期待這些初步的探索能對解決真實問題起到引導作用。
首先,我們回顧一下這個框架。我們的發現可以用一句話概括:深度學習傾向於優先使用低頻來擬合標的函式。我們將這個機制稱為 F-Principle(頻率原則)。
我們先用一個簡單的例子來理解 F-Principle。用一個深度神經網路(DNN)去擬合如下的紅色實線函式。訓練完後,該曲線能被深度網路(藍色點)很好地擬合。

我們感興趣的是 DNN 的訓練過程。如下圖動畫所示,紅色為標的函式的 FT(傅裡葉變換),藍色為網路輸出的 FT,每一幀表示一個訓練步,橫坐標是頻率,縱坐標是振幅。
我們發現,在訓練過程中,DNN 表示的函式的演化在頻域空間有一個清晰的規律,即頻率從低到高依次收斂。

部分讀者覺得 F-Principle 非常直觀,甚至非常顯然(trivial)。部分原因可能是因為 F-Principle 並不是一個陌生的概念,而是我們日常生活中經常都在用的一個原則。想象一下,如果讓一個人去記住一個沒見過的東西,一般比較粗糙的輪廓資訊會先被記住,然後再是很多細節。
沒錯,DNN 也正是使用了這樣的一個學習過程。舉一個例子,我們來訓練一個 DNN 來記住一張圖片。DNN 的輸入是一個位置坐標 (x,y),我們希望它輸出這個位置對應的灰度值。
下圖的一系列圖展示了不同訓練步數,DNN 學習到的影象,正如我們前面所猜測的從粗糙的輪廓到細節的學習過程。

然而!更多的人非常驚訝於 DNN 有這樣簡單的規則。特別地,在計算數學中,很多迭代格式都是先收斂高頻,例如 Jacobi 方法和 Gauss–Seidel 方法。由於低頻往往是比較重要的,因此高頻優先的原則造成了很多苦惱。於是許多研究者手動設計很多演演算法來提升收斂低頻的速度,比如多重網格法。
對於大部分 DNN,它並不需要任何顯示的條件或者手動設計,它自然有低頻優先的原則。舉個例子,考慮如下 Poisson 方程:

其中, 。它的真實解如下圖曲線所示:
。它的真實解如下圖曲線所示:

▲ 黑色為Poisson方程的真解,插圖裡紅色為真解的傅裡葉變換
真解中有三個比較顯著的頻率峰值。如果我們用 Jacobi 迭代去解這個方程,如下圖,高頻先收斂。

▲ Jacobi迭代:三個重要頻率點處的相對誤差與訓練步數的關係,紅色表示相對誤差小,高頻先收斂
如果我們用 DNN 來解這個方程,我們會得到完全不一樣的結果。DNN 的輸入為 x,我們用 DNN 的輸出去逼近真解 u(x)。損失函式採用 Poisson 方程的能量泛函。具體解的過程可以參見論文。如下圖所示,F-Principle 非常明顯,既低頻比高頻收斂得快很多。

▲ 寬度為1-4000-500-400-1的DNN:三個重要頻率點處的相對誤差與訓練步數的關係,紅色表示相對誤差小,低頻先收斂
一個自然的想法是,為了更快地解 Poisson 方程,我們可以先用 DNN 解出低頻部分。等低頻收斂好以後,將 DNN 的輸出作為 Jacobi 迭代的初值來繼續解 Poisson 方程。
在下圖中,我們展示了結合兩種方法的效果。下圖展示的是數值解和真實解之差的最大絕對值隨計算機執行時間的變化。
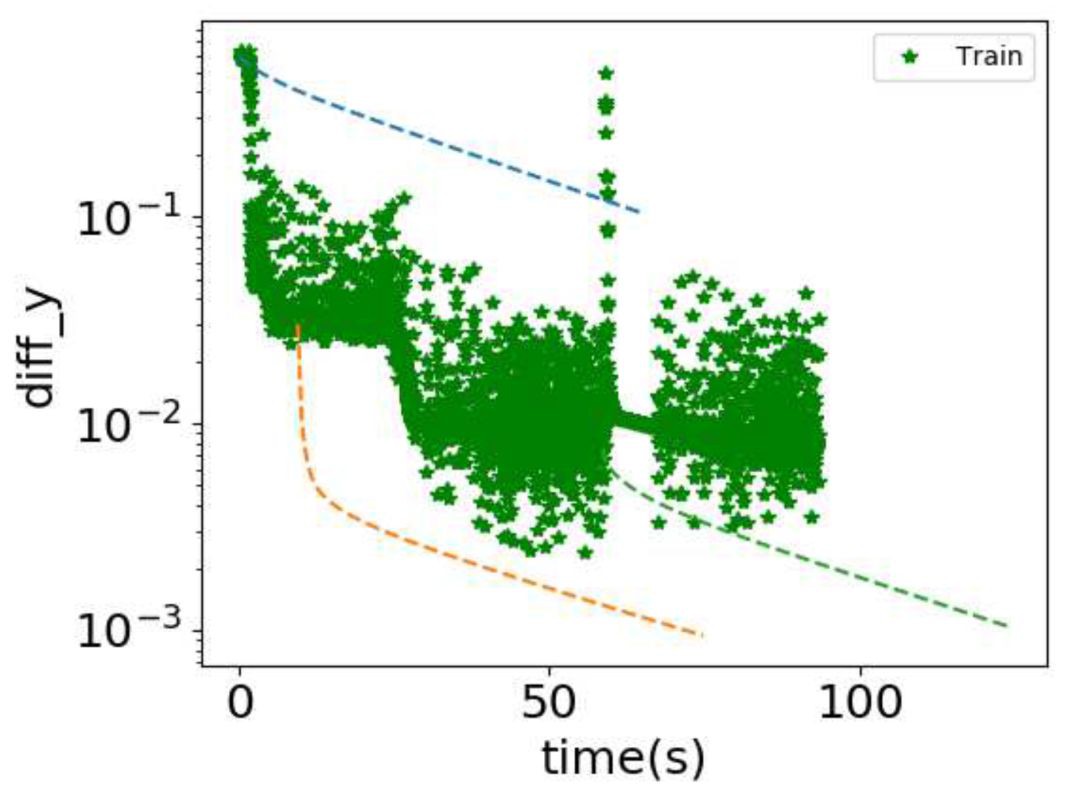
▲ 結合DNN與Jacobi來解Poisson方程。橫坐標:計算機執行時間。縱坐標:數值解和真實解之差的最大絕對值。綠色星號:DNN的結果。虛線:Jacobi方法繼續運算的結果,不同虛線表示選擇不同DNN訓練時刻的輸出作為初值
如果單純使用 DNN,綠色星號表明在一段時間後,DNN 的輸出振蕩很厲害。三條虛線的結果是在不同時刻使用 Jacobi 繼續運算的結果。最左邊的藍色虛線選擇的時刻過早,導致 Jacobi 方法需要花大時時間來收斂低頻,因此誤差下降很慢。最右邊的綠色虛線選擇的時刻過晚,導致大量時間花在 DNN 收斂高頻上。中間的橙色虛線剛好利用了 DNN 收斂好的低頻,並且馬上使用 Jacobi 方法快速收斂高頻,所以誤差在短時間內能下降最快。
在偏微分方程的數值問題中,有很多問題對於傳統演演算法是很困難的。很多研究工作已經開始探索如何使用 DNN 來解這些問題。
這個例子只是一個非常簡單地情況,對於用 F-Principle 的理解來幫助 DNN 應用在更複雜、更高維的問題中,仍然有非常多值得探討的問題。這個例子展示了在理解 DNN 的基礎上去使用 DNN,我們可以既利用 DNN 的強項,又能避免 DNN 的弱點。
參考文獻
Xu, Zhi-Qin John; Zhang, Yaoyu; Luo, Tao; Xiao, Yanyang & Ma, Zheng (2019), ‘Frequency principle: Fourier analysis sheds light on deep neural networks’, arXiv preprint arXiv:1901.06523.

點選以下標題檢視更多往期內容:
 知識星球
知識星球