關於作者：小一一，北京大學在讀碩士，研究方向為深度模型壓縮加速。個人主頁：http://yanjoy.win

■ 論文 | A Survey of Model Compression and Acceleration for Deep Neural Networks

■ 連結 | https://www.paperweekly.site/papers/1675

■ 作者 | Yu Cheng / Duo Wang / Pan Zhou / Tao Zhang

研究背景

在神經網路方面，早在上個世紀末，Yann LeCun 等人已經使用神經網路成功識別了郵件上的手寫郵編。至於深度學習的概念是由 Geoffrey Hinton 等人首次提出，而在 2012 年，Krizhevsky 等人採用深度學習演演算法，以超過第二名以傳統人工設計特徵方法準確率 10% 的巨大領先取得了 ImageNet 影象分類比賽冠軍。

此後的計算機視覺比賽已經被各種深度學習模型所承包。這些模型依賴於具有數百甚至數十億引數的深度網路，傳統 CPU 對如此龐大的網路一籌莫展，只有具有高計算能力的 GPU 才能讓網路得以相對快速訓練。

如上文中比賽用模型使用了 1 個包含 5 個摺積層和 3 個完全連線層的 6000 萬引數的網路。通常情況下，即使使用當時效能頂級的 GPU NVIDIA K40 來訓練整個模型仍需要花費兩到三天時間。對於使用全連線的大規模網路，其引數規模甚至可以達到數十億量級。

當然，為瞭解決全連線層引數規模的問題，人們轉而考慮增加摺積層，使全連線引數降低。隨之帶來的負面影響便是大大增長了計算時間與能耗。

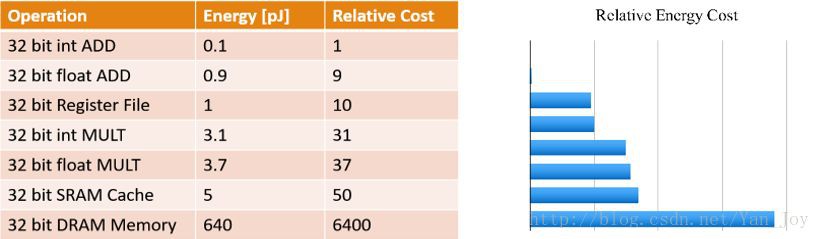
對於具有更多層和節點的更大的神經網路，減少其儲存和計算成本變得至關重要，特別是對於一些實時應用，如線上學習、增量學習以及自動駕駛。

在深度學習的另一端，即更貼近人們生活的移動端，如何讓深度模型在移動裝置上執行，也是模型壓縮加速的一大重要標的。

Krizhevsky 在 2014 年的文章中，提出了兩點觀察結論：摺積層佔據了大約 90-95% 的計算時間和引數規模，有較大的值；全連線層佔據了大約 5-10% 的計算時間，95% 的引數規模，並且值較小。這為後來的研究深度模型的壓縮與加速提供了統計依據。

一個典型的例子是具有 50 個摺積層的 ResNet-50 需要超過 95MB 的儲存器以及 38 億次浮點運算。在丟棄了一些冗餘的權重後，網路仍照常工作，但節省了超過 75％ 的引數和 50％ 的計算時間。

當然，網路模型的壓縮和加速的最終實現需要多學科的聯合解決方案，除了壓縮演演算法，資料結構、計算機體系結構和硬體設計等也起到了很大作用。本文將著重介紹不同的深度模型壓縮方法，併進行對比。

研究現狀

綜合現有的深度模型壓縮方法，它們主要分為四類： 

• 引數修剪和共享（parameter pruning and sharing） 

• 低秩因子分解（low-rank factorization） 

• 轉移/緊湊摺積濾波器（transferred/compact convolutional filters） 

• 知識蒸餾（knowledge distillation） 

基於引數修剪和共享的方法針對模型引數的冗餘性，試圖去除冗餘和不重要的項。基於低秩因子分解的技術使用矩陣/張量分解來估計深度學習模型的資訊引數。基於傳輸/緊湊摺積濾波器的方法設計了特殊的結構摺積濾波器來降低儲存和計算複雜度。知識蒸餾方法透過學習一個蒸餾模型，訓練一個更緊湊的神經網路來重現一個更大的網路的輸出。 

一般來說，引數修剪和共享，低秩分解和知識蒸餾方法可以用於全連線層和摺積層的 CNN，但另一方面，使用轉移/緊湊型摺積核的方法僅支援摺積層。

低秩因子分解和基於轉換/緊湊型摺積核的方法提供了一個端到端的流水線，可以很容易地在 CPU/GPU 環境中實現。

相反引數修剪和共享使用不同的方法，如向量量化，二進位制編碼和稀疏約束來執行任務，這導致常需要幾個步驟才能達到標的。

▲ 表1：不同模型的簡要對比

關於訓練協議，基於引數修剪/共享、低秩分解的模型可以從預訓練模型或者從頭開始訓練，因此靈活而有效。然而轉移/緊湊的摺積核和知識蒸餾模型只能支援從零開始訓練。

這些方法是獨立設計和相輔相成的。例如，轉移層和引數修剪和共享可以一起使用，並且模型量化和二值化可以與低秩近似一起使用以實現進一步的加速。

不同模型的簡要對比，如表 1 所示。下文針對這些方法做一簡單介紹與討論。

引數修剪和共享

根據減少冗餘（資訊冗餘或引數空間冗餘）的方式，這些引數修剪和共享可以進一步分為三類：模型量化和二進位制化、引數共享和結構化矩陣（structural matrix）。

量化和二進位制化

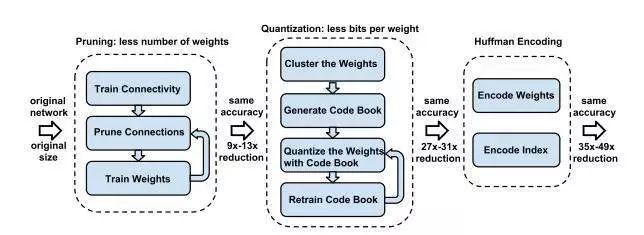
▲ 圖2

網路量化透過減少表示每個權重所需的位元數來壓縮原始網路。Gong et al. 對引數值使用 K-Means 量化。Vanhoucke et al. 使用了 8 位元引數量化可以在準確率損失極小的同時實現大幅加速。

Han S 提出一套完整的深度網路的壓縮流程：首先修剪不重要的連線，重新訓練稀疏連線的網路。然後使用權重共享量化連線的權重，再對量化後的權重和碼本進行霍夫曼編碼，以進一步降低壓縮率。如圖 2 所示，包含了三階段的壓縮方法：修剪、量化（quantization）和霍夫曼編碼。

修剪減少了需要編碼的權重數量，量化和霍夫曼編碼減少了用於對每個權重編碼的位元數。對於大部分元素為 0 的矩陣可以使用稀疏表示，進一步降低空間冗餘，且這種壓縮機制不會帶來任何準確率損失。這篇論文獲得了 ICLR 2016 的 Best Paper。 

在量化級較多的情況下準確率能夠較好保持，但對於二值量化網路的準確率在處理大型 CNN 網路，如 GoogleNet 時會大大降低。另一個缺陷是現有的二進位制化方法都基於簡單的矩陣近似，忽視了二進位制化對準確率損失的影響。

剪枝和共享

網路剪枝和共享起初是解決過擬合問題的，現在更多得被用於降低網路複雜度。

早期所應用的剪枝方法稱為偏差權重衰減（Biased Weight Decay），其中最優腦損傷（Optimal Brain Damage）和最優腦手術（Optimal Brain Surgeon）方法，是基於損失函式的 Hessian 矩陣來減少連線的數量。

他們的研究表明這種剪枝方法的精確度比基於重要性的剪枝方法（比如 Weight Decay 方法）更高。這個方向最近的一個趨勢是在預先訓練的 CNN 模型中修剪冗餘的、非資訊量的權重。

在稀疏性限制的情況下培訓緊湊的 CNN 也越來越流行，這些稀疏約束通常作為 l_0 或 l_1 範數調節器在最佳化問題中引入。 

剪枝和共享方法存在一些潛在的問題。首先，若使用了 l_0 或 l_1 正則化，則剪枝方法需要更多的迭代次數才能收斂，此外，所有的剪枝方法都需要手動設定層的超引數，在某些應用中會顯得很複雜。

▲ 圖3：剪枝和共享

設計結構化矩陣

該方法的原理很簡單：如果一個 m×n 階矩陣只需要少於 m×n 個引數來描述，就是一個結構化矩陣（structured matrix）。通常這樣的結構不僅能減少記憶體消耗，還能透過快速的矩陣-向量乘法和梯度計算顯著加快推理和訓練的速度。 

這種方法的一個潛在的問題是結構約束會導致精確度的損失，因為約束可能會給模型帶來偏差。另一方面，如何找到一個合適的結構矩陣是困難的。沒有理論的方法來推匯出來。因而該方法沒有廣泛推廣。

低秩分解和稀疏性

一個典型的 CNN 摺積核是一個 4D 張量，而全連線層也可以當成一個 2D 矩陣，低秩分解同樣可行。這些張量中可能存在大量的冗餘。所有近似過程都是逐層進行的，在一個層經過低秩濾波器近似之後，該層的引數就被固定了，而之前的層已經用一種重構誤差標準（reconstruction error criterion）微調過。這是壓縮 2D 摺積層的典型低秩方法，如圖 4 所示。

▲ 圖4：壓縮2D摺積層的典型低秩方法

使用低階濾波器加速摺積的時間已經很長了，例如，高維 DCT（離散餘弦變換）和使用張量積的小波系統分別由 1D DCT 變換和 1D 小波構成。

學習可分離的 1D 濾波器由 Rigamonti 等人提出，遵循字典學習的想法。Jaderberg 的工作提出了使用不同的張量分解方案，在文字識別準確率下降 1％ 的情況下實現了 4.5 倍加速。

一種 flatten 結構將原始三維摺積轉換為 3 個一維摺積，引數複雜度由 O(XYC)降低到 O(X+Y+C)，運算複雜度由 O(mnCXY) 降低到 O(mn(X+Y+C)。 

低階逼近是逐層完成的。完成一層的引數確定後，根據重建誤差準則對上述層進行微調。這些是壓縮二維摺積層的典型低秩方法，如圖 2 所示。

按照這個方向，Lebedev 提出了核張量的典型多項式（CP）分解，使用非線性最小二乘法來計算。Tai 提出了一種新的從頭開始訓練低秩約束 CNN 的低秩張量分解演演算法。它使用批次標準化（BN）來轉換內部隱藏單元的啟用。一般來說， CP 和 BN分解方案都可以用來從頭開始訓練 CNN。 

低秩方法很適合模型壓縮和加速，但是低秩方法的實現並不容易，因為它涉及計算成本高昂的分解操作。另一個問題是目前的方法都是逐層執行低秩近似，無法執行全域性引數壓縮，因為不同的層具備不同的資訊。最後，分解需要大量的重新訓練來達到收斂。

遷移/壓縮摺積濾波器

雖然目前缺乏強有力的理論，但大量的實證證據支援平移不變性和摺積權重共享對於良好預測效能的重要性。

使用遷移摺積層對 CNN 模型進行壓縮受到 Cohen 的等變群論（equivariant group theory）的啟發。使 x 作為輸入，Φ(·) 作為網路或層，T(·) 作為變換矩陣。則等變概念可以定義為：

即使用變換矩陣 T(·) 轉換輸入 x，然後將其傳送至網路或層 Φ(·)，其結果和先將 x 對映到網路再變換對映後的表徵結果一致。註意 T 和 T’ 在作用到不同物件時可能會有不同的操作。根據這個理論，將變換應用到層次或濾波器 Φ(·) 來壓縮整個網路模型是合理的。

使用緊湊的摺積濾波器可以直接降低計算成本。在 Inception 結構中使用了將 3×3 摺積分解成兩個 1×1 的摺積；SqueezeNet 提出用 1×1 摺積來代替 3×3 摺積，與 AlexNet 相比，SqueezeNet 建立了一個緊湊的神經網路，引數少了 50 倍，準確度相當。 

這種方法仍有一些小問題解決。首先，這些方法擅長處理廣泛/平坦的體系結構（如 VGGNet）網路，而不是狹窄的/特殊的（如 GoogleNet，ResidualNet）。其次，轉移的假設有時過於強大，不足以指導演演算法，導致某些資料集的結果不穩定。

知識蒸餾

利用知識轉移（knowledge transfer）來壓縮模型最早是由 Caruana 等人提出的。他們訓練了帶有偽資料標記的強分類器的壓縮/整合模型，並複製了原始大型網路的輸出，但是，這項工作僅限於淺模型。

後來改進為知識蒸餾，將深度和寬度的網路壓縮成較淺的網路，其中壓縮模型模擬複雜模型所學習的功能，主要思想是透過學習透過 softmax 獲得的類分佈輸出，將知識從一個大的模型轉移到一個小的模型。 

Hinton 的工作引入了知識蒸餾壓縮框架，即透過遵循“學生-教師”的正規化減少深度網路的訓練量，這種“學生-教師”的正規化，即透過軟化“教師”的輸出而懲罰“學生”。為了完成這一點，學生學要訓練以預測教師的輸出，即真實的分類標簽。這種方法十分簡單，但它同樣在各種影象分類任務中表現出較好的結果。 

基於知識蒸餾的方法能令更深的模型變得更加淺而顯著地降低計算成本。但是也有一些缺點，例如只能用於具有 Softmax 損失函式分類任務，這阻礙了其應用。另一個缺點是模型的假設有時太嚴格，其效能有時比不上其它方法。

討論與挑戰

深度模型的壓縮和加速技術還處在早期階段，目前還存在以下挑戰： 

• 依賴於原模型，降低了修改網路配置的空間，對於複雜的任務，尚不可靠；

• 透過減少神經元之間連線或通道數量的方法進行剪枝，在壓縮加速中較為有效。但這樣會對下一層的輸入造成嚴重的影響；

• 結構化矩陣和遷移摺積濾波器方法必須使模型具有較強的人類先驗知識，這對模型的效能和穩定性有顯著的影響。研究如何控制強加先驗知識的影響是很重要的；

• 知識精煉方法有很多優勢，比如不需要特定的硬體或實現就能直接加速模型。個人覺得這和遷移學習有些關聯。 

• 多種小型平臺（例如移動裝置、機器人、自動駕駛汽車）的硬體限制仍然是阻礙深層 CNN 發展的主要問題。相比於壓縮，可能模型加速要更為重要，專用晶片的出現固然有效，但從數學計算上將乘加法轉為邏輯和位移運算也是一種很好的思路。

量化實驗中問題與討論

實驗框架的選擇

TensorFlow 支援的是一種靜態圖，當模型的引數確定之後，便無法繼續修改。這對於逐階段、分層的訓練帶來了一定的困難。相比之下，Pytorch 使用了動態圖，在定義完模型之後還可以邊訓練邊修改其引數，具有很高的靈活性。這也是深度學習未來的發展方向。

目前的開發者版本 nightly 中，TensorFlow也開始支援動態圖的定義，但還未普及。 因此在選擇上，科研和實驗優先用 Pytorch，工程和應用上可能要偏 TensorFlow。 

聚類演演算法的低效性

聚類演演算法是量化的前提，sklearn 中提供了諸如 K-Means，Mean-shift，Gaussian mixtures 等可用的方法。

其中 K-Means 是一種簡單有效而較為快速的方法了。在個人電腦上，由於訓練網路引數規模較小，因而無法體現出其運算時間。在對 VGG 這樣大型的網路測試時，發現對於 256 個聚類中心，在 fc 的 4096∗4096 維度的全連線層進行聚類時，耗時超過 20 分鐘（沒有執行完便停止了），嚴重影響了演演算法的實用性。

目前的解決辦法是抽樣取樣，如對 1% 的引數進行聚類作為整體引數的聚類中心。這樣操作後聚類時間能縮短到 5 分鐘以內。 

有沒有一個更加簡便的方法呢？對於訓練好的一個模型，特別是經過 l2 正則化的，其引數分佈基本上可以看作是一個高斯分佈模型，對其進行擬合即可得到分佈引數。

這樣問題就轉化為：對一個特定的高斯分佈模型，是否能夠根據其引數直接得到聚類中心？

如果可以，那這個聚類過程將會大大縮短時間：首先對權重進行直方圖劃分，得到不同區間的引數分佈圖，再由此擬合高斯函式，最後用這個函式獲得聚類中心。這個工作需要一定的數學方法，這裡只是簡單猜想一下。

重訓練帶來的時間成本

我們日常說道的資料壓縮，是根據信源的分佈、機率進行的，特別是透過構建字典，來大大減少資訊冗餘。

這套方法直接使用在模型上，效果往往不好。一個最重要的原因就是引數雖然有著美妙的分佈，但幾乎沒有兩個相同的引數。在對 Alexnet 進行 gzip 壓縮後，僅僅從 233MB 下降到 216MB，遠不如文字以及影象壓縮演演算法的壓縮率。因此傳統方法難以解決深度學習的問題。 

剪枝量化雖好，但其問題也是傳統壓縮所沒有的，那就是重訓練所帶來的時間成本。這個過程就是人為為引數增加條件，讓網路重新學習降低 loss 的過程，因此也無法再重新恢覆成原始的網路，因為引數不重要，重要的是結果。

這個過程和訓練一樣，是痛苦而漫長的。又因為是逐層訓練，一個網路的訓練時間和層數密切相關。

Mnist 這種簡單任務，512∗512 的權重量化重訓練，由最開始的 8s 增加到 36s，增加了約 4 倍時間（不排除個人程式碼最佳化不佳的可能）。如果在 GPU 伺服器上，Alex 的時間成本可能還是勉強接受的，要是有 GoogleNet，ResNet 這種，真的是要訓到天荒地老了。

實現過程中，有很多操作無法直接實現，或者沒有找到簡便的方法，不得不繞了個彎子，確實會嚴重降低效能。

本文由 AI 學術社群 PaperWeekly 精選推薦，社群目前已改寫自然語言處理、計算機視覺、人工智慧、機器學習、資料挖掘和資訊檢索等研究方向，點選「閱讀原文」即刻加入社群！

點選標題檢視更多論文解讀： 

•   腦洞大開的機器視覺多領域學習模型結構

•   新型RNN：將層內神經元相互獨立以提高長程記憶

•   視覺跟蹤之端到端的光流相關濾波

• CycleGAN：圖片風格，想換就換

• 基於GAN的字型風格遷移

• 基於置信度的知識圖譜表示學習框架

▲ 戳我檢視招聘詳情

#崗 位 推 薦#

平安人壽AI研發團隊2018社會招聘、校園招聘全面啟動！