最近把最佳化演演算法跟動力學結合起來思考得越來越起勁了，這是最佳化演演算法與動力學系列的第三篇，我有預感還會有第四篇，敬請期待。

簡單來個劇情回顧：第一篇中我們指出了其實 SGD 相當於常微分方程（ODE）的數值解法：尤拉法；第二篇我們從數值解法誤差分析的角度，分析了為什麼可以透過梯度來調節學習率，因此也就解釋了 RMSprop、Adam 等演演算法中，用梯度調節學習率的原理。

本文將給出一個更統一的觀點來看待這兩個事情，並且試圖回答一個更本質的問題：為什麼是梯度下降？

註：本文的討論沒有涉及到動量加速部分。

梯度下降再述

前兩篇文章討論的觀點是“梯度下降相當於解 ODE”，可是我們似乎還沒有回答過，為什麼是梯度下降？它是怎麼來的？也就是說，之前我們只是在有了梯度下降之後，去解釋梯度下降，還沒有去面對梯度下降的起源問題。 

下降最快的方向

基本的說法是這樣的：梯度的反方向，是 loss 下降得最快的方向，所以要梯度下降。人們一般還會畫出一個等高線圖之類的示意圖，來解釋為什麼梯度的反方向是loss下降得最快的方向。

因此，很多人詬病 RMSprop 之類的自適應學習率最佳化器的原因也很簡單：因為它們改變了引數下降的方向，使得最佳化不再是往梯度方向下降，所以效果不好。 

但這樣解釋是不是足夠合理了呢？

再描述一下問題 

正式討論之前，我們把問題簡單定義一下：

1. 我們有一個標量函式 L(θ)≥0，這裡的引數 θ 可以是一個多元向量；

2. 至少存在一個點，使得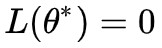，也就是說，L(θ) 的最小值就是 0；

3. 給定 L(θ) 的具體形式，我們當然希望找到讓 L(θ)=0 的 θ，就算不行，也希望找到一個 θ 讓 L(θ) 儘量小一些。

值得一提的是第 2 點，它其實並不是必要的，但有助於我們後面描述的一些探討。也就是說，第 2 點其實只是一個假設，要知道，隨便給我們一個函式，要我們求最小值的位置，但一般來說我們並不能事先知道它的最小值是多少。

但是在深度學習中，這一點基本是成立的，因為我們通常會把 loss 設定成非負，並且得益於神經網路強大的擬合能力，loss 很大程度上都能足夠接近於 0。

考慮loss的變化率

好，進入正題。假設在最佳化過程中引數 θ 按照某種軌跡 θ(t) 進行變化，那麼 L(θ) 也變成了 t 的函式 L(θ(t))。註意這裡的 t 不是真實的時間，它只是用來描述變化的引數，相當於迭代次數。 

現在我們考慮 L(θ(t)) 的變化率：

這裡就是 dθ/dt，⟨⋅⟩ 表示普通的內積。我們希望 L 越小越好，自然是希望上式右端為負數，而且絕對值越大越好。假如固定的模長，那麼要使得上式右端最小，根據內積的特點，∇θL 和的夾角應該要是 180 度，也就是：

這也就說明瞭，梯度的反方向確實是 loss 下降最快的方向。而根據第一篇文章，上式不就是梯度下降？於是我們就很乾脆地匯出了梯度下降了。並且將 (2) 代入到 (1) 中，我們得到：

這表明，只要學習率足夠小（模擬 ODE 模擬到足夠準確），並且 ∇θL≠0，那麼 L 就一定會下降，直到 ∇θL=0，這時候停留的位置，是個極小值點或者鞍點，理論上不可能是極大值點。

此外，我們經常用的是隨機梯度下降，mini-batch 的做法會帶來一定的噪聲，而噪聲在一定程度上能降低鞍點的機率（鞍點有可能對擾動不魯棒），所以通常隨機梯度下降效果比全量梯度下降要好些。

RMSprop再述

其實如果真的理解了上述推導過程，那麼讀者可以自己折騰出很多不同的最佳化演演算法出來。 

不止有一個方向

比如，雖然前面已經證明瞭梯度的反方向是 loss 下降最快的方向，但憑什麼就一定要往降得最快的的方向走呢？雖然梯度的反方向是堂堂正道，但也總有一些劍走偏鋒的，理論上只要我保證能下降就行了，比如我可以取：

註意 ∇θL 是一個向量，sign(∇θL) 指的是對每一個分量取符號函式，得到一個元素是 -1 或 0 或 1 的向量。這樣一來式 (1) 變為：

其中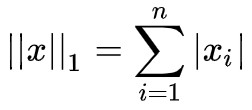表示向量的 L1 距離。這樣選取也保證了 loss 在下降，理論上它收斂在 ∇θL=0 之處。

其實我們還有（假設梯度分量非零）:

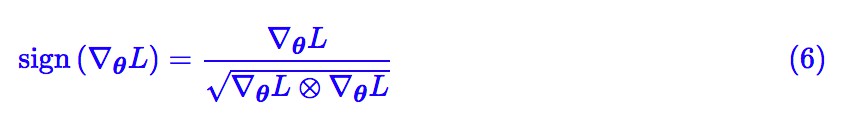
結合 (4) 和第二篇文章，再配合滑動平均，可以發現這一節說的就是 RMSprop 演演算法。

也就是說，自適應學習率最佳化器中，“學習率變成了向量，使得最佳化方向不再是梯度方向”根本不是什麼毛病，也就不應該是自適應學習率最佳化器被人詬病之處。

不走捷徑會怎樣

但事實上是，真的精細調參的話，通常來說自適應學習率最終效果真的是不如 SGD，說明自適應學習率最佳化器確實是有點毛病的。也就是說，如果你劍走偏鋒，雖然一開始你走的比別人快，後期你就不如別人了。 

毛病在哪呢？其實，如果是 Adagrad，那問題顯然是“太早停下來了”，因為它將歷史梯度求和了（而不是平均），導致後期學習率太接近 0 了；如果是上面說的 RMSprop，那麼問題是——“根本停不下來”。 

其實結合 (4) 和 (6) 我們得到：

這個演演算法什麼時候停下來呢？實際上它不會停，因為只要梯度分量非零，那麼對應的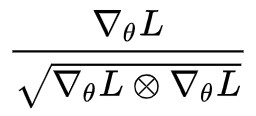的分量也非零（不是 1 就是 -1），從而在理論上看，這個演演算法並沒有不動點，所以它根本不會停。

為了緩解這個情況，RMSprop 在實際使用的時候，採取了對分母滑動平均、加上 epsilon（防止除零錯誤）這兩個技巧。

但這隻能算是緩解了問題，用 ODE 的話說就是“這個 ODE 並不是漸近穩定的”，所以終究會經常與區域性最優點插肩而過。這才是自適應學習率演演算法的問題。

一點搗鼓

前面說了，如果真的理解過這個過程，其實自己都可以搗鼓出一些“獨創的”最佳化演演算法出來，順便還分析收斂情況。下麵介紹我自己的一個搗鼓過程，還讓我誤以為是一個能絕對找出全域性最優點的最佳化器。

觀看下麵內容之前，請確保自己已經理解前述內容，否則可能造成誤導。

以全域性最優為導向

這個搗鼓的出發點在於，不管是 (2)（對應的收斂速率為 (3)）還是 (7)（對應的收斂速率為 (5)），就算它們能收斂，都只能保證 ∇θL=0 ，無法保證是全域性最優點（也就是不一定能做到 L(θ)=0）。

於是一個很簡單的想法是：既然我們已經知道了最小值是零，為什麼不把這個資訊加上去呢？ 

於是類比前面的思考過程，我們可以考慮：

這時候式 (1) 變得非常簡單：

這隻是一個普通的線性微分方程，而且解是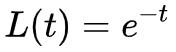，隨著 t→+∞，L(t)→0，也就是說 loss 一定能收斂到零。

真有這樣的好事？

當然沒有，我們來看式 (8) ，如果跑到了一個區域性最優點，滿足 ∇θL=0, L>0，那麼式 (8) 的右端就是負無窮了，這在理論上沒有問題，但是在數值計算上是無法實現的。

開始我以為這個問題很容易解決，似乎對分母加個 epsilon 避開原點就行了。但進一步分析才發現，這個問題是致命性的。 

為了觀察原因，我們把式 (8) 改寫為：

問題就在於 1/||∇θL|| 會變得無窮大（出現了奇點），那能不能做個截斷？比如考慮：

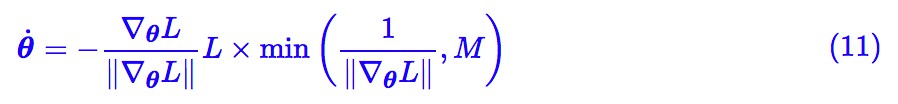
其中 M≫0 是個常數，這樣就繞開了奇點。這樣子做倒是真的能繞開一些區域性最優點，比如下麵的例子：

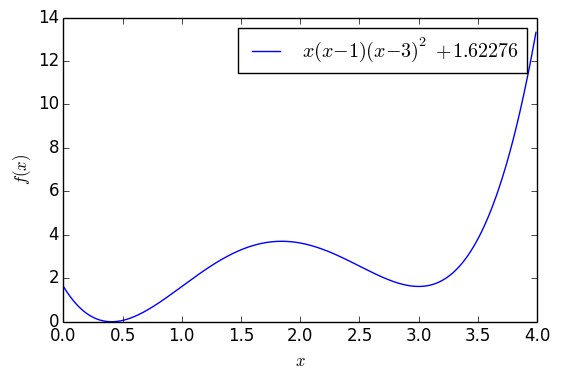
▲ 含有兩個極小值點的一元函式

這個函式大約在 x=0.41 之間有一個全域性最優點，函式值能取到 0，但是在 x=3 的時候有一個次最優點。如果以 x0=4 為初始值，單純是用梯度下降的話，那麼基本上都會收斂到 x=3，但是用 (11)，還是從 x0=4 出發，那麼經過一定振蕩後，最終能收斂到 x=0.41 附近：

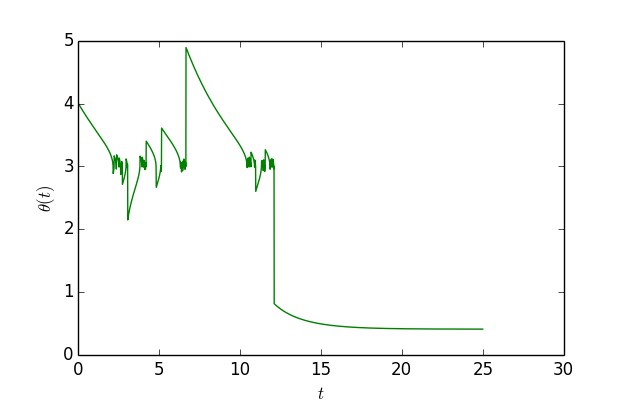
▲ 模擬“獨創版”梯度下降軌跡

可以看到，開始確實會在 x=3 附近徘徊，振蕩一段時間後就跳出來了，到了 x=0.41 附近。作圖程式碼：

然而，看上去很美好，實際上它沒有什麼價值，因為真的要保證跳出所有的區域性最優點，M 必須足夠大（這樣才能跟原始的 (10) 足夠接近），而且迭代步數足夠多。

但如果真能達到這個條件，其實還不如我們自己往梯度下降中加入高斯噪聲，因為在第一篇文章我們已經表明，如果假設梯度的噪聲是高斯的，那麼從機率上來看，總能達到全域性最優點（也需要迭代步數足夠多）。所以，這個看上去很漂亮的玩意，並沒有什麼實用價值。

文章小結

好了，哆裡哆嗦搗鼓了一陣，又水了一篇文章。個人感覺從動力學角度來分析最佳化演演算法是一件非常有趣的事情，它能讓你以一種相對輕鬆的角度來理解最佳化演演算法的魅力，甚至能將很多方面的知識聯絡起來。

一般的理解最佳化演演算法的思路，是從凸優化出發，然後把凸最佳化的結果不嚴格地用到非凸情形中。我們研究凸最佳化，是因為“凸性”對很多理論證明都是一個有力的條件，然而深度學習幾乎處處都是非凸的。

既然都已經是非凸了，也就是凸最佳化中的證明完備的這一優點已經不存在了，我覺得倒不如從一個更輕鬆的角度來看這個事情。這個更輕鬆的角度，就是動力系統，或者說常微分方程組。

事實上，這個視角的潛力很大，包括 GAN 的收斂分析，以及膾炙人口的“神經 ODE”，都終將落到這個視角來。當然這些都是後話了。