深度學習模型

1. Factorization-machine (FM) 

FM 模型可以看成是線性部分的 LR，還有非線性的特徵組合 xixj 交叉而成，表示如下：

其中 vi 是第 i 維特徵的隱向量，長度 k<

▲ 圖1：FM模型結構

圖 1 是從神經網路的角度表示 FM， 可以看成底層為特徵維度為 n 的離散輸入，經過 embedding 層後，對 embedding 層線性部分（LR）和非線性部分（特徵交叉部分）累加後輸出。

FM 等價於 FM + embedding，待學習的引數如下： 

• LR 部分：1+n

• embedding 部分：n*k

FM 下文中將作為各種網路模型的基礎元件。

2. Deep Neural Network (DNN) 

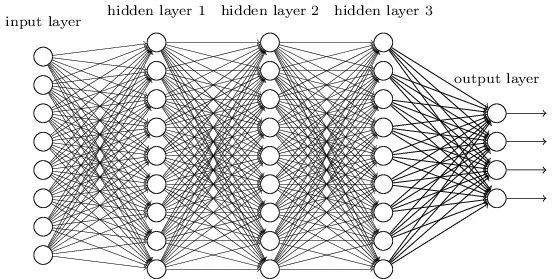
▲ 圖2：DNN模型結構

圖 2 是經典的 DNN 網路， 結構上看就是傳統的多層感知機（MultiLayer Perceptron，簡稱 MLP）。

在 MLP 網路中，輸入是原始的特徵 n 維特徵空間，假設第一層隱層節點數為 H1，第二層為 H2，以此類推。在第一層網路中，需要學習的引數就是 n*H1。

對於大多數 CTR 模型來說，特徵體系都極其龐大而且稀疏，典型的特徵數量級 n 從百萬級到千萬級到億級甚至更高，這麼大規模的 n 作為網路輸入在 CTR 預估的工業界場景中是不可接受的。

下麵要講到的大多數深度學習 CTR 網路結構，都圍繞著如何將 DNN 的高維離散輸入，透過 embedding 層變成低維稠密的輸入工作來展開。

DNN 待學習引數： 

n*H1+H1*H2+H2*H3+H3*o

o 為輸出層大小，在 CTR 預估中為 1。

DNN（後文稱 MLP）也將作為下文各種模型的基礎元件之一。

3. Factorization-machine supported Neural Networks (FNN) 

在上述的 DNN 中，網路的原始輸入是全部原始特徵，維度為 n，通常都是百萬級以上。然而特徵維度 n 雖然空間巨大，但如果歸屬到每個特徵所屬的 field（維度為 f），通常 f 維度會小很多。

如果有辦法將每個特徵用其所屬的 field 來表示，原始輸入將大大減少不少。Factorisation-machine Supported Neural Networks，簡稱 FNN 就是基於這種思想提出來的。

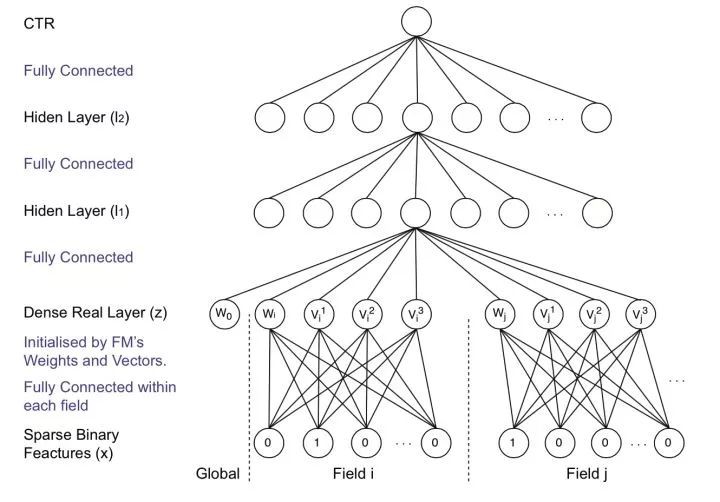
▲ 圖3：FNN模型結構

FNN 假設每個 field 有且只有一個值為 1，其他均為 0。x 為原始輸入的特徵，它是大規模離散稀疏的。它可以分成 n 個 field，每一個 field 中，只有一個值為 1，其餘都為 0（即 one hot）。 

field i 的輸入可以表示成 x[start_i: end_i]，Wi 為field i 的 embedding 矩陣。z為 embedding 後的向量，是一個 k 維的向量，它由一次項 wi ，二次項 vi=(vi1,vi2,…vik) 組成，其中 k 是 FM 中二次項的向量的維度。而後面的 l1，l2 則為神經網路的全連線層的表示。 

除此之外，FNN 還具有以下幾個特點： 

FM 引數需要預訓練 

FM 部分的 embedding 需要預先進行訓練，所以 FNN 不是一個 end-to-end 模型。在其他論文中，有試過不用 FM 初始化 embedding，而用隨機初始化的方法，要麼收斂速度很慢，要麼無法收斂。有興趣的同學可以實驗驗證下。 

無法擬合低階特徵 

FM 得到的 embedding 向量直接 concat 連線之後作為 MLP 的輸入去學習高階特徵表達，最終的 DNN 輸出作為 CTR 預估值。因此，FNN 對低階資訊的表達比較有限。 

每個 field 只有一個非零值的強假設 

FNN 假設每個 fileld 只有一個值為非零值，如果是稠密原始輸入，則 FNN 失去意義。對於一個 fileld 有幾個非零值的情況，例如使用者標簽可能有多個，一般可以做 average/sum/max 等處理。 

本質上講，FNN = LR+DEEP = LR + embedding + MLP，引數如下：

• LR 部分： 1+n

• embedding 部分： n*k

• MLP 部分： f*k*H1+H1*H2+H2 

可以看到，對比 DNN，在進入 MLP 部分之前，網路的輸入由 n 降到了 f*k（f 為 field 個數，幾十到幾百之間，k 為隱向量維度，一般 0~100）。

4. Product-based Neural Network (PNN) 

FNN 的 embedding 層直接 concat 連線後輸出到 MLP 中去學習高階特徵。

PNN，全稱為 Product-based Neural Network，認為在 embedding 輸入到 MLP 之後學習的交叉特徵表達並不充分，提出了一種 product layer 的思想，既基於乘法的運算來體現體徵交叉的 DNN 網路結構，如圖 4 所示。

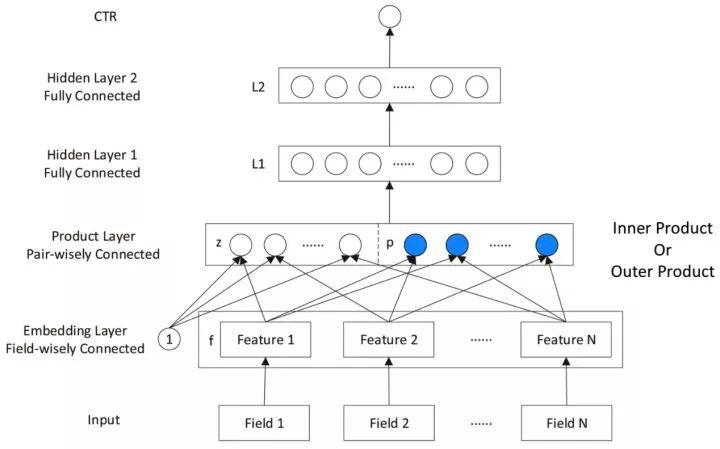
▲ 圖4：PNN模型結構

對比 FNN 網路，PNN 的區別在於中間多了一層 Product Layer 層。Product Layer 層由兩部分組成，左邊 z 為 embedding 層的線性部分，右邊為 embedding 層的特徵交叉部分。

除了 Product Layer 不同，PNN 和 FNN 的 MLP 結構是一樣的。這種 product 思想來源於，在 CTR 預估中，認為特徵之間的關係更多是一種 and“且”的關係，而非 add”加”的關係。例如，性別為男且喜歡遊戲的人群，比起性別男和喜歡遊戲的人群，前者的組合比後者更能體現特徵交叉的意義。

根據 product 的方式不同，可以分為 inner product (IPNN) 和 outer product (OPNN)，如圖 5 所示。

▲ 圖5：PNN (左圖 IPNN，右圖 OPNN)

Product Layer 的輸出為：

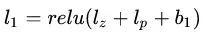
Inner Product-based Neural Network 

IPNN 的叉項使用了內積 g(fi, fj) = 。f 個 filed，兩兩求內積共計交叉項 p 部分的引數共 f*(f-1)/2（f 為特徵的 field 個數，原始論文裡用的 N）個，線性部分 z 部分引數共 f*k 個。需要學習的引數為： 

• FM 部分：1+ n + n*k 

• product部分：(f*k + f*(f-1)/2)*H1 

• MLP 部分：H1*H2+H2*1 

Outer Product-based Neural Network 

OPNN 用矩陣乘法來表示特徵的交叉，g(fi, fj)=fifit。f 個 field 兩兩求矩陣乘法，交叉項 p 共 f*(f-1)/2*k*k 個引數。線性部分 z 部分引數共 f*k 個。需要學習的引數為：

• FM 部分： 1+ n + n*k

• product 部分：(f*k + f*(f-1)/2*k*k)*H1

• MLP 部分：H1*H2+H2*1

5. Wide & Deep Learning (Wide & Deep) 

前面介紹的兩種變體 DNN 結構 FNN 和 PNN，都在 embedding 層對輸入做處理後輸入 MLP，讓神經網路充分學習特徵的高階表達，deep 部分是有了，對高階的特徵學習表達較強，但 wide 部分的表達是缺失的，模型對於低階特徵的表達卻比較有限。

Google 在 2016 年提出了大名鼎鼎的 Wide & Deep 結構正是解決了這樣的問題。Wide & Deep 結合了 Wide 模型的優點和 Deep 模型的優點，網路結構如圖 6 所示，Wide 部分是 LR 模型，Deep 部分是 DNN 模型。

▲ 圖6：Wide & Deep 模型結構

在這個經典的 Wide & Deep 模型中，Google 提出了兩個概念，Generalization（泛化性）和 Memory（記憶性）。 

Memory（記憶性） 

Wide 部分長處在於學習樣本中的高頻部分，優點是模型的記憶性好，對於樣本中出現過的高頻低階特徵能夠用少量引數學習；缺點是模型的泛化能力差，例如對於沒有見過的 ID 類特徵，模型學習能力較差。 

Generalization（泛化性） 

Deep 部分長處在於學習樣本中的長尾部分，優點是泛化能力強，對於少量出現過的樣本甚至沒有出現過的樣本都能做出預測（非零的 embedding 向量）;缺點是模型對於低階特徵的學習需要用較多參才能等同 Wide 部分效果，而且泛化能力強某種程度上也可能導致過擬合出現 bad case。

除此之外，Wide & Deep 模型還有如下特點：

人工特徵工程 

LR 部分的特徵，仍然需要人工設計才能保證一個不錯的效果。因為 LR 部分是直接作為最終預測的一部分，如果作為 Wide 部分的 LR 特徵工程做的不夠完善，將影響整個 Wide & Deep 的模型精度。

聯合訓練 

模型是 end-to-end 結構，Wide 部分和 Deep 部分是聯合訓練的。

Embedding 層 Deep 部分單獨佔有 

LR 部分直接作為最後輸出，因此 embedding 層是 Deep 部分獨有的。

Wide & Deep 等價於 LR + embedding + MLP，需要學習的網路引數有： 

• LR: 1+n 

• embedding 部分：n*k 

• MLP 部分：f*k*H1 + H1*H2 + H2*1 

6. Factorization-Machine based Neural Network (DeepFM) 

Google 提出的 Wide & Deep 框架固然強大，但由於 Wide 部分是個 LR 模型，仍然需要人工特徵工程。

Wide & Deep 給整個學術界和工業界提供了一種框架思想。基於這種思想，華為諾亞方舟團隊結合 FM 相比 LR 的特徵交叉的功能，將 Wide & Deep 部分的 LR 部分替換成 FM 來避免人工特徵工程，於是有了 DeepFM，網路結構如圖 7 所示。

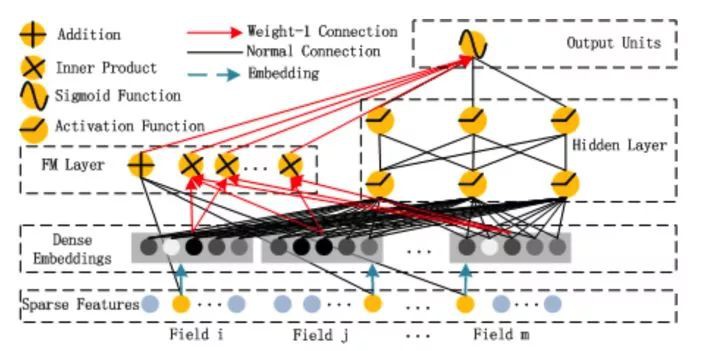
▲ 圖7：DeepFM 模型結構

比起 Wide & Deep 的 LR 部分，DeepFM 採用 FM 作為 Wide 部分的輸出，FM 部分如圖 8 所示。

▲ 圖8：DeepFM 模型中的 FM 部分結構

除此之外，DeepFM 還有如下特點： 

低階特徵表達 

Wide 部分取代 WDL 的 LR，比 FNN 和 PNN 更能捕捉低階特徵資訊。

Embedding 層共享 

Wide & Deep 部分的 embedding 層得需要針對 Deep 部分單獨設計；而在 DeepFM 中，FM 和 Deep 部分共享 embedding 層，FM 訓練得到的引數既作為 Wide 部分的輸出，也作為 DNN 部分的輸入。 

end-end訓練 

embedding 和網路權重聯合訓練，無需預訓練和單獨訓練。

DeepFM 等價於 FM + embedding + DNN：

• FM 部分：1+n

• embedding 部分：n*k

• DNN 部分：f*k*H1 + H1*H2+H1 

透過 embedding 層後，FM 部分直接輸出沒有引數需要學習，進入 DNN 部分的引數維度從原始 n 維降到 f*k 維。 

7. Neural Factorization Machines (NFM) 

前面的 DeepFM 在 embedding 層後把 FM 部分直接 concat 起來（f*k 維，f 個 field，每個 filed 是 k 維向量）作為 DNN 的輸入。

Neural Factorization Machines，簡稱 NFM，提出了一種更加簡單粗暴的方法，在 embedding 層後，做了一個叫做 BI-interaction 的操作，讓各個 field 做 element-wise 後 sum 起來去做特徵交叉，MLP 的輸入規模直接壓縮到 k 維，和特徵的原始維度 ｎ 和特徵 field 維度 f 沒有任何關係。

網路結構如圖 9 所示：

▲ 圖9：NFM 模型結構

這裡論文只畫出了其中的 Deep 部分，Wide 部分在這裡省略沒有畫出來。

Bi-interaction 聽名字很高大上，其實操作很簡單：就是讓 f 個 field 兩兩 element-wise 相乘後，得到 f*(f-1)/2 個向量，然後直接 sum 起來，最後得到一個 k 維的向量。所以該層沒有任何引數需要學習。 

NFM 等價於 FM + embedding + MLP，需要學習的引數有： 

• FM部分：1+n

• embedding部分：n*k

• MLP部分：k*H1 + H1*H2+…+Hl*1 

NFM 在 embedding 做了 bi-interaction 操作來做特徵的交叉處理，優點是網路引數從 n 直接壓縮到 k（比 FNN 和 DeepFM 的 f*k 還少），降低了網路複雜度，能夠加速網路的訓練得到模型；但同時這種方法也可能帶來較大的資訊損失。 

8. Attention Neural Factorization Machines (AFM) 

前面提到的各種網路結構中的 FM 在做特徵交叉時，讓不同特徵的向量直接做交叉，基於的假設是各個特徵交叉對 CTR 結果預估的貢獻度是一樣的。這種假設其實是不合理的，不同特徵在做交叉時，對 CTR 預估結果的貢獻度是不一樣的。

Attention Neural Factorization Machines，簡稱 NFM 模型，利用了近年來在影象、NLP、語音等領域大獲成功的 attention 機制，在前面講到的 NFM 基礎上，引入了 attention 機制來解決這個問題。

AFM 的網路結構如圖 10 所示。和 NFM 一樣，這裡也省略了 Wide 部分，只畫出了 Deep 部分結構。

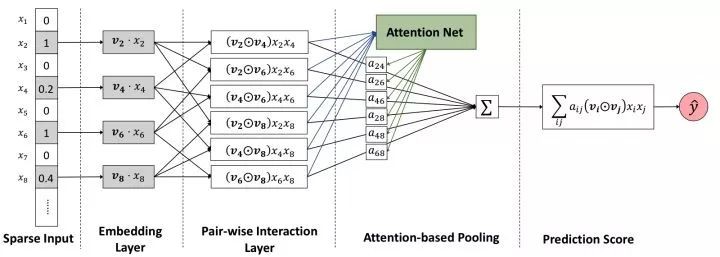
▲ 圖10：AFM 模型結構

AFM 的 embedding 層後和 NFM 一樣，先讓 f 個 field 的特徵做了 element-wise product 後，得到 f*(f-1)/2 個交叉項。

和 NFM 直接把這些交叉項 sum 起來不同，AFM 引入了一個 Attention Net，認為這些交叉特徵項每個對結果的貢獻是不同的，例如 xi 和 xj 的權重重要度，用 aij 來表示。

從這個角度來看，其實 AFM 就是個加權累加的過程。Attention Net 部分的權重 aij 不是直接學習，而是透過如下公式表示：

這裡 t 表示 attention net 中的隱層維度，k 和前面一樣，為 embedding 層的維度。所以這裡需要學習的引數有 3 個，W, b, h，引數個數共 t*k+2*t 個。

得到 aij 權重後，對各個特徵兩兩點積加權累加後，得到一個 k 維的向量，引入一個簡單的引數向量 pT，維度為 k 進行學習，和 Wide 部分一起得到最終的 AFM 輸出。

總結 AFM 的網路結構來說，有如下特點： 

Attention Network 

AFM 的亮點所在，透過一個 Attention Net 生成一個關於特徵交叉項的權重，然後將 FM 原來的二次項直接累加，變成加權累加。本質上是一個加權平均，學習 xjxj 的交叉特徵重要性。 

Deep Network 

沒有 Deep，卒。 

Attention Net 學習得到的交叉項直接學些個 pt 引數就輸出了，少了 DNN 部分的表達，對高階特徵部分的進一步學習可能存在瓶頸。另外，FFM 其實也引入了 field 的概念去學習 filed 和 featrue 之間的權重。

沒有了 Deep 部分的 AFM，和最佳化的 FFM 上限應該比較接近。 

AFM 等價於 FM + embedding + attention + MLP（一層），需要學習的引數有： 

• FM部分引數：1+n

• Embedding部分引數：n*k 

• Attention Network部分引數：k*t + t*2

• MLP部分引數：k*1

9. Deep⨯ Network (DCN) 

在 CTR 預估中，特徵交叉是很重要的一步，但目前的網路結構，最多都只學到二級交叉。

LR 模型採用原始人工交叉特徵，FM 自動學習 xi 和 xj 的二階交叉特徵，而 PNN 用 product 方式做二階交叉，NFM 和 AFM 也都採用了 Bi-interaction 的方式學習特徵的二階交叉。對於更高階的特徵交叉，只有讓 Deep 去學習了。

為解決這個問題，Google 在 2017 年提出了 Deep & Cross Network，簡稱 DCN 的模型，可以任意組合特徵，而且不增加網路引數。圖 11 為 DCN 的結構。

▲ 圖11：DCN 模型結構

整個網路由 4 部分組成： 

Embedding and Stacking Layer 

之所以不把 embedding 和 stacking 分開來看，是因為很多時候，embedding 和 stacking 過程是分不開的。

前面講到的各種 XX-based FM 網路結構，利用 FM 學到的 v 向量可以很好地作為 embedding。

而在很多實際的業務結構，可能已經有了提取到的 embedding 特徵資訊，例如影象的特徵 embedding，text 的特徵 embedding，item 的 embedding 等，還有其他連續值資訊，例如年齡，收入水平等，這些 embedding 向量 stack 在一起後，一起作為後續網路結構的輸入。

當然，這部分也可以用前面講到的 FM 來做 embedding。為了和原始論文保持一致，這裡我們假設 X0 向量維度為 d（上文的網路結構中為 k），這一層的做法就是簡單地把各種 embedding 向量 concat 起來。

Deep Layer Network

在 Embedding and Stacking Layer 之後，網路分成了兩路，一路是傳統的 DNN 結構。表示如下：

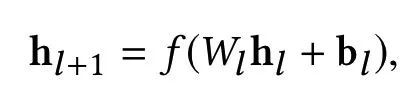
為簡化理解，假設每一層網路的引數有 m 個，一共有 Ld 層，輸入層由於和上一層連線，有 d*m 個引數（d 為 x0 向量維度），後續的 Ld-1 層，每層需要 m*(m+1) 個引數，所以一共需要學習的引數有 d*m+m*(m+1)*(Ld-1)。最後的輸出也是個 m 維向量 Hl2。

Cross Layer Network 

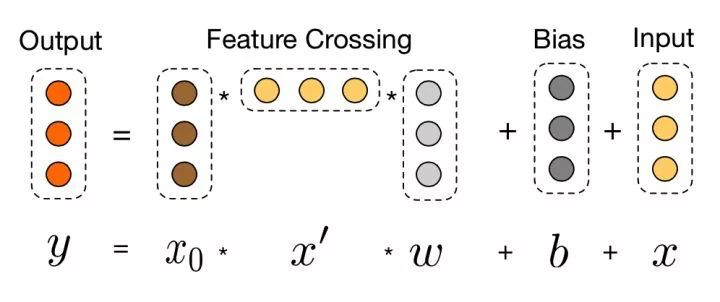
Embedding and Stacking Layer 輸入後的另一路就是 DCN 的重點工作了。假設網路有 L1 層，每一層和前一層的關係可以用如下關係表示：

可以看到 f 是待擬合的函式，xl 即為上一層的網路輸入。需要學習的引數為 wl 和 bl，因為 xl 維度為 d， 當前層網路輸入 xl+1 也為 d 維，待學習的引數 wl 和 bl 也都是 d 維度向量。

因此，每一層都有 2*d 的引數（w 和 b）需要學習，網路結構如下：

經過 Lc 層的 Cross Layer Network 後，在該 layer 最後一層 Lc 層的輸出為 Lc2 的 d 維向量。

Combination Output Layer 

經過 Cross Network 的輸出 XL1（d 維）和 Deep Network 之後的向量輸入（m 維）直接做 concat，變為一個 d+m 的向量，最後套一個 LR 模型，需要學習引數為 1+d+m。 

總結起來，DCN 引入的 Cross Network 理論上可以表達任意高階組合，同時每一層保留低階組合，引數的向量化也控制了模型的複雜度。 

DCN 等價於 embedding + cross + deep + LR：

• embedding 部分引數：根據情況而定

• cross 部分引數：2*d*Lc（Lc 為 cross 網路層數）

• deep 部分引數：d*(m+1)+m*(m+1)*(Ld-1)，Ld 為深度網路層數，m 為每層網路引數

• LR 部分引數：1+d+m

10. Deep Interest Network (DIN) 

最後介紹阿裡在 2017 年提出的 Deep Interest Network，簡稱 DIN 模型。與上面的 FNN，PNN 等引入低階代數正規化不同，DIN 的核心是基於資料的內在特點，引入了更高階的學習正規化。

使用者的興趣是多種多樣的，從數學的角度來看，使用者的興趣在興趣空間是一個多峰分佈。在預測 CTR 時，使用者 embedding 表示的興趣維度，很多是和當前 item 是否點選無關的，只和使用者興趣中的區域性資訊有關。

因此，受 attention 機制啟發，DIN 在 embedding 層後做了一個 action unit 的操作，對使用者的興趣分佈進行學習後再輸入到 DNN 中去，網路結構如圖 12所示：

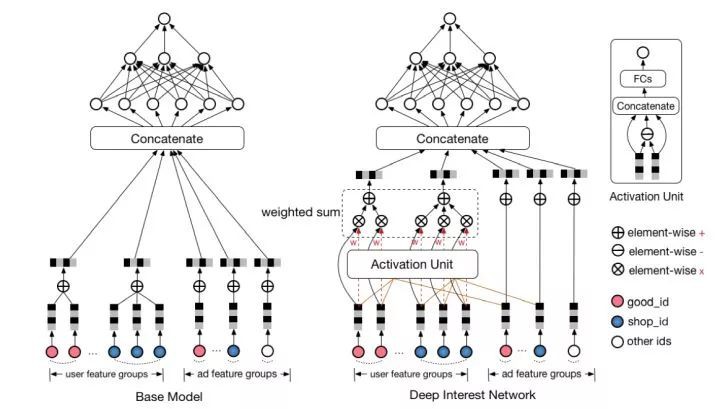
▲ 圖12：DIN 模型結構

DIN 把使用者特徵、使用者歷史行為特徵進行 embedding 操作，視為對使用者興趣的表示，之後透過 attention network，對每個興趣表示賦予不同的權值。 

• Vu：表示使用者最終向量 

• Vi：表示使用者興趣向量（shop_id, good_id..） 

• Va：表示廣告表示向量 

• Wi: 對於候選廣告，attention 機制中該興趣的權重

可以看到，對於使用者的每個興趣向量 Vi，都會透過學習該興趣的權重 Vi, 來作為最終的使用者表示。

寫在最後

前面介紹了 10 種深度學習模型的網路結構，總結起來如下所表示：

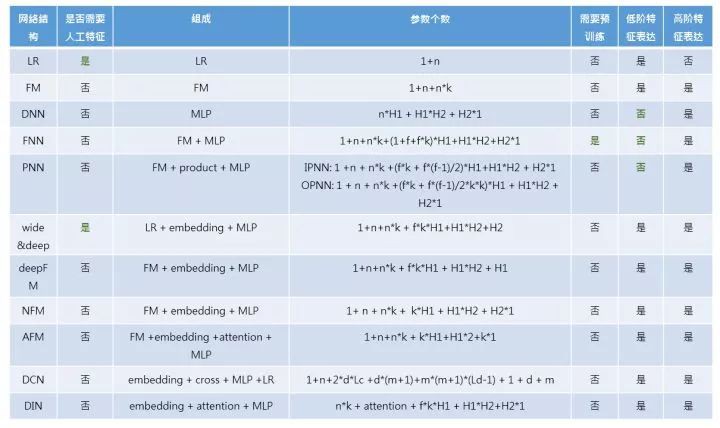
各種 CTR 深度模型看似結構各異，其實大多數可以用如下的通用正規化來表達：

input->embedding：把大規模的稀疏特徵 ID 用 embedding 操作對映為低維稠密的 embedding 向量。 

embedding 層向量：concat, sum, average pooling 等操作，大部分 CTR 模型在該層做改造。

embedding->output：通用的 DNN 全連線框架，輸入規模從 n 維降為 k*f 維度甚至更低。

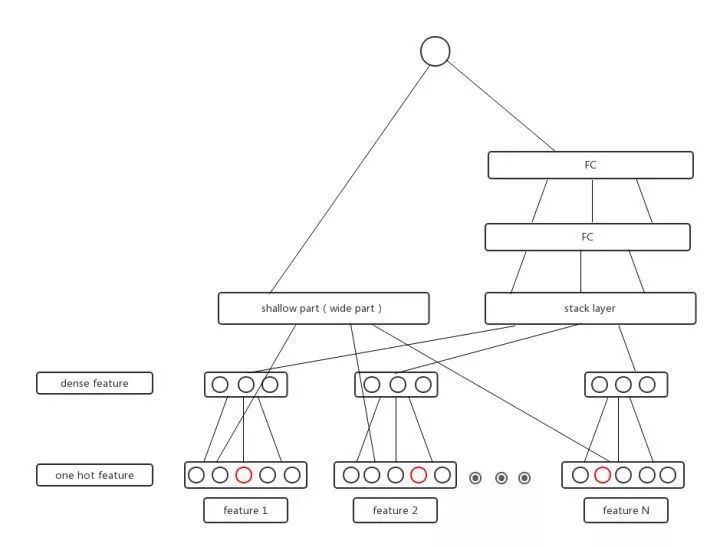
▲ 圖13：通用深度學習模型結構

其中，embedding vector 這層的融合是深度學習模型改造最多的地方，該層是進入深度學習模型的輸入層，embedding 融合的質量將影響 DNN 模型學習的好壞。

個人總結大體有以下 4 種操作，當然後續可能會有越來越多其他的變形結構。

▲ 圖14：embedding 層融合方式

另外，DNN 部分，業界也有很多或 state-of-art 或很 tricky 的方法，都可以在裡面進行嘗試，例如 dropout，在 NFM 的 Bi-interaction 中可以嘗試以一定機率 dropout 掉交叉特徵增前模型的泛化能力等。

結語

CTR 預估領域不像影象、語音等領域具有連續、稠密的資料以及空間、時間等的良好區域性相關性，CTR 預估中的大多數輸入都是離散而且高維的，特徵也分散在少量不同的 field 上。

要解決這樣的一個深度學習模型，面臨的第一個問題是怎麼把輸入向量用一個 embedding 層降維策劃那個稠密連續的向量，如本文介紹的用 FM 去做預訓練，或者和模型一起聯合訓練，或者其他資料源提取的 embedding 特徵向量去做 concat。

其次，在寬和深的大戰中，在 Google 提出了 Wide & Deep 模型框架後，這套體系基本已成為業內的基本框架。無論 Wide 部分或者 Deep 怎麼改造，其實本質上還是一些常見元件的結合，或者改造 Wide，或者改造 Weep，或者在 Wide 和 Deep 的結合過程中進行改造。 

CTR 預估領域方法變化層出不窮，但萬變不離其宗，各種模型本質上還是基礎元件的組合，如何結合自己的業務、資料、應用場景去挑選合適的模型應用，可能才是真正的難點所在。

參考文獻

[1] Factorization Machines 

[2] Wide & Deep Learning for Recommender Systems 

[3] Deep Learning over Multi-Field Categorical Data: A Case Study on User Response Prediction 

[4] Product-based Neural Networks for User Response Prediction 

[5] DeepFM: A Factorization-Machine based Neural Network for CTR Prediction 

[6] Neural Factorization Machines for Sparse Predictive Analytics 

[7] Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks 

[8] Deep & Cross Network for Ad Click Predictions 

[9] Deep Interest Network for Click-Through Rate Prediction

#作 者 招 募#




讓你的文字被很多很多人看到，喜歡我們不如加入我們




          

 我是彩蛋

 解鎖新功能：熱門職位推薦！

PaperWeekly小程式升級啦

今日arXiv√猜你喜歡√熱門職位√

找全職找實習都不是問題

 

 解鎖方式 

1. 識別下方二維碼開啟小程式

2. 用PaperWeekly社群賬號進行登陸

3. 登陸後即可解鎖所有功能

 職位釋出 

請新增小助手微信（pwbot02）進行諮詢

 


長按識別二維碼，使用小程式

賬號註冊paperweek.ly



關於PaperWeekly





PaperWeekly 是一個推薦、解讀、討論、報道人工智慧前沿論文成果的學術平臺。如果你研究或從事 AI 領域，歡迎在公眾號後臺點選「交流群」，小助手將把你帶入 PaperWeekly 的交流群裡。



▽ 點選 | 閱讀原文 | 進入作者知乎專欄