知識星球作者丨蘇劍林
單位丨廣州火焰資訊科技有限公司
研究方向丨NLP，神經網路
個人主頁丨kexue.fm
話說我覺得我自己最近寫文章都喜歡長篇大論了，而且扎堆地來。之前連續寫了三篇關於 Capsule 的介紹，這次輪到 VAE 了。本文是 VAE 的第三篇探索，說不準還會有第四篇。不管怎麼樣，數量不重要，重要的是能把問題都想清楚。尤其是對於 VAE 這種新奇的建模思維來說，更加值得細細地摳。
這次我們要關心的一個問題是：VAE 為什麼能成？
估計看 VAE 的讀者都會經歷這麼幾個階段。第一個階段是剛讀了 VAE 的介紹，然後雲裡霧裡的，感覺像自編碼器又不像自編碼器的，反覆啃了幾遍文字並看了原始碼之後才知道大概是怎麼回事。
第二個階段就是在第一個階段的基礎上，再去細讀 VAE 的原理，諸如隱變數模型、KL 散度、變分推斷等等，細細看下去，發現雖然折騰來折騰去，最終居然都能看明白了。
這時候讀者可能就進入第三個階段了。在這個階段中，我們會有諸多疑問，尤其是可行性的疑問：“為什麼它這樣反覆折騰，最終出來模型是可行的？我也有很多想法呀，為什麼我的想法就不行？”
前文之要
讓我們再不厭其煩地回顧一下前面關於 VAE 的一些原理。
VAE 希望透過隱變數分解來描述資料 X 的分佈。
然後對 p(x,z) 用模型 q(x|z) 擬合，p(z) 用模型 q(z) 擬合，為了使得模型具有生成能力，q(z) 定義為標準正態分佈。
理論上，我們可以使用邊緣機率的最大似然來求解模型：
但是由於圓括號內的積分沒法顯式求出來，所以我們只好引入 KL 散度來觀察聯合分佈的差距，最終標的函式變成了：
透過最小化 L 來分別找出 p(x|z) 和 q(x|z)。前一文再談變分自編碼器VAE：從貝葉斯觀點出發也表明 L 有下界 −?x∼p(x)[lnp(x)]，所以比較 L 與 −?x∼p(x)[lnp(x)] 的接近程度就可以比較生成器的相對質量。
取樣之惑
在這部分內容中，我們試圖對 VAE 的原理做細緻的追問，以求能回答 VAE 為什麼這樣做，最關鍵的問題是，為什麼這樣做就可行。
取樣一個點就夠
對於 (3) 式，我們後面是這樣處理的：
1. 留意到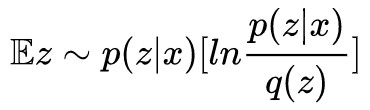
正好是 p(z|x) 和 q(z) 的散度 KL(p(z|x)‖q(z))，而它們倆都被我們都假設為正態分佈，所以這一項可以算出來；
2. ?z∼p(z|x)[−lnq(x|z)] 這一項我們認為只取樣一個就夠代表性了，所以這一項變成了 −lnq(x|z),z∼p(z|x)。
經過這樣的處理，整個 loss 就可以明確寫出來了：
等等，可能有讀者看不過眼了：KL(p(z|x)‖q(z)) 事先算出來，相當於是取樣了無窮多個點來估算這一項；而 ?z∼p(z|x)[−lnq(x|z)] 卻又只取樣一個點，大家都是 loss 的一部分，這樣不公平待遇真的好麼？
事實上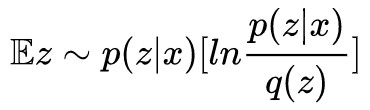，也可以只取樣一個點來算，也就是說，可以透過全體都只取樣一個點，將 (3) 式變為：
這個 loss 雖然跟標準的 VAE 有所不同，但事實上也能收斂到相似的結果。
為什麼一個點就夠？
那麼，為什麼取樣一個點就夠了呢？什麼情況下才是取樣一個點就夠？
首先，我舉一個“取樣一個點不夠”的例子，讓我們回頭看 (2) 式，它其實可以改寫成：
如果取樣一個點就夠了，不，這裡還是謹慎一點，取樣 k 個點吧，那麼我們可以寫出：
然後就可以梯度下降訓練了。
然而，這樣的策略是不成功的。實際中我們能取樣的數目 k，一般要比每個 batch 的大小要小，這時候最大化
就會陷入一個“資源爭奪戰”的境地。
每次迭代時，一個 batch 中的各個 xi 都在爭奪 z1,z2,…,zk，誰爭奪成功了，q(x|z) 就大。說白了，哪個 xi 能找到專屬於它的 zj，這意味著 zj 只能生成 xi，不能生成其它的，那麼 z(xi|zj) 就大），但是每個樣本都是平等的，取樣又是隨機的，我們無法預估每次“資源爭奪戰”的戰況。這完全就是一片混戰。
如果資料集僅僅是 mnist，那還好一點，因為 mnist 的樣本具有比較明顯的聚類傾向，所以取樣數母 k 超過 10，那麼就夠各個 xi 分了。
但如果像人臉、imagenet 這些沒有明顯聚類傾向、類內方差比較大的資料集，各個 z 完全是不夠分的，一會 xi 搶到了 zj，一會 xi+1 搶到了 zj，訓練就直接失敗了。
因此，正是這種“僧多粥少”的情況導致上述模型 (7) 訓練不成功。可是，為什麼 VAE 那裡取樣一個點就成功了呢？
一個點確實夠了
這就得再分析一下我們對 q(x|z) 的想法了，我們稱 q(x|z) 為生成模型部分，一般情況下我們假設它為伯努利分佈或高斯分佈，考慮到伯努利分佈應用場景有限，這裡只假設它是正態分佈，那麼：
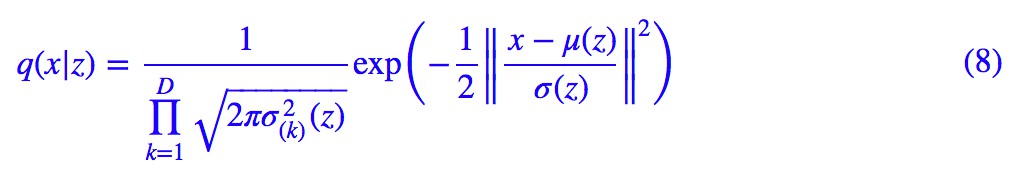
其中 μ(z) 是用來計算均值的網路，σ^2(z)是用來計算方差的網路，很多時候我們會固定方差，那就只剩一個計算均值的網路了。
註意，q(x|z) 只是一個機率分佈，我們從q(z)中取樣出 z 後，代入 q(x|z) 後得到 q(x|z) 的具體形式，理論上我們還要從 q(x|z) 中再取樣一次才得到 x。但是，我們並沒有這樣做，我們直接把均值網路 μ(z) 的結果就當成 x。
而能這樣做，表明 q(x|z) 是一個方差很小的正態分佈（如果是固定方差的話，則訓練前需要調低方差，如果不是正態分佈而是伯努利分佈的話，則不需要考慮這個問題，它只有一組引數），每次取樣的結果幾乎都是相同的（都是均值 μ(z)），此時 x 和 z 之間“幾乎”具有一一對應關係，接近確定的函式 x=μ(z)。
▲ 標準正態分佈（藍）和小方差正態分佈（橙）
而對於後驗分佈 p(z|x) 中，我們假設了它也是一個正態分佈。既然前面說 z 與 x 幾乎是一一對應的，那麼這個性質同樣也適用驗分佈 p(z|x)，這就表明後驗分佈也會是一個方差很小的正態分佈（讀者也可以自行從 mnist 的 encoder 結果來驗證這一點），這也就意味著每次從 p(z|x) 中取樣的結果幾乎都是相同的。
既然如此，取樣一次跟取樣多次也就沒有什麼差別了，因為每次取樣的結果都基本一樣。所以我們就解釋了為什麼可以從 (3) 式出發，只取樣一個點計算而變成 (4) 式或 (5) 式了。
後驗之妙
前面我們初步解釋了為什麼直接在先驗分佈 q(z) 中取樣訓練不好，而在後驗分佈中 p(z|x) 中取樣的話一個點就夠了。
事實上，利用 KL 散度在隱變數模型中引入後驗分佈是一個非常神奇的招數。在這部分內容中，我們再整理一下相關內容，並且給出一個運用這個思想的新例子。
後驗的先驗
可能讀者會有點邏輯混亂：你說 q(x|z) 和 p(z|x) 最終都是方差很小的正態分佈，可那是最終的訓練結果而已，在建模的時候，理論上我們不能事先知道 q(x|z) 和 p(z|x) 的方差有多大，那怎麼就先去取樣一個點了？
我覺得這也是我們對問題的先驗認識。當我們決定用某個資料集 X 做 VAE 時，這個資料集本身就帶了很強的約束。
比如 mnist 資料集具有 784 個畫素，事實上它的獨立維度遠少於 784，最明顯的，有些邊緣畫素一直都是 0，mnist 相對於所有 28*28 的影象來說，是一個非常小的子集.
再比如筆者前幾天寫的作詩機器人，“唐詩”這個語料集相對於一般的陳述句來說是一個非常小的子集；甚至我們拿上千個分類的 imagenet 資料集來看，它也是無窮盡的影象中的一個小子集而已。
這樣一來，我們就想著這個資料集 X 是可以投影到一個低維空間（隱變數空間）中，然後讓低維空間中的隱變數跟原來的 X 集一一對應。
讀者或許看出來了：這不就是普通的自編碼器嗎？
是的，其實意思就是說，在普通的自編碼器情況下，我們可以做到隱變數跟原資料集的一一對應（完全一一對應意味著 p(z|x) 和 q(x|z) 的方差為 0），那麼再引入高斯形式的先驗分佈 q(z) 後，粗略地看，這隻是對隱變數空間做了平移和縮放，所以方差也可以不大。
所以，我們應該是事先猜測出 p(z|x) 和 q(x|z) 的方差很小，並且讓模型實現這個估計。說白了，“取樣一個”這個操作，是我們對資料和模型的先驗認識，是對後驗分佈的先驗，並且我們透過這個先驗認識來希望模型能靠近這個先驗認識去。
整個思路應該是：
-
有了原始語料集
-
觀察原始語料集，推測可以一一對應某個隱變數空間
-
透過取樣一個的方式，讓模型去學會這個對應
這部分內容說得有點凌亂，其實也有種多此一舉的感覺，希望讀者不要被我搞糊塗了。如果覺得混亂的話，忽視這部分吧。
耿直的IWAE
接下來的例子稱為“重要性加權自編碼器（Importance Weighted Autoencoders）”，簡寫為“IWAE”，它更加乾脆、直接地體現出後驗分佈的妙用，它在某種程度上它還可以看成是 VAE 的升級版。
IWAE 的出發點是 (2) 式，它引入了後驗分佈對 (2) 式進行了改寫：
這樣一來，問題由從 q(z) 取樣變成了從 p(z|x) 中取樣。我們前面已經論述了 p(z|x) 方差較小，因此取樣幾個點就夠了：
代入 (2) 式得到：
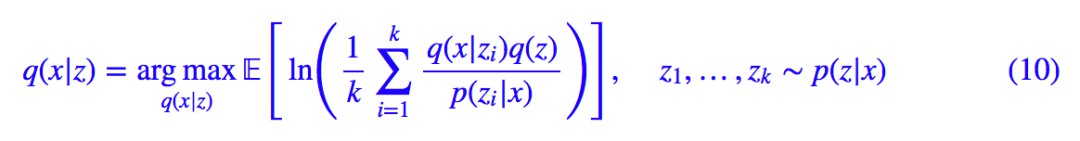
這就是 IWAE。為了對齊 (4),(5) 式，可以將它等價地寫成：
當 k=1 時，上式正好跟 (5) 式一樣，所以從這個角度來看，IWAE 是 VAE 的升級版。
從構造過程來看，在 (8) 式中將 p(z|x) 替換為 z 的任意分佈都是可以的，選擇 p(z|x) 只是因為它有聚焦性，便於取樣。而當 k 足夠大時，事實上 p(z|x) 的具體形式已經不重要了。
這也就表明，在 IWAE 中削弱了 encoder 模型 p(z|x) 的作用，換來了生成模型 q(x|z) 的提升。
因為在 VAE 中，我們假設 p(z|x) 是正態分佈，這隻是一種容易算的近似，這個近似的合理性，同時也會影響生成模型 q(x|z) 的質量。可以證明，Lk能比 L 更接近下界 −?x∼p(x)[lnp(x)]，所以生成模型的質量會更優。
直覺來講，就是在 IWAE 中，p(z|x) 的近似程度已經不是那麼重要了，所以能得到更好的生成模型。
不過代價是生成模型的質量就降低了，這也是因為 p(z|x) 的重要性降低了，模型就不會太集中精力訓練 p(z|x) 了。所以如果我們是希望獲得好的 encoder 的話，IWAE 是不可取的。
還有一個工作 Tighter Variational Bounds are Not Necessarily Better，據說同時了提高了 encoder 和 decoder 的質量，不過我還沒看懂。
重參之神
如果說後驗分佈的引入成功勾畫了 VAE 的整個藍圖，那麼重引數技巧就是那“畫龍點睛”的“神來之筆”。
前面我們說，VAE 引入後驗分佈使得取樣從寬鬆的標準正態分佈 q(z) 轉移到了緊湊的正態分佈 p(z|x)。然而，儘管它們都是正態分佈，但是含義卻大不一樣。我們先寫出：
也就是說，p(z|x) 的均值和方差都是要訓練的模型。
讓我們想象一下，當模型跑到這一步，然後算出了 μ(x) 和 σ(x)，接著呢，就可以構建正態分佈然後取樣了。
可取樣出來的是什麼東西？是一個向量，並且這個向量我們看不出它跟 μ(x) 和 σ(x) 的關係，所以相當於一個常向量，這個向量一求導就沒了，從而在梯度下降中，我們無法得到任何反饋來更新 μ(x) 和 σ(x)。
這時候重引數技巧就閃亮登場了，它直截了當地告訴我們：
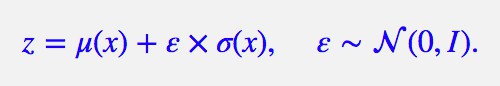
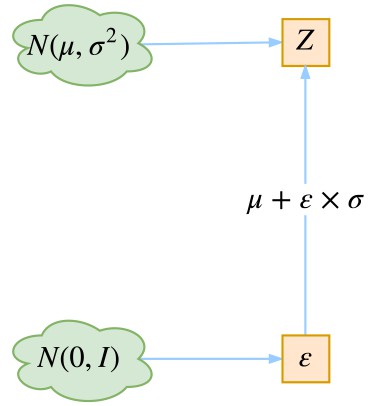
▲ 重引數技巧
沒有比這更簡潔了，看起來只是一個微小的變換，但它明確地告訴了我們 z 跟 μ(x) 和 σ(x) 的關係。於是 z 求導就不再是 0，μ(x), σ(x) 終於可以獲得屬於它們的反饋了。至此，模型一切就緒，接下來就是寫程式碼的時間了。
可見，“重引數”簡直堪稱絕殺。
本文之水
本文大概是希望把 VAE 後續的一些小細節說清楚，特別是 VAE 如何透過巧妙地引入後驗分佈來解決取樣難題（從而解決了訓練難題），並且順道介紹了一下 IWAE。
要求直觀理解就難免會失去一點嚴謹性，這是二者不可兼得的事情。所以，對於文章中的毛病，望高手讀者多多海涵，也歡迎批評建議。
點選以下標題檢視相關內容：
#作 者 招 募#
我是彩蛋
解鎖新功能：熱門職位推薦！
PaperWeekly小程式升級啦
今日arXiv√猜你喜歡√熱門職位√
找全職找實習都不是問題
解鎖方式
1. 識別下方二維碼開啟小程式
2. 用PaperWeekly社群賬號進行登陸
3. 登陸後即可解鎖所有功能
職位釋出
請新增小助手微信（pwbot02）進行諮詢
長按識別二維碼，使用小程式
*點選閱讀原文即可註冊
關於PaperWeekly
PaperWeekly 是一個推薦、解讀、討論、報道人工智慧前沿論文成果的學術平臺。如果你研究或從事 AI 領域，歡迎在公眾號後臺點選「交流群」，小助手將把你帶入 PaperWeekly 的交流群裡。
▽ 點選 | 閱讀原文 | 進入作者部落格