如何優雅地測量一隻貓的體積？

前情提要：

Monte Carlo 測貓法：

把貓裝進已知體積為V_box的盒子，在盒子內均勻取N個隨機點，其中M個在貓體內，貓體積近似為V_box*M/N。推理及討論見後面的supplemental materials.

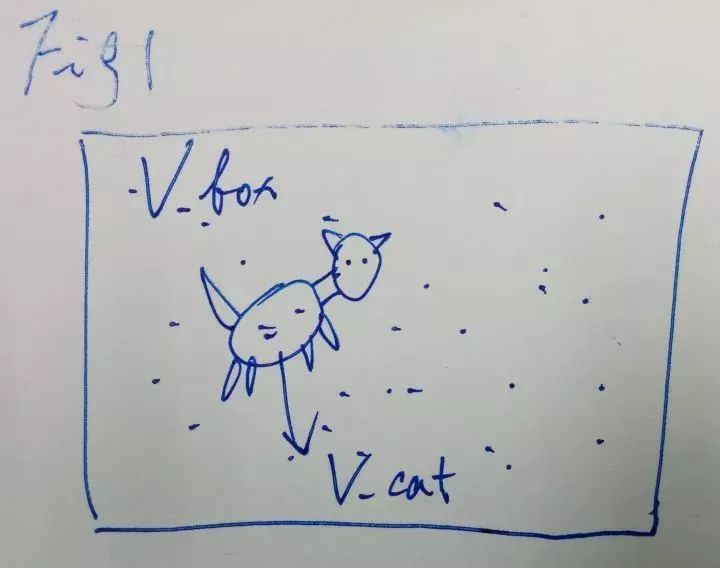
要實現這一測貓法，需要一種瞬時確定某點是貓還是非貓的方法，否則在貓運動的情況下，會測得貓掃過的體積而不是貓體積。

我決定用下圖所示的方法。。。

盒子壁上裝儘量多的鐳射燈，盒子壁用感光材料。若要確定某點是貓還是非貓，則讓所有鐳射燈射向標的點。若標的點是貓，則鐳射會被貓擋住因此盒子壁上任何一點都不會檢測到鐳射。因此我們用以下原則判斷標的點是貓非貓：

• 若有盒子壁上任何一點檢測到鐳射，說明標的點非貓。
  

• 否則認為該點是貓。

測量可以在很短的時間內完成，足以快到忽略貓的運動。

============
當然這種方法是有缺陷的，貓身上一些凹陷部位可能會成為鐳射無法穿過的死角，因此被算入貓體積。

一個充分不必要的解決方法是讓貓變成凸貓(convex cat), 即任取兩點屬於貓，兩點之間的線段上的點都屬於貓，滿足這一條件的貓叫做凸貓，如下圖所示。

下圖是一個現實生活中凸貓的例子。。（圖片來自網路）

對於凸貓，該方法測得的貓體積即為真貓體積，證明見supplemental materials中的夾逼測貓法。

但是這種方法是不貓道的，因為貓咪宣言中有這樣的話：

We hold these truths to be self-evident, that all cats are created equal （大霧）, and they are endowed by their Creator with certain unalienable rights, that among these are the rights to stand up, lie down, turn around, groom themselves and stretch their limbs …

而凸貓顯然（至少）剝奪了貓咪 stretch their limbs 的自由。。。

好在對於非凸貓，該方法也不是那麼糟糕。

下麵我將展示給大家，即使對於非凸貓，用該方法測出來的貓體積

• 首先本身就是一種很合理的貓體積定義

• 其次實際操作中與一般意義上的貓體積差別不大
  

=============

要測量貓體積，首先要定義貓體積。

然而“貓有毛兮毛有枝，本喵在哪你不知。”

貓的體積定義並非顯而易見的，主要有兩個困難：

1. 貓的錶面是凹凸不平的，那些凹陷和縫隙怎麼算？客觀標準是什麼呢？

2. 喵是測不準的。理論上來講喵的電子雲可以想你時你在天邊，想你時你在眼前，哪裡算邊界？

嗯。。化學家出場了。。。

化學家測貓大法：

把一個直徑一定的毛線球用一定力量按在喵體表滾一遍，把毛線球與喵接觸的內錶面軌跡包括的空間的體積視為貓的體積，並稱之為Van de Waals cat volume .（好吧。。。我知道這不叫Van de Waals體積。。但是這個體積的實際名字土掉渣了。。哪有Van de Waals高大上。。。）

如下圖。

這一體積定義包含兩個要素。毛線球的直徑和按在貓身上的力量，前者決定了凹陷和縫隙算與不算的體積和形狀標準——毛線球放得進就算，否則不算；後者決定了貓邊界的標準——和毛線球之間的作用力達到某一值為準，啥啥電子雲都不好使，就看力的大小。透過改變毛線球和力量的大小，可以控制貓體積的精細程度。究竟多精細不重要，重要的是可以定義一個體積的客觀標準。

=============
仿照這一定義，我將我測得的貓體積定義為 Van de Bars cat volume。。。如下圖。。。

準確來說，是一個直徑相當於鐳射束粗度，無限長的bar在貓錶面滾過定義的貓體積。。。你看。。。我測的體積也是有一個很有道理的定義的嘛。。。。

同時我想強調，相對於其他回答，該方法對貓毛可以有很嚴格的處理，詳見supplemental materials中對貓毛的討論。

============

我認為實際測量中Van de Bars 貓體積和我們一般認為的貓體積差異並不大。

比如看下圖

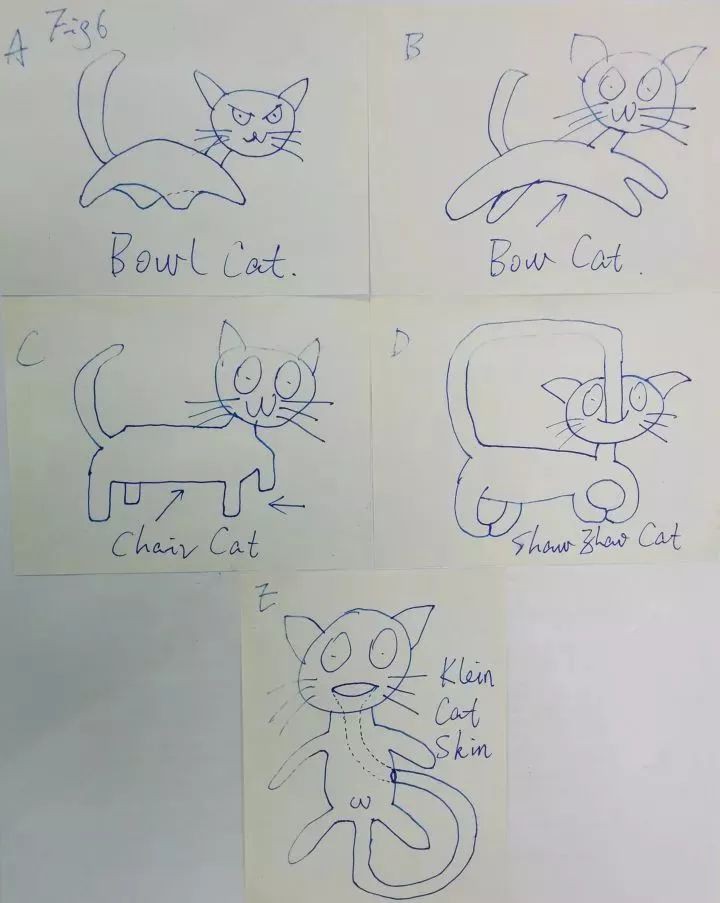
E為克萊因貓，虛線部分在貓體內。。

對於碗狀貓(bowl cat)，Van de Bars 貓體積確實會把貓肚子下麵那塊空間誤算做貓體積的一部分。但是對弓狀貓(bow cat)、椅狀貓(chair cat)的測量都是準確的，因為光線可以從圖上箭頭的角度穿過。甚至小昭貓(shaw zhao cat)這個我本來覺得挺奇葩的形狀下其實並沒有任何問題。這樣一來，Van de Bars 貓體積在多數情況下和我們一般認為的貓體積的區別也就僅限於耳廓內的空間、個別身體縫隙之類的光穿不過的死角。。。我覺得還是能接受的。。。

為了儘量避免碗狀貓對測量的影響，我們要大力鼓勵貓咪充分 stretch their limbs. 這也提示我們，愛護貓咪對我們藍星人也是有益的。。。所以愛護貓咪，人人有責，no cats should be convex!!!

=============

綜上，我設計了一種測量Van de Bars 貓體積的Monte Carlo測貓法。我覺得這是目前回答裡最貓道最優雅的。。。因為它保障了貓咪伸展身體、弄乾身體、不受恐嚇、自由站起、躺下、翻身的權利。。。而且對貓體積有嚴謹而實用的定義。。。

==============

Supplemental materials:

• Monte carlo 測貓法的推理：
  

把貓裝進體積為V的盒子，在盒子內 uniform randomly 取N個 independent and identically distributed (i.i.d.) 的點組成樣本，記為 SAMPLE = {(xi, yi, zi) | i in range(0, N)}。

定義如下 function：
I(x, y, z) = 1 if (x, y, z) in CAT else 0
（即確定一個點是貓還是非貓）

假設貓體積(V_cat)不變，且貓的運動與取點不相關（即貓既不接飛鏢也不躲飛鏢，見評論區知友討論），則I(x, y, z)具有如下分佈：

I(x, y, z) = 0 with a probability of 1-V_cat/V_box
I(x, y, z) = 1 with a probability of V_cat/V_box

與貓運動與否不相關。

根據這一分佈I(x, y, z)的期望值是V_cat/V_box.
{I(xi, yi, zi) | (xi, yi, zi) in SAMPLE} 是一個服從上述分佈的 i.i.d. 的sample。

根據大數定理(law of large numbers), sample mean almost surely converges to expected value. 所以可以用 sample mean 估計期望值，即：
V_cat/V_box ～= sum(I(xi, yi, zi))/N

記M為在貓體內的樣本點數量，則
V_cat/V_box ～= sum(I(xi, yi, zi))/N = M/N

所以V_cat ~= V_box * M/N

關於貓毛的討論

上述方法等價於把貓邊界定義為貓體表透光率顯著不同於空氣以至於足以使得sensor檢測到差異的位置。可以想象這應該包括了貓毛，而且是不受壓迫不變形的貓毛。

我認為這也是該方法的一大優勢——這是真正的無損測真貓，而不是測 a rat-like creature that lives inside a cat （見 @蒼原雪在本問題下的回答）。。。其他方法，包括彩虹糖，都是有壓迫的。實際上彩虹糖法測的是彩虹糖的形狀和大小、彩虹糖與貓接觸處的壓強定義的Van de Waals cat volume. 因為這一壓強，長毛貓的測量可能和我們預想的含貓毛體積有較大區別。

Van de Bars 貓體積和其他貓體積的對比 （不適用於克萊因貓）

• VS 真 貓體積

• 這裡真貓體積指刨除一切空隙的貓體積。顯然，Van de Bars 貓體積 >= 真貓體積。所以Van de Bars 貓體積是真貓體積的一個upper bound. 可惜的是它們之間的差是沒有任何保證的，比如口袋貓。

• VS Van de 毛線球 貓體積

• 我覺得Van de Bars 貓體積應該是與bar同樣直徑的毛線球定義出的Van de 毛線球貓體積的upper bound，但是我沒仔細證。。。因為比如bowl cat這樣的存在，它們的差同樣是沒upper limit的。。。

• VS Convex Hull （附夾逼測貓法）

• 一個set的convex hull 是包含這個set且convex的最小的set。如圖3和下圖。

• 易知Convex hull 貓體積 >= Van de Bars 貓體積 >= Van de 毛線球貓體積 >= 真貓體積。對於convex貓，因為貓本身就是convex的，所以貓和貓的convex hull是同一集合，所以Convex hull貓體積 = 真貓體積，所以convex cat 的真體積 = Van de 毛線球體積 = Van de Bars體積 = Convex hull 體積。。。。。。夾逼測貓法。。。。convex 貓真好測。。。各種體積都一樣。。。all cats should be convex。。。

• 關於克萊因貓

• 準確講克萊因貓應該是克萊因貓皮(Klein Cat Skin)，因為這是一個曲面而不是物體，而且這個曲面不能把空間分為內、外互不連通的兩部分，所以也無法把克萊因貓體積定義為克萊因貓皮圍成的空間的體積。仔細看Fig. 6 E 的話，克萊因貓“體內”的空間可以透過尾巴－食道－口和外界相通。所以嚴格講，克萊因貓無體積。

• 但是這並不妨礙我們繼續強測克萊因貓的 Van de 毛線球體積和 Van de Bars 體積，只是不同於之前可以把這作為真貓體積的近似，現在我們必須將其作為一種獨立的體積定義使用。

• 在克萊因貓上 Van de Bars 貓體積比 Van de 毛線球貓體積魯棒。因為當毛線球小到克萊因貓可以吞下去的時候，毛線球會沿著口－食道－尾巴通路把喵“體內”滾個遍，然後 Van de 毛線球體積為零。。。而 Van de Bars 體積因為使用的是無限長的bar, 所以即使bar直徑再小也無法access喵“體內”的空間。這允許我們用較細的bar來提高測量準確度而不必擔心體積忽然降為0.

=========下麵是原答案===============

物理學家測貓法：取一隻半徑為r的真空中的球形貓，體積等於4/3*πr^3

數學家測貓法：把貓裝進已知體積為V的盒子，在盒子內均勻取N個隨機點，其中M個在貓體內，貓體積近似為VM/N。

生物學家測貓法：把control貓裝盒子，塞了10次都塞進去了，把實驗貓裝同一個盒子，塞了10次只進去兩次，所以，貓多大我不知道，反正顯著大於control貓。

資料來源於有勇有萌兔（知乎）： https://www.zhihu.com/question/36590161/answer/68200338