(點選上方公眾號,可快速關註)
來源:沙漠之鷹 ,
www.cnblogs.com/buptzym/p/8677482.html
營銷是發現或挖掘準消費者和眾多商家需求,透過對自身商品和服務的最佳化和定製,進而推廣、傳播和銷售產品,實現最大化利益的過程。例如,銀行可透過免息卡或降價對處在分期意願邊緣的使用者進行營銷,促使其分期進而提升整體利潤;選擇最優時機和地點對使用者進行廣告投放提升轉化。
在大資料和“千人千面”的背景下,營銷升級為“精準營銷”,對每個使用者的需求進行更加精細的個性化分析與投放,進而實現使用者滿意,廣告主和平臺獲益的多贏局面。營銷演演算法的步驟一般為:1) 圈人,2) 召回和排序 3) 在預算約束下,透過最大化ROI或利潤uplift確定最終策略。
營銷演演算法與傳統的推薦召回的評估方法不盡相同,推薦召回等可透過CTR,準確率,AUC等方式進行評估。但營銷的評估會更複雜,有以下四方面的難題:
1) 要以提升整體利潤和使用者滿意度為標的,甚至還要考慮長遠收益,不是簡單的二分類或回歸問題
2) 營銷通常包含有多種決策,且比推薦更複雜的策略流程,其最終效果取決於策略和整體流程的最最佳化
3) 營銷一般有預算限制,並要考慮投入產出比
4) 根本原因是:相比於分類等問題,知道當前決策對於任何個體是否是最優的幾乎是不可能的,因為其響應在特定決策下是不可觀測的。例如發放免息券,我們只能對某個個體在單一時間發放某一類特定的免息券,但無法在事先就知道這種決策就是最優的。重覆實驗在個體上是不可能實現的。因此,即使是從隨機試驗中獲取的資料,在機率視角上也是unlabeled,因為即使在訓練集上,在最優決策下試圖預測的真實值(如響應率等)都是未知的。
由於成本原因,不可能做大量的隨機實驗。然而在做A/B test時,依然需要類似AUC等明確且容易解釋的業務指標來評估營銷演演算法模型好壞。但是,是否有較準確的評估營銷演演算法效能的方法?
在此背景下,我們實現了multiple treatment(多決策評估)演演算法,其思路來自於論文《Uplift Modeling with Multiple Treatments and General Response Types》,該演演算法實現簡單,理論完備,具有類似AUC一樣優良的直觀和可對比性。同時model-free,與具體所用的演演算法和策略無關。
我們會給出其容易理解的業務解釋,補充其使用必要條件,完善理論推導。
多treatment的簡單圖例說明
我們先給出最簡單的一個營銷方案,來圖示講解該演演算法的原理。
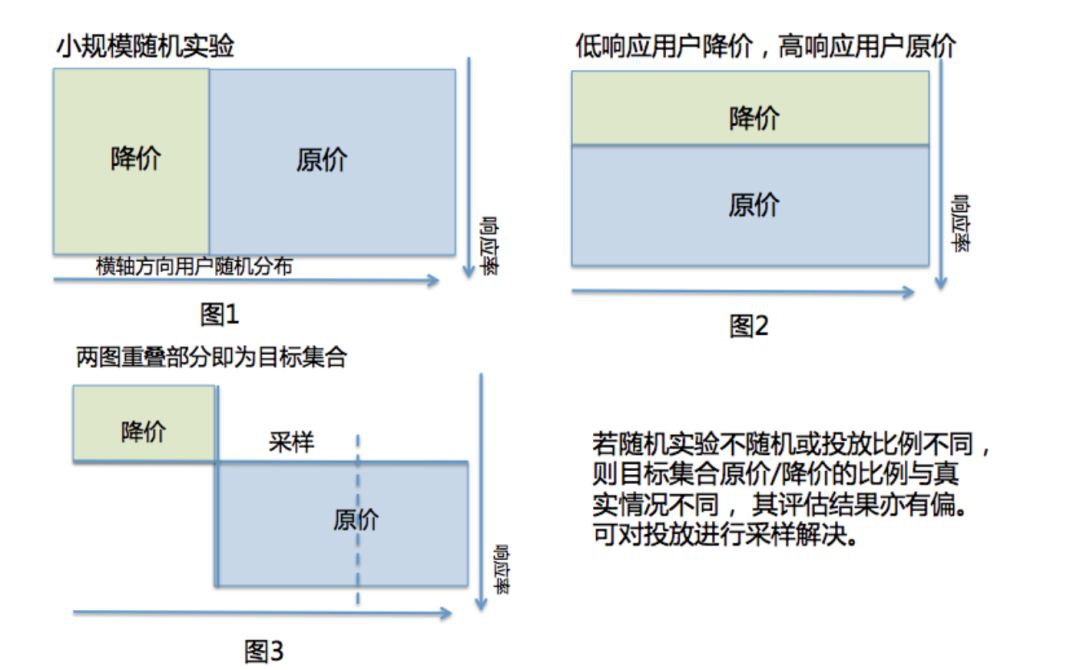
對所有使用者,有兩種策略:原價/降價,在進行演演算法實驗前,先進行了一輪小流量隨機投放實驗,兩種策略投放比例各佔50%。我們提出一種最簡單的閾值策略:“低響應使用者降價,高響應使用者原價”,之後需要評估該策略的線上利潤率。

如上圖所示,縱軸為響應率軸,橫軸為隨機軸。隨機實驗與策略有兩塊重疊部分,即圖3。由於重疊部分是歷史已知可觀測的,因此評估其重疊部分的利潤率,即可代表整體策略的利潤率。
仔細思考整個方法,思路非常簡單,即使用無偏的部分樣本的特性和統計量去代表整體,這幾乎是初中數學的知識。只要樣本足夠多,其歷史回測完全可以接近真實線上的效果。
該方法雖然想法很樸素,但必須註意一些很容易被忽略的條件:
1) 隨機樣本的數量即各塊的面積要足夠大,從而避免異常或特殊樣本對整體評估效果的影響。
2) 隨機實驗必須隨機且不同treatment的投放比例需一致,但真實投放時各treatment不需平均分配。下圖解釋了其原因:
3) 各treatment需要離散且數量遠小於樣本數,且各自獨立(不過很難想象各treatment之間不獨立的情形)
4) 需要使用最近的歷史資料才能相對準確,要求環境必須有一定的平穩性,否則基於歷史資料的回測就沒有了意義。
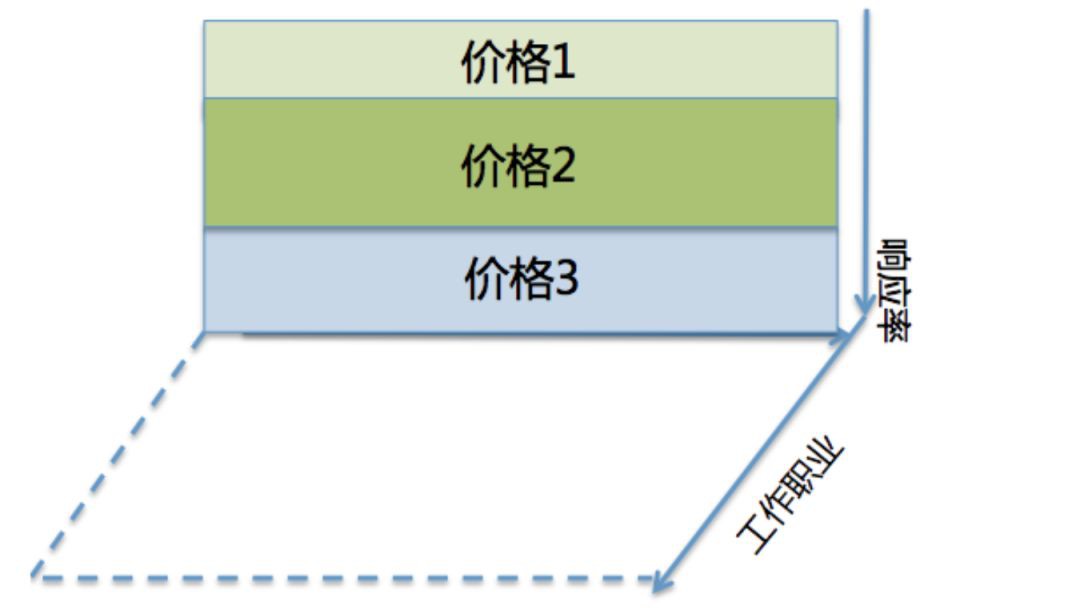
再將其擴充套件為的多種treatment的複雜情形。若針對響應率進行多分段決策,則不需證明就能保證各決策在圖中一定是直線且互相平行,與隨機軸正交(否則策略就有猜測隨機的能力),如下圖所示:

若策略不僅需要考慮響應率,還需考慮其他指標如職業,則可以增加一條坐標軸代表職業,也一定與隨機軸正交,構成高維線性空間,命中部分變為空間中的小區塊,對區塊的彙總依然能代表整體策略的利潤率。值得註意的是,職業不一定需要需要響應率正交。
理論推導
一個uplift模型將整個特徵空間分割為多個子空間,每個空間代表一種策略。在隨機試驗中,是能夠獲取一個樣本隨機落入某個子空間(即命中)的機率和其對應的響應的。因此透過計算整體命中子空間的響應,就能獲取整體特徵空間的真實響應。
在隨機實驗中,令K為所有可能的treatment數量,令pt代表一個treatment等於t的機率,在任何有意義的場合,都能保證pt>0 for t=0,…K
下麵的論文截圖給出了一個引理:

對一組隨機實驗資料sN=(x(i),t(i),y(i),i=1,2,…,N), 計算】z(i)是很容易的。如果ith個樣本正好匹配了真實的treatment,則z(i)=y(i)/pt, 即真實響應會被該treatment的機率所縮放,否則z(i)總為0。 由於對樣本的平均就是對期望值的無偏估計,因此我們有如下的概念:

進一步地,可以計算z均值的置信區間,來幫助我們估計E[Y|T]=h(X)]的置信度。 此處可以參考顯著性檢驗的相關文章(如這篇)
如何對長期收益進行計算和建模?
雖然思路簡單,易於實現,多treatment評估也只能解決短期決策評估,但使用者和環境是時變的,當使用者接受多個treatment(如降價獎勵,紅包或提價)之後,心智會發生改變,短期最大化收益不代表長期收益。
假設某一種策略被實施多次,我們已經能夠觀察到單個使用者/群體的長程treatment和response,如何使用強化學習對時序資訊進行建模?如何準確有效地對長程收益進行評估?這些都是非常有趣的問題。
看完本文有收穫?請轉發分享給更多人
關註「ImportNew」,提升Java技能

 知識星球
知識星球