關於作者：麥振生，中山大學資料科學與計算機學院碩士生，研究方向為自然語言處理和問答系統。

■ 論文 | Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN

■ 連結 | https://www.paperweekly.site/papers/1757

■ 原始碼 | https://github.com/batzner/indrnn

論文亮點

傳統 RNN 因為在時間上引數共享，所以會出現梯度消失/爆炸問題。LSTM/GRU 在解決層內梯度消失/爆炸問題時，梯度仍然會在層間衰減，所以 LSTM/GRU 難以做成多層網路。並且，LSTM/GRU 也存在著無法捕捉更長的時序資訊的問題。

此外，傳統 RNN 由於層內神經元相互聯絡，難以對神經元的行為進行合理的解釋。

基於上述問題，論文提出了 IndRNN，亮點在於：

1. 將 RNN 層內神經元解耦，使它們相互獨立，提高神經元的可解釋性。

2. 有序串列能夠使用 Relu 等非飽和啟用函式，解決層內和層間梯度消失/爆炸問題，同時模型也具有魯棒性。

3. 有序串列比 LSTM 能處理更長的序列資訊。

模型介紹

論文模型比較簡單。介紹模型前，我們先來理一下 RNN 梯度的有關知識。

RNN梯度問題

先來看 RNN 隱狀態的計算：

設 T 時刻的標的函式為 J，則反向傳播時到 t 時刻的梯度計算：

其中 diag(σ′(hk+1) 是啟用函式的雅可比矩陣。可以看到，RNN 的梯度計算依賴於對角矩陣 diag(σ′(hk+1))U^T 的連積，即求該對角陣的 n 次冪。

• 對角元素只要有一個小於 1，那麼 n 次乘積後會趨近於 0；

• 對角元素只要有一個大於 1，那麼 n 次乘積後會趨近無窮大。

RNN 常用的兩種啟用函式，tanh 的導數為 1−tanh2 ，最大值為 1，影象兩端趨於 0；sigmoid 的導數為 sigmoid(1−sigmoid) ，最大值為 0.25，影象兩端趨於 0。

可見兩種啟用函式的導數取值絕大部分小於 1。因此它們與迴圈權重繫數相乘構成的對角矩陣元素絕大部分小於 1（可能會有等於 1 的情況，但不會大於 1），連積操作會導致梯度指數級下降，即“梯度消失”現象。對應第一種情況。 

而在 RNN 中使用 Relu 函式，由於 Relu 在 x>0 時導數恆為 1，因此若 U 中元素有大於 1 的，則構成的對角矩陣會有大於 1 的元素，連積操作會造成梯度爆炸現象。對應第二種情況。

解決方案

門控函式（LSTM/GRU）

引入門控的目的在於將啟用函式導數的連乘變成加法。以 LSTM 為例：

反向傳播時有兩個隱態：

其中僅 C(t) 參與反向傳播：

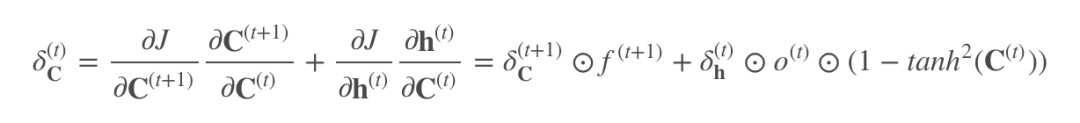
加號後的項就是 tanh 的導數，這裡起作用的是加號前的項， f(t+1) 控制著梯度衰減的程度。當 f=1 時，即使後面的項很小，梯度仍能很好地傳到上一時刻；f=0 時，即上一時刻的訊號對此刻不造成任何影響，因此可以為 0。 

門控函式雖然有效緩解了梯度消失的問題，但處理很長序列的時候仍然不可避免。儘管如此，LSTM/GRU 在現有 NLP 任務上已經表現很好了。論文提出門控函式最主要的問題是門的存在使得計算過程無法並行，且增大了計算複雜度。

並且，在多層 LSTM 中，由於還是採用 tanh 函式，在層與層之間的梯度消失仍然沒有解決（這裡主要是的影響），所以現階段的多層 LSTM 多是採用 2~3 層，最多不會超過 4 層。

初始化（IRNN）

Hinton 於 2015 年提出在 RNN 中用 Relu 作為啟用函式。Relu 作為啟用函式用在 RNN 中的弊端在前面已經說明瞭。為瞭解決這個問題，IRNN 將權重矩陣初始化為單位矩陣並將偏置置 0（IRNN的 I 因此得名——Identity Matrix）。

此後，基於 IRNN，有人提出了改進，比如將權重矩陣初始化為正定矩陣，或者增加正則項。但 IRNN 對學習率很敏感，在學習率大時容易梯度爆炸。 

梯度截斷

在反向傳播中，梯度消失/爆炸前會有一個漸變的過程。梯度截斷的意思就是，在漸變過程中，人為設定只傳遞幾步，即人為設定對角矩陣連乘幾次，然後強行拉回正常值水平，再進行梯度下降。該方法對解決梯度問題比較有效，但總有人為的因素，且強行拉回的值不一定準確。有沒有更優雅的方法呢？ 

IndRNN

為瞭解決梯度消失/爆炸問題，IndRNN 引入了 Relu 作為啟用函式，並且將層內的神經元獨立開來。對 RNN 的式子稍加改進，就變成了 IndRNN：

權重繫數從矩陣 U 變成了向量 u 。⊙ 表示矩陣元素積。也即在 t 時刻，每個神經元只接受此刻的輸入以及 t-1 時刻自身的狀態作為輸入。

而傳統 RNN 在 t 時刻每一個神經元都接受 t-1 時刻所有神經元的狀態作為輸入。所以 IndRNN 中的每個神經元可以獨立地處理一份空間 pattern，視覺化也就變得可行了。 現在來看一下梯度問題：

與傳統 RNN 的梯度作對比，可以發現此時的連積操作不再是矩陣操作，而是將啟用函式的導數與迴圈權重繫數獨立起來，使用 Relu 作為啟用函式也就順理成章了。至此，梯度問題完美解決（作者在論文裡有詳細的推導過程）。

神經元之間的相互連線依賴層間互動來完成。也就是說，下一層的神將元會接受上一層所有神經元的輸出作為輸入（相當於全連線層）。

作者在論文裡證明瞭兩層的 IndRNN 相當於一層啟用函式為線性函式、迴圈權重為可對角化矩陣的傳統 RNN。

IndRNN 可實現多層堆疊。因為在多層堆疊結構中，層間互動是全連線方式，因此可以進行改進，比如改全連線方式為 CNN 連線，也可引入 BN、殘差連線等。

實驗介紹

實驗部分首先在三個評估 RNN 模型的常用任務上進行，以驗證 IndRNN 的長程記憶能力和深層網路訓練的可行性，為驗證性實驗。然後在骨骼動作識別任務上進行預測，為實驗性實驗。 

Adding Problem

任務描述：輸入兩個序列，第一個序列是一串在（0，1）之間均勻取樣的數字，第二個序列是一串同等長度的、其中只有兩個數字為 1，其餘為 0 的數字，要求輸出與第二個序列中兩個數字 1 對應的第一個序列中的兩個數字的和。

實驗的序列長度分別為 100，500 和 1000，採用 MSE 作為標的函式。

實驗結果可以看出，IRNN 和 LSTM 都只能處理中等長度的序列（500-1000步），而 IndRNN 可以輕鬆處理時間跨度 5000 步的序列資料。 

Sequential MNIST Classification

任務描述：輸入一串 MINIST 畫素點的資料，然後進行分類。而 pMINIST 則在 MINIST 任務上增加了難度：畫素點資料進行了置換。

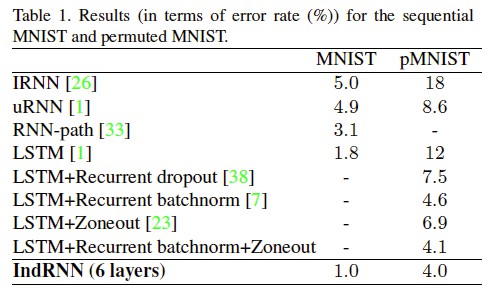
Language Modeling

任務描述：在字元級別 PTB 資料集上進行語言模型的評估。在該任務中，為了驗證 IndRNN 可以構造深層網路，論文裡給出了 21 層 IndRNN 的訓練以及結果。

Skeleton Based Action Recognition

任務描述：使用了 NTU RGB+D 的資料庫，是目前為止最大的基於骨骼的動作識別資料庫。

個人心得

論文裡將層內神經元獨立開來的想法雖然看似簡單，但要想出來還真的不容易。本文為理解 RNN 提供了一個新的角度，也讓 RNN 單個神經元行為的解釋變得可行。此外，Relu 函式的使用也使得 RNN 堆疊結構成為可能。

從實驗結果來看，IndRNN 帶來的效果提升都比較顯著。但有一點是，Relu 函式可能會輸出 0，在序列資料裡意味著之前的歷史資訊全部丟棄。是否換成 Leaky Relu 會更好一點？

本文由 AI 學術社群 PaperWeekly 精選推薦，社群目前已改寫自然語言處理、計算機視覺、人工智慧、機器學習、資料挖掘和資訊檢索等研究方向，點選「閱讀原文」即刻加入社群！

點選標題檢視更多論文解讀： 

• CycleGAN：圖片風格，想換就換

• 基於GAN的字型風格遷移

• 基於置信度的知識圖譜表示學習框架

• 基於檔案級問答任務的新註意力模型

#投 稿 通 道#

投稿須知 | 讓你的文字被很多很多很多人看到

  我是彩蛋