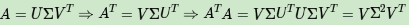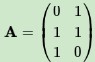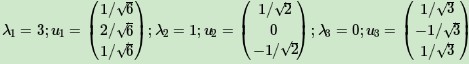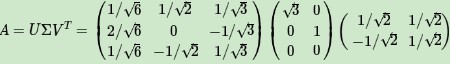【演演算法】SVD演演算法

奇異值分解(Singular Value Decomposition，簡稱SVD)是在機器學習領域廣泛應用的演演算法，它不光可以用於降維演演算法中的特徵分解，還可以用於推薦系統，以及自然語言處理等領域，是很多機器學習演演算法的基石。本文就對SVD的原理做一個總結，並討論在在PCA降維演演算法中是如何運用運用SVD的。

首先回顧下特徵值和特徵向量的定義如下：

Ax=λx

其中A是一個n×n的矩陣，x是一個n維向量，則我們說λ是矩陣A的一個特徵值，而x是矩陣A的特徵值λ所對應的特徵向量。

求出特徵值和特徵向量有什麼好處呢？ 我們可以將矩陣A特徵分解。如果我們求出了矩陣A的n個特徵值λ1≤λ2≤…≤λn,以及這n個特徵值所對應的特徵向量{w1,w2,…wn}，那麼矩陣A就可以用下式的特徵分解表示：

A=WΣW^−1

其中W是這n個特徵向量所張成的n×n維矩陣，而Σ為這n個特徵值為主對角線的n×n維矩陣。一般會把W的這n個特徵向量標準化，即滿足||wi||^2=1, 或者說wi^Twi=1，此時W的n個特徵向量為標準正交基，滿足W^TW=I，即W^T=W^−1, 也就是說W為酉矩陣。這樣特徵分解運算式可以寫成

A=WΣW^T

註意到要進行特徵分解，矩陣A必須為方陣。那麼如果A不是方陣，即行和列不相同時，我們還可以對矩陣進行分解嗎？

SVD也是對矩陣進行分解，但和特徵分解不同，SVD並不要求要分解的矩陣為方陣。假設矩陣A是一個m×n的矩陣，那麼我們定義矩陣A的SVD為：

A=UΣV^T

其中U是一個m×m的矩陣，Σ是一個m×n的矩陣，除了主對角線上的元素以外全為0，主對角線上的每個元素都稱為奇異值，V是一個n×n的矩陣。U和V都是酉矩陣，即滿足U^TU=I,V^TV=I。下圖可以很形象的看出上面SVD的定義：

那麼如何求出SVD分解後的U,Σ,V這三個矩陣呢？如果將A的轉置和A做矩陣乘法，那麼會得到n×n的一個方陣A^TA。既然A^TA是方陣，那麼就可以進行特徵分解，得到的特徵值和特徵向量滿足下式：

這樣就可以得到矩陣A^TA的n個特徵值和對應的n個特徵向量v。將A^TA的所有特徵向量張成一個n×n的矩陣V，就是SVD公式裡面的V矩陣了。一般將V中的每個特徵向量叫做A的右奇異向量。

如果將A和A的轉置做矩陣乘法，那麼會得到m×m的一個方陣AA^T。既然AA^T是方陣，那麼就可以進行特徵分解，得到的特徵值和特徵向量滿足下式：

這樣就可以得到矩陣AA^T的m個特徵值和對應的m個特徵向量u。將AA^T的所有特徵向量張成一個m×m的矩陣U，就是SVD公式裡面的U矩陣。一般將U中的每個特徵向量叫做A的左奇異向量。

U和V求出來後，現在剩下奇異值矩陣Σ沒有求出。由於Σ除了對角線上是奇異值其他位置都是0，那我們只需要求出每個奇異值σ就可以了。註意到:

可以求出我們的每個奇異值，進而求出奇異值矩陣Σ。

上面還有一個問題沒有講，就是說A^TA的特徵向量組成的就是SVD中的V矩陣，而AA^T的特徵向量組成的就是SVD中的U矩陣，這有什麼根據嗎？其實很容易證明，以V矩陣的證明為例。

用一個簡單的例子來說明矩陣是如何進行奇異值分解的。矩陣A定義為：

首先求出A^TA和AA^T

求出A^TA的特徵值和特徵向量：

接著求AA^T的特徵值和特徵向量：

求出奇異值

 最終得到A的奇異值分解為：

上面對SVD的定義和計算做了詳細的描述，似乎看不出SVD有什麼好處。那麼SVD有什麼重要的性質值得我們註意呢？對於奇異值,它跟特徵分解中的特徵值類似，在奇異值矩陣中也是按照從大到小排列，而且奇異值的減少特別的快，在很多情況下，前10%甚至1%的奇異值的和就佔了全部的奇異值之和的99%以上的比例。也就是說，也可以用最大的k個的奇異值和對應的左右奇異向量來近似描述矩陣。也就是說：

如下圖所示，現在矩陣A只需要灰色的部分的三個小矩陣就可以近似描述了。

由於這個重要的性質，SVD可以用於PCA降維，來做資料壓縮和去噪。也可以用於推薦演演算法，將使用者和喜好對應的矩陣做特徵分解，進而得到隱含的使用者需求來做推薦。同時也可以用於NLP中的演演算法，比如潛在語意索引（LSI）。

在主成分分析（PCA）原理總結（機器學習(27)【降維】之主成分分析(PCA)詳解）中講到要用PCA降維，需要找到樣本協方差矩陣X^TX的最大的d個特徵向量，然後用這最大的d個特徵向量張成的矩陣來做低維投影降維。可以看出，在這個過程中需要先求出協方差矩陣X^TX，當樣本數多樣本特徵數也多的時候，這個計算量是很大的。

註意到SVD也可以得到協方差矩陣X^TX最大的d個特徵向量張成的矩陣，但是SVD有個好處，有一些SVD的實現演演算法可以不求先求出協方差矩陣X^TX，也能求出我們的右奇異矩陣V。也就是說，PCA演演算法可以不用做特徵分解，而是做SVD來完成。這個方法在樣本量很大的時候很有效。實際上，scikit-learn的PCA演演算法的背後真正的實現就是用的SVD，而不是我們我們認為的暴力特徵分解。

另一方面，註意到PCA僅僅使用了SVD的右奇異矩陣，沒有使用左奇異矩陣，那麼左奇異矩陣有什麼用呢？

假設樣本是m×n的矩陣X，如果透過SVD找到了矩陣XX^T最大的d個特徵向量張成的m×d維矩陣U，則如果進行如下處理：

可以得到一個d×n的矩陣X‘,這個矩陣和原來的m×n維樣本矩陣X相比，行數從m減到了k，可見對行數進行了壓縮。也就是說，左奇異矩陣可以用於行數的壓縮。相對的，右奇異矩陣可以用於列數即特徵維度的壓縮，也就是PCA降維。　　

SVD作為一個很基本的演演算法，在很多機器學習演演算法中都有它的身影，特別是在現在的大資料時代，由於SVD可以實現並行化，因此更是大展身手。SVD的原理不難，只要有基本的線性代數知識就可以理解，實現也很簡單因此值得仔細的研究。當然，SVD的缺點是分解出的矩陣解釋性往往不強，有點黑盒子的味道，不過這不影響它的使用。