【演演算法】k均值和層次聚類

看看下麵這張圖，有各種各樣的蟲子和蝸牛，你試試將它們分成不同的組別？

完成了嗎？儘管這裡並不一定有所謂的「正確答案」，但一般來說我們可以將這些蟲子分成四組：蜘蛛、蝸牛、蝴蝶/飛蛾、蜜蜂/黃蜂。

很簡單吧？即使蟲子數量再多一倍你也能把它們分清楚，對嗎？你只需要一點時間以及對昆蟲學的熱情就夠了——其實就算有成千上萬隻蟲子你也能將它們分開。

但對於一臺機器而言，將這 10 個物件分類成幾個有意義的分組卻並不簡單——我們知道對於這 10 只蟲子，我們可以有 115,975 種不同的分組方式。如果蟲子數量增加到 20，那它們可能的分組方法將超過 50 萬億種。要是蟲子數量達到 100，那可能的方案數量將超過已知宇宙中的粒子的數量。超過多少呢？據我計算，大約多 500,000,000,000,000,000,000,000,000,000,000,000 倍，已是難以想象的超天文數字！

而我們人類可以做得很快，我們往往會把自己快速分組和理解大量資料的能力看作是理所當然。不管那是一段文字，還是螢幕上影象，或是物件序列，人類通常都能有效地理解自己所面對的資料。

鑒於人工智慧和機器學習的關鍵就是快速理解大量輸入資料，那在開發這些技術方面有什麼捷徑呢？在本文中，你將閱讀到兩種聚類演演算法——k-均值聚類和層次聚類，機器可以用其來快速理解大型資料集。

何時使用？

當你事先知道你將找到多少個分組的時候。

工作方式

該演演算法可以隨機將每個觀測值（observation）分配到 k 類中的一類，然後計算每個類的平均。接下來，它重新將每個觀測值分配到與其最接近的均值的類別，然後再重新計算其均值。這一步不斷重覆，直到不再需要新的分配為止。

有效案例

假設有一組 9 位足球運動員，他們中每個人都在這一賽季進了一定數量的球（假設在 3-30 之間）。然後我們要將他們分成幾組——比如 3 組。

第一步：需要我們將這些運動員隨機分成 3 組並計算每一組的均值。

第二步：對於每一位運動員，將他們重新分配到與他們的分數最接近的均值的那一組；比如，運動員 A（5 個球）被重新分配到第 2 組（均值=11）。然後再計算新的均值。

不斷重覆第二步，直到每一組的均值不再變化。對於這個簡單的任務，下一次迭代就能達到我們的標的。現在就完成了，你已經從原資料集得到了 3 個聚類！

透過這個例子，該聚類可能能夠對應這些運動員在球場上的位置——比如防守、中場和進攻。K-均值在這裡有效，是因為我們可以合理地預測這些資料會自然地落到這三個分組中。

以這種方式，當給定一系串列現統計的資料時，機器就能很好地估計任何足球隊的隊員的位置——可用於體育分析，也能用於任何將資料集分類為預定義分組的其它目的的分類任務。

更加細微的細節：

上面所描述的演演算法還有一些變體。最初的「種子」聚類可以透過多種方式完成。這裡，我們隨機將每位運動員分成了一組，然後計算該組的均值。這會導致最初的均值可能會彼此接近，這會增加後面的步驟。

另一種選擇種子聚類的方法是每組僅一位運動員，然後開始將其他運動員分配到與其最接近的組。這樣傳回的聚類是更敏感的初始種子，從而減少了高度變化的資料集中的重覆性。但是，這種方法有可能減少完成該演演算法所需的迭代次數，因為這些分組實現收斂的時間會變得更少。

K-均值聚類的一個明顯限制是你必須事先提供預期聚類數量的假設。目前也存在一些用於評估特定聚類的擬合的方法。比如說，聚類內平方和（Within-Cluster Sum-of-Squares）可以測量每個聚類內的方差。聚類越好，整體 WCSS 就越低。

何時使用？

當我們希望進一步挖掘觀測資料的潛在關係，可以使用層次聚類演演算法。

工作方式

首先我們會計算距離矩陣（distance matrix），其中矩陣的元素（i，j）代表觀測值 i 和 j 之間的距離度量。然後將最接近的兩個觀察值組為一對，並計算它們的平均值。透過將成對觀察值合併成一個物件，我們生成一個新的距離矩陣。具體合併的過程即計算每一對最近觀察值的均值，並填入新距離矩陣，直到所有觀測值都已合併。

有效案例：

以下是關於鯨魚或海豚物種分類的超簡單資料集。作為受過專業教育的生物學家，我可以保證通常我們會使用更加詳盡的資料集構建系統。現在我們可以看看這六個物種的典型體長。本案例中我們將使用 2 次重覆步驟。

步驟一：計算每個物種之間的距離矩陣，在本案例中使用的是歐氏距離（Euclidean distance），即資料點（data point）間的距離。你可以像在道路地圖上檢視距離圖一樣計算出距離。我們可以透過檢視相關行和列的交叉點值來查閱任一兩物種間的長度差。

步驟二：將兩個距離最近的物種挑選出來，在本案例中是寬吻海豚和灰海豚，他們平均體長達到了 3.3m。重覆第一步，並再一次計算距離矩陣，但這一次將寬吻海豚和灰海豚的資料使用其均值長度 3.3m 代替。

接下來，使用新的距離矩陣重覆步驟二。現在，最近的距離成了領航鯨與逆戟鯨，所以我們計算其平均長度（7.0m），併合併成新的一項。

隨後我們再重覆步驟一，再一次計算距離矩陣，只不過現在將領航鯨與逆戟鯨合併成一項且設定長度為 7.0m。

我們再一次使用現在的距離矩陣重覆步驟 2。最近的距離（3.7m）出現在兩個已經合併的項，現在我們將這兩項合併成為更大的一項（均值為 5.2m）。

緊接著，我們再一次重覆步驟 2，最小距離（5.0m）出現在座頭鯨與長鬚鯨中，所以繼續合併它們為一項，並計算均值（17.5m）。

傳回到步驟 1，計算新的距離矩陣，其中座頭鯨與長鬚鯨已經合併為一項。

最後，重覆步驟 2，距離矩陣中只存在一個值（12.3m），我們將所有的都合成為了一項，並且現在可以停止這一迴圈過程。先讓我們看看最後的合併項。

現在其有一個巢狀結構（參考 JSON），該巢狀結構能繪製成一個樹狀圖。其和家族系譜圖的讀取方式相近。在樹型圖中，兩個觀察值越近，它們就越相似和密切相關。

透過樹型圖的結構，我們能更深入瞭解資料集的結構。在上面的案例中，我們看到了兩個主要的分支，一個分支是 HW 和 FW，另一個是 BD、RD、PW、KW。

在生物進化學中，通常會使用包含更多物種和測量的大型資料集推斷這些物種之間的分類學關係。在生物學之外，層次聚類也在機器學習和資料挖掘中使用。

重要的是，使用這種方法並不需要像 K-均值聚類那樣設定分組的數量。你可以透過給定高度「切割」樹型以傳回分割成的叢集。高度的選擇可以透過幾種方式進行，其取決於我們希望對資料進行聚類的解析度。

例如上圖，如果我們在高度等於 10 的地方畫一條線，就將兩個主分支切開分為兩個子圖。如果我們從高度等於 2 的地方分割，就會生成三個聚類。

更多細節：

對於這裡給出的層次聚類演演算法（hierarchical clustering algorithms），其有三個不同的方面。

最根本的方法就是我們所使用的集聚（agglomerative）過程，透過該過程，我們從單個資料點開始迭代，將資料點聚合到一起，直到成為一個大型的聚類。另外一種（更高計算量）的方法從巨型聚類開始，然後將資料分解為更小的聚類，直到獨立資料點。

還有一些可以計算距離矩陣的方法，對於很多情況下，歐幾裡德距離（參考畢達哥拉斯定理）就已經夠了，但還有一些可選方案在特殊的情境中更加適用。

最後，連線標準（linkage criterion）也可以改變。聚類根據它們不同的距離而連線，但是我們定義「近距離」的方式是很靈活的。在上面的案例中，我們透過測量每一聚類平均值（即形心（centroid））之間的距離，並與最近的聚類進行配對。但你也許會想用其他定義。

例如，每個聚類有幾個離散點組成。我們可以將兩個聚類間的距離定義為任意點間的最小（或最大）距離，就如下圖所示。還有其他方法定義連線標準，它們可能適應於不同的情景。

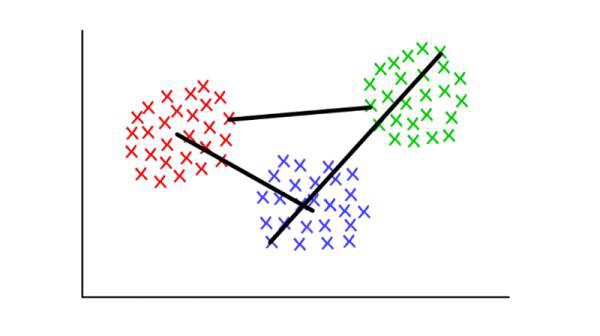
紅/藍：形心連線；紅/綠：最小連線；綠/藍：最大連線