小編邀請您,先思考:
1 GBDT演演算法的原理是什麼?
2 GBDT演演算法如何做正則化處理?
本文對Boosting家族中另一個重要的演演算法梯度提升樹(Gradient Boosting Decison Tree, 以下簡稱GBDT)做一個總結。GBDT有很多簡稱,有GBT(Gradient Boosting Tree), GTB(Gradient Tree Boosting ), GBRT(Gradient Boosting Regression Tree), MART(Multiple Additive Regression Tree),其實都是指的同一種演演算法,本文統一簡稱GBDT。GBDT在BAT大廠中也有廣泛的應用,假如要選擇3個最重要的機器學習演演算法的話,個人認為GBDT應該佔一席之地。
GBDT概述
GBDT也是整合學習Boosting家族的成員,但是卻和傳統的Adaboost有很大的不同。回顧下Adaboost,是利用前一輪迭代弱學習器的誤差率來更新訓練集的權重,這樣一輪輪的迭代下去。GBDT也是迭代,使用了前向分佈演演算法,但是弱學習器限定了只能使用CART回歸樹模型,同時迭代思路和Adaboost也有所不同。
在GBDT的迭代中,假設我們前一輪迭代得到的強學習器是ft−1(x), 損失函式是L(y,ft−1(x)), 我們本輪迭代的標的是找到一個CART回歸樹模型的弱學習器ht(x),讓本輪的損失損失L(y,ft(x)=L(y,ft−1(x)+ht(x))最小。也就是說,本輪迭代找到決策樹,要讓樣本的損失儘量變得更小。
GBDT的思想可以用一個通俗的例子解釋,假如有個人30歲,我們首先用20歲去擬合,發現損失有10歲,這時我們用6歲去擬合剩下的損失,發現差距還有4歲,第三輪我們用3歲擬合剩下的差距,差距就只有一歲了。如果我們的迭代輪數還沒有完,可以繼續迭代下麵,每一輪迭代,擬合的歲數誤差都會減小。
從上面的例子看這個思想還是蠻簡單的,但是有個問題是這個損失的擬合不好度量,損失函式各種各樣,怎麼找到一種通用的擬合方法呢?
負梯度擬合
在上一節中,我們介紹了GBDT的基本思路,但是沒有解決損失函式擬合方法的問題。針對這個問題,大牛Freidman提出了用損失函式的負梯度來擬合本輪損失的近似值,進而擬合一個CART回歸樹。第t輪的第i個樣本的損失函式的負梯度表示為

利用(xi,rti)(i=1,2,..m),我們可以擬合一顆CART回歸樹,得到了第t顆回歸樹,其對應的葉節點區域Rtj,j=1,2,…,J。其中J為葉子節點的個數。
針對每一個葉子節點裡的樣本,我們求出使損失函式最小,也就是擬合葉子節點最好的的輸出值ctj如下:

這樣就得到了本輪的決策樹擬合函式如下:
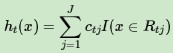
從而本輪最終得到的強學習器的運算式如下:

透過損失函式的負梯度來擬合,找到了一種通用的擬合損失誤差的辦法,這樣無輪是分類問題還是回歸問題,我們透過其損失函式的負梯度的擬合,就可以用GBDT來解決我們的分類回歸問題。區別僅僅在於損失函式不同導致的負梯度不同而已。
回歸演演算法
輸入: 最大迭代次數T, 損失函式L,訓練樣本集

輸出: 強學習器f(x)
1) 初始化弱學習器

2)對迭代輪數t=1,2,…T有:
a) 對樣本i=1,2,…m,計算負梯度

b) 利用(xi,rti)(i=1,2,..m), 擬合一顆CART回歸樹,得到第t顆回歸樹,其對應的葉子節點區域為Rtj,j=1,2,…,J。其中J為回歸樹t的葉子節點的個數。
c) 對葉子區域j =1,2,..J,計算最佳擬合值
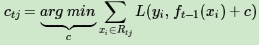
(d) 更新強學習器

3) 得到強學習器f(x)的運算式

分類演演算法
GBDT的分類演演算法從思想上和GBDT的回歸演演算法沒有區別,但是由於樣本輸出不是連續的值,而是離散的類別,導致我們無法直接從輸出類別去擬合類別輸出的誤差。
為瞭解決這個問題,主要有兩個方法,一個是用指數損失函式,此時GBDT退化為Adaboost演演算法。另一種方法是用類似於邏輯回歸的對數似然損失函式的方法。也就是說,我們用的是類別的預測機率值和真實機率值的差來擬合損失。本文僅討論用對數似然損失函式的GBDT分類。而對於對數似然損失函式,我們又有二元分類和多元分類的區別。
二元分類演演算法
對於二元GBDT,如果用類似於邏輯回歸的對數似然損失函式,則損失函式為:
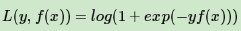
其中y∈{−1,+1}。則此時的負梯度誤差為

對於生成的決策樹,我們各個葉子節點的最佳殘差擬合值為

由於上式比較難最佳化,我們一般使用近似值代替

除了負梯度計算和葉子節點的最佳殘差擬合的線性搜尋,二元GBDT分類和GBDT回歸演演算法過程相同。
多元分類演演算法
多元GBDT要比二元GBDT複雜一些,對應的是多元邏輯回歸和二元邏輯回歸的複雜度差別。假設類別數為K,則此時我們的對數似然損失函式為:

其中如果樣本輸出類別為k,則yk=1。第k類的機率pk(x)的運算式為:

集合上兩式,我們可以計算出第t輪的第i個樣本對應類別l的負梯度誤差為
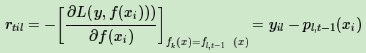
對於生成的決策樹,我們各個葉子節點的最佳殘差擬合值為

由於上式比較難最佳化,我們一般使用近似值代替

除了負梯度計算和葉子節點的最佳殘差擬合的線性搜尋,多元GBDT分類和二元GBDT分類以及GBDT回歸演演算法過程相同。
正則化
和Adaboost一樣,我們也需要對GBDT進行正則化,防止過擬合。GBDT的正則化主要有三種方式。
第一種是和Adaboost類似的正則化項,即步長(learning rate)。定義為ν,對於前面的弱學習器的迭代
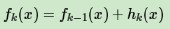
如果我們加上了正則化項,則有

ν的取值範圍為0
第二種正則化的方式是透過子取樣比例(subsample)。取值為(0,1]。註意這裡的子取樣和隨機森林不一樣,隨機森林使用的是放回抽樣,而這裡是不放回抽樣。如果取值為1,則全部樣本都使用,等於沒有使用子取樣。如果取值小於1,則只有一部分樣本會去做GBDT的決策樹擬合。選擇小於1的比例可以減少方差,即防止過擬合,但是會增加樣本擬合的偏差,因此取值不能太低。推薦在[0.5, 0.8]之間。使用了子取樣的GBDT有時也稱作隨機梯度提升樹(Stochastic Gradient Boosting Tree, SGBT)。由於使用了子取樣,程式可以透過取樣分發到不同的任務去做boosting的迭代過程,最後形成新樹,從而減少弱學習器難以並行學習的弱點。
第三種是對於弱學習器即CART回歸樹進行正則化剪枝。在決策樹原理篇裡我們已經講過,這裡就不重覆了
小結
GDBT本身並不複雜,不過要吃透的話需要對整合學習的原理,決策樹原理和各種損失函樹有一定的瞭解。由於GBDT的卓越效能,只要是研究機器學習都應該掌握這個演演算法,包括背後的原理和應用調參方法。目前GBDT的演演算法比較好的庫是xgboost。當然scikit-learn也可以。
優點
1) 可以靈活處理各種型別的資料,包括連續值和離散值。
2) 在相對少的調參時間情況下,預測的準備率也可以比較高。這個是相對SVM來說的。
3)使用一些健壯的損失函式,對異常值的魯棒性非常強。比如 Huber損失函式和Quantile損失函式。
缺點
1) 由於弱學習器之間存在依賴關係,難以並行訓練資料。不過可以透過自取樣的SGBT來達到部分並行。
歡迎分享給他人讓更多的人受益

參考:
-
周志華《機器學習》
-
Neural Networks and Deep Learning by By Michael Nielsen
-
部落格園
http://www.cnblogs.com/pinard/p/6140514.html
-
李航《統計學習方法》
親愛的讀者朋友們,您們有什麼想法,請點選【寫留言】按鈕,寫下您的留言。
資料人網(http://shujuren.org)誠邀各位資料人來平臺分享和傳播優質資料知識。
公眾號推薦:
好又樂書屋,專註分享有思想的人物,身心健康,自我教育,閱讀寫作和有趣味的生活等內容,傳播正能量。

閱讀原文,更多精彩!
分享是收穫,傳播是價值!
 知識星球
知識星球