小編邀請您,先思考:
1 Adaboost演演算法的原理是什麼 ?
2 Adaboost演演算法如何實現?
1 Adaboost的原理
1.1 Adaboost是什麼
AdaBoost,是英文”Adaptive Boosting”(自適應增強)的縮寫,由Yoav Freund和Robert Schapire在1995年提出。它的自適應在於:前一個基本分類器分錯的樣本會得到加強,加權後的全體樣本再次被用來訓練下一個基本分類器。同時,在每一輪中加入一個新的弱分類器,直到達到某個預定的足夠小的錯誤率或達到預先指定的最大迭代次數。

具體說來,整個Adaboost 迭代演演算法就3步:
-
初始化訓練資料的權值分佈。如果有N個樣本,則每一個訓練樣本最開始時都被賦予相同的權值:1/N。
-
訓練弱分類器。具體訓練過程中,如果某個樣本點已經被準確地分類,那麼在構造下一個訓練集中,它的權值就被降低;相反,如果某個樣本點沒有被準確地分類,那麼它的權值就得到提高。然後,權值更新過的樣本集被用於訓練下一個分類器,整個訓練過程如此迭代地進行下去。
-
將各個訓練得到的弱分類器組合成強分類器。各個弱分類器的訓練過程結束後,加大分類誤差率小的弱分類器的權重,使其在最終的分類函式中起著較大的決定作用,而降低分類誤差率大的弱分類器的權重,使其在最終的分類函式中起著較小的決定作用。換言之,誤差率低的弱分類器在最終分類器中佔的權重較大,否則較小。
1.2 Adaboost演演算法流程
給定一個訓練資料集T={(x1,y1), (x2,y2)…(xN,yN)},其中實體x \in \mathcal{X},而實體空間\mathcal{X} \subset \mathbb{R}^n,yi屬於標記集合{-1,+1},Adaboost的目的就是從訓練資料中學習一系列弱分類器或基本分類器,然後將這些弱分類器組合成一個強分類器。
Adaboost的演演算法流程如下:
-
步驟1. 首先,初始化訓練資料的權值分佈。每一個訓練樣本最開始時都被賦予相同的權值:1/N。
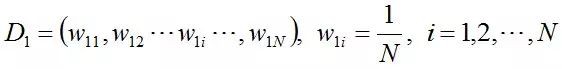
-
步驟2. 進行多輪迭代,用m = 1,2, …, M表示迭代的第多少輪
-
使用具有權值分佈Dm的訓練資料集學習,得到基本分類器(選取讓誤差率最低的閾值來設計基本分類器):

-
計算Gm(x)在訓練資料集上的分類誤差率

由上述式子可知,Gm(x)在訓練資料集上的誤差率em就是被Gm(x)誤分類樣本的權值之和。
-
計算Gm(x)的繫數,am表示Gm(x)在最終分類器中的重要程度(目的:得到基本分類器在最終分類器中所佔的權重):

由上述式子可知,em <= 1/2時,am >= 0,且am隨著em的減小而增大,意味著分類誤差率越小的基本分類器在最終分類器中的作用越大。
-
更新訓練資料集的權值分佈(目的:得到樣本的新的權值分佈),用於下一輪迭代

使得被基本分類器Gm(x)誤分類樣本的權值增大,而被正確分類樣本的權值減小。就這樣,透過這樣的方式,AdaBoost方法能“重點關註”或“聚焦於”那些較難分的樣本上。
其中,Zm是規範化因子,使得Dm+1成為一個機率分佈:

-
步驟3. 組合各個弱分類器

從而得到最終分類器,如下:

1.3 Adaboost的一個例子
下麵,給定下列訓練樣本,請用AdaBoost演演算法學習一個強分類器。

求解過程:初始化訓練資料的權值分佈,令每個權值W1i = 1/N = 0.1,其中,N = 10,i = 1,2, …, 10,然後分別對於m = 1,2,3, …等值進行迭代。
拿到這10個資料的訓練樣本後,根據 X 和 Y 的對應關係,要把這10個資料分為兩類,一類是“1”,一類是“-1”,根據資料的特點發現:“0 1 2”這3個資料對應的類是“1”,“3 4 5”這3個資料對應的類是“-1”,“6 7 8”這3個資料對應的類是“1”,9是比較孤獨的,對應類“-1”。拋開孤獨的9不講,“0 1 2”、“3 4 5”、“6 7 8”這是3類不同的資料,分別對應的類是1、-1、1,直觀上推測可知,可以找到對應的資料分界點,比如2.5、5.5、8.5 將那幾類資料分成兩類。當然,這隻是主觀臆測,下麵實際計算下這個具體過程。
迭代過程1
對於m=1,在權值分佈為D1(10個資料,每個資料的權值皆初始化為0.1)的訓練資料上,經過計算可得:
-
閾值v取2.5時誤差率為0.3(x < 2.5時取1,x > 2.5時取-1,則6 7 8分錯,誤差率為0.3),
-
閾值v取5.5時誤差率最低為0.4(x < 5.5時取1,x > 5.5時取-1,則3 4 5 6 7 8皆分錯,誤差率0.6大於0.5,不可取。故令x > 5.5時取1,x < 5.5時取-1,則0 1 2 9分錯,誤差率為0.4),
-
閾值v取8.5時誤差率為0.3(x < 8.5時取1,x > 8.5時取-1,則3 4 5分錯,誤差率為0.3)。
可以看到,無論閾值v取2.5,還是8.5,總得分錯3個樣本,故可任取其中任意一個如2.5,弄成第一個基本分類器為:

上面說閾值v取2.5時則6 7 8分錯,所以誤差率為0.3,更加詳細的解釋是:因為樣本集中
-
0 1 2對應的類(Y)是1,因它們本身都小於2.5,所以被G1(x)分在了相應的類“1”中,分對了。
-
3 4 5本身對應的類(Y)是-1,因它們本身都大於2.5,所以被G1(x)分在了相應的類“-1”中,分對了。
-
但6 7 8本身對應類(Y)是1,卻因它們本身大於2.5而被G1(x)分在了類”-1″中,所以這3個樣本被分錯了。
-
9本身對應的類(Y)是-1,因它本身大於2.5,所以被G1(x)分在了相應的類“-1”中,分對了。
從而得到G1(x)在訓練資料集上的誤差率(被G1(x)誤分類樣本“6 7 8”的權值之和)e1=P(G1(xi)≠yi) = 3*0.1 = 0.3。
然後根據誤差率e1計算G1的繫數:

這個a1代表G1(x)在最終的分類函式中所佔的權重,為0.4236。
接著更新訓練資料的權值分佈,用於下一輪迭代:
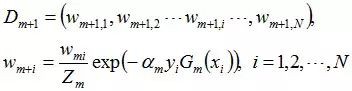
值得一提的是,由權值更新的公式可知,每個樣本的新權值是變大還是變小,取決於它是被分錯還是被分正確。
即如果某個樣本被分錯了,則yi * Gm(xi)為負,負負得正,結果使得整個式子變大(樣本權值變大),否則變小。
第一輪迭代後,最後得到各個資料新的權值分佈D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)。由此可以看出,因為樣本中是資料“6 7 8”被G1(x)分錯了,所以它們的權值由之前的0.1增大到0.1666,反之,其它資料皆被分正確,所以它們的權值皆由之前的0.1減小到0.0715。
分類函式f1(x)= a1*G1(x) = 0.4236G1(x)。
此時,得到的第一個基本分類器sign(f1(x))在訓練資料集上有3個誤分類點(即6 7 8)。
從上述第一輪的整個迭代過程可以看出:被誤分類樣本的權值之和影響誤差率,誤差率影響基本分類器在最終分類器中所佔的權重。
迭代過程2
對於m=2,在權值分佈為D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)的訓練資料上,經過計算可得:
-
閾值v取2.5時誤差率為0.1666*3(x < 2.5時取1,x > 2.5時取-1,則6 7 8分錯,誤差率為0.1666*3),
-
閾值v取5.5時誤差率最低為0.0715*4(x > 5.5時取1,x < 5.5時取-1,則0 1 2 9分錯,誤差率為0.0715*3 + 0.0715),
-
閾值v取8.5時誤差率為0.0715*3(x < 8.5時取1,x > 8.5時取-1,則3 4 5分錯,誤差率為0.0715*3)。
所以,閾值v取8.5時誤差率最低,故第二個基本分類器為:

面對的還是下述樣本:

很明顯,G2(x)把樣本“3 4 5”分錯了,根據D2可知它們的權值為0.0715, 0.0715, 0.0715,所以G2(x)在訓練資料集上的誤差率e2=P(G2(xi)≠yi) = 0.0715 * 3 = 0.2143。
計算G2的繫數:

更新訓練資料的權值分佈:

D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455)。被分錯的樣本“3 4 5”的權值變大,其它被分對的樣本的權值變小。
f2(x)=0.4236G1(x) + 0.6496G2(x)
此時,得到的第二個基本分類器sign(f2(x))在訓練資料集上有3個誤分類點(即3 4 5)。
迭代過程3
對於m=3,在權值分佈為D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455)的訓練資料上,經過計算可得:
-
閾值v取2.5時誤差率為0.1060*3(x < 2.5時取1,x > 2.5時取-1,則6 7 8分錯,誤差率為0.1060*3),
-
閾值v取5.5時誤差率最低為0.0455*4(x > 5.5時取1,x < 5.5時取-1,則0 1 2 9分錯,誤差率為0.0455*3 + 0.0715),
-
閾值v取8.5時誤差率為0.1667*3(x < 8.5時取1,x > 8.5時取-1,則3 4 5分錯,誤差率為0.1667*3)。
所以閾值v取5.5時誤差率最低,故第三個基本分類器為:

依然還是原樣本:

此時,被誤分類的樣本是:0 1 2 9,這4個樣本所對應的權值皆為0.0455,
所以G3(x)在訓練資料集上的誤差率e3 = P(G3(xi)≠yi) = 0.0455*4 = 0.1820。
計算G3的繫數:
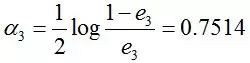
更新訓練資料的權值分佈:

D4 = (0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125)。被分錯的樣本“0 1 2 9”的權值變大,其它被分對的樣本的權值變小。
f3(x)=0.4236G1(x) + 0.6496G2(x)+0.7514G3(x)
此時,得到的第三個基本分類器sign(f3(x))在訓練資料集上有0個誤分類點。至此,整個訓練過程結束。
現在,咱們來總結下3輪迭代下來,各個樣本權值和誤差率的變化,如下所示(其中,樣本權值D中加了下劃線的表示在上一輪中被分錯的樣本的新權值):
-
訓練之前,各個樣本的權值被初始化為D1 = (0.1, 0.1,0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1);
-
第一輪迭代中,樣本“6 7 8”被分錯,對應的誤差率為e1=P(G1(xi)≠yi) = 3*0.1 = 0.3,此第一個基本分類器在最終的分類器中所佔的權重為a1 = 0.4236。第一輪迭代過後,樣本新的權值為D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715);
-
第二輪迭代中,樣本“3 4 5”被分錯,對應的誤差率為e2=P(G2(xi)≠yi) = 0.0715 * 3 = 0.2143,此第二個基本分類器在最終的分類器中所佔的權重為a2 = 0.6496。第二輪迭代過後,樣本新的權值為D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455);
-
第三輪迭代中,樣本“0 1 2 9”被分錯,對應的誤差率為e3 = P(G3(xi)≠yi) = 0.0455*4 = 0.1820,此第三個基本分類器在最終的分類器中所佔的權重為a3 = 0.7514。第三輪迭代過後,樣本新的權值為D4 = (0.125, 0.125, 0.125, 0.102, 0.102, 0.102, 0.065, 0.065, 0.065, 0.125)。
從上述過程中可以發現,如果某些個樣本被分錯,它們在下一輪迭代中的權值將被增大,同時,其它被分對的樣本在下一輪迭代中的權值將被減小。就這樣,分錯樣本權值增大,分對樣本權值變小,而在下一輪迭代中,總是選取讓誤差率最低的閾值來設計基本分類器,所以誤差率e(所有被Gm(x)誤分類樣本的權值之和)不斷降低。
綜上,將上面計算得到的a1、a2、a3各值代入G(x)中,G(x) = sign[f3(x)] = sign[ a1 * G1(x) + a2 * G2(x) + a3 * G3(x) ],得到最終的分類器為:
G(x) = sign[f3(x)] = sign[ 0.4236G1(x) + 0.6496G2(x)+0.7514G3(x) ]。
2 Adaboost的誤差界
透過上面的例子可知,Adaboost在學習的過程中不斷減少訓練誤差e,直到各個弱分類器組合成最終分類器,那這個最終分類器的誤差界到底是多少呢?
事實上,Adaboost 最終分類器的訓練誤差的上界為:

下麵,咱們來透過推導來證明下上述式子。
當G(xi)≠yi時,yi*f(xi)<0,因而exp(-yi*f(xi))≥1,因此前半部分得證。
關於後半部分,別忘了:

整個的推導過程如下:

這個結果說明,可以在每一輪選取適當的Gm使得Zm最小,從而使訓練誤差下降最快。接著,咱們來繼續求上述結果的上界。
對於二分類而言,有如下結果:

其中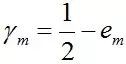
繼續證明下這個結論。
由之前Zm的定義式跟本節最開始得到的結論可知:
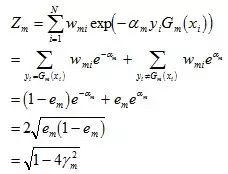
而這個不等式 可先由e^x和1-x的開根號,在點x的泰勒展開式推出。
可先由e^x和1-x的開根號,在點x的泰勒展開式推出。
值得一提的是,如果取γ1, γ2… 的最小值,記做γ(顯然,γ≥γi>0,i=1,2,…m),則對於所有m,有:

這個結論表明,AdaBoost的訓練誤差是以指數速率下降的。另外,AdaBoost演演算法不需要事先知道下界γ,AdaBoost具有自適應性,它能適應弱分類器各自的訓練誤差率 。
最後,Adaboost 還有另外一種理解,即可以認為其模型是加法模型、損失函式為指數函式、學習演演算法為前向分步演演算法的二類分類學習方法,下個月即12月份會再推導下,然後更新此文。而在此之前,有興趣的可以參看《統計學習方法》第8.3節或其它相關資料。
3 Adaboost 指數損失函式推導
事實上,在上文1.2節Adaboost的演演算法流程的步驟3中,我們構造的各個基本分類器的線性組合

是一個加法模型,而Adaboost演演算法其實是前向分步演演算法的特例。那麼問題來了,什麼是加法模型,什麼又是前向分步演演算法呢?
3.1 加法模型和前向分步演演算法
如下圖所示的便是一個加法模型
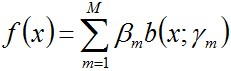
其中, 稱為基函式,
稱為基函式,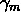 稱為基函式的引數,
稱為基函式的引數,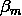 稱為基函式的繫數。
稱為基函式的繫數。
在給定訓練資料及損失函式 的條件下,學習加法模型
的條件下,學習加法模型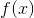 成為經驗風險極小化問題,即損失函式極小化問題:
成為經驗風險極小化問題,即損失函式極小化問題:

隨後,該問題可以作如此簡化:從前向後,每一步只學習一個基函式及其繫數,逐步逼近上式,即:每步只最佳化如下損失函式:
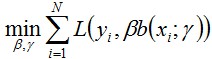
這個最佳化方法便就是所謂的前向分步演演算法。
下麵,咱們來具體看下前向分步演演算法的演演算法流程:
-
輸入:訓練資料集
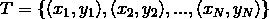
-
損失函式:

-
基函式集:
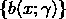
-
輸出:加法模型
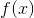
-
演演算法步驟:
初始化
對於m=1,2,..M
a) 極小化損失函式
得到引數
和
b) 更新
最終得到加法模型
就這樣,前向分步演演算法將同時求解從m=1到M的所有引數(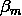 、
、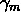 )的最佳化問題簡化為逐次求解各個
)的最佳化問題簡化為逐次求解各個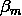 、
、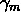 (1≤m≤M)的最佳化問題。
(1≤m≤M)的最佳化問題。
3.2 前向分步演演算法與Adaboost的關係
在上文第2節最後,我們說Adaboost 還有另外一種理解,即可以認為其模型是加法模型、損失函式為指數函式、學習演演算法為前向分步演演算法的二類分類學習方法。其實,Adaboost演演算法就是前向分步演演算法的一個特例,Adaboost 中,各個基本分類器就相當於加法模型中的基函式,且其損失函式為指數函式。
換句話說,當前向分步演演算法中的基函式為Adaboost中的基本分類器時,加法模型等價於Adaboost的最終分類器

你甚至可以說,這個最終分類器其實就是一個加法模型。只是這個加法模型由基本分類器及其系陣列成,m = 1, 2, …, M。前向分步演演算法逐一學習基函式的過程,與Adaboost演演算法逐一學習各個基本分類器的過程一致。
下麵,咱們便來證明:當前向分步演演算法的損失函式是指數損失函式

時,其學習的具體操作等價於Adaboost演演算法的學習過程。
假設經過m-1輪迭代,前向分步演演算法已經得到 :
:

而後在第m輪迭代得到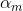 、
、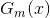 和
和 。其中,
。其中, 為:
為:

而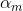 和
和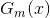 未知。所以,現在咱們的標的便是根據前向分步演演算法訓練
未知。所以,現在咱們的標的便是根據前向分步演演算法訓練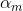 和
和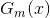 ,使得最終
,使得最終 在訓練資料集T上的指數損失最小,即
在訓練資料集T上的指數損失最小,即

針對這種需要求解多個引數的情況,可以先固定其它引數,求解其中一兩個引數,然後逐一求解剩下的引數。例如我們可以固定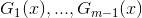 和
和 ,只針對
,只針對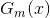 和
和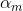 做最佳化。
做最佳化。
換言之,在面對 和
和 這2m個引數都未知的情況下,可以:
這2m個引數都未知的情況下,可以:
-
先假定
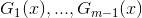 和
和 已知,求解出
已知,求解出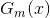 和
和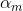 ;
; -
然後再逐一求解其它未知引數。
且考慮到上式中的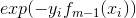 既不依賴
既不依賴 也不依賴G,所以是個與最小化無關的固定值,記為
也不依賴G,所以是個與最小化無關的固定值,記為 ,即
,即

則上式可以表示為(後面要多次用到這個式子,簡記為 ):
):

值得一提的是, 雖然與最小化無關,但
雖然與最小化無關,但 依賴於
依賴於 ,隨著每一輪迭代而發生變化。
,隨著每一輪迭代而發生變化。
接下來,便是要證使得上式達到最小的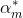 和
和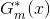 就是Adaboost演演算法所求解得到的
就是Adaboost演演算法所求解得到的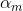 和
和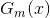 。
。
為求解上式,咱們先求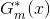 再求
再求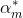 。
。
首先求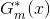 。對於任意
。對於任意 ,使上式
,使上式 最小的G(x)由下式得到:
最小的G(x)由下式得到:

別忘了,

跟1.2節所述的誤差率的計算公式對比下:

可知,上面得到的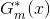 便是Adaboost演演算法的基本分類器
便是Adaboost演演算法的基本分類器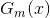 ,因為它是在第m輪加權訓練資料時,使分類誤差率最小的基本分類器。換言之,這個
,因為它是在第m輪加權訓練資料時,使分類誤差率最小的基本分類器。換言之,這個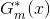 便是Adaboost演演算法所要求的
便是Adaboost演演算法所要求的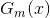 ,別忘了,在Adaboost演演算法的每一輪迭代中,都是選取讓誤差率最低的閾值來設計基本分類器。
,別忘了,在Adaboost演演算法的每一輪迭代中,都是選取讓誤差率最低的閾值來設計基本分類器。
然後求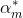 。還是回到之前的這個式子
。還是回到之前的這個式子 上:
上:

這個式子的後半部分可以進一步化簡,得:
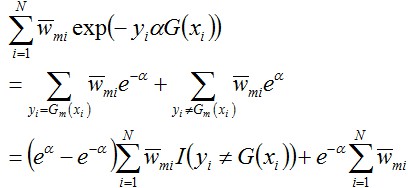
接著將上面求得的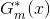

代入上式中,且對 求導,令其求導結果為0,即得到使得
求導,令其求導結果為0,即得到使得 一式最小的
一式最小的 ,即為:
,即為:
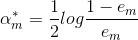
這裡的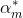 跟上文1.2節中
跟上文1.2節中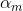 的計算公式完全一致。
的計算公式完全一致。
此外,毫無疑問,上式中的 便是誤差率:
便是誤差率:
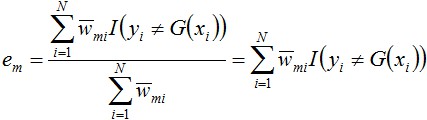
即 就是被Gm(x)誤分類樣本的權值之和。
就是被Gm(x)誤分類樣本的權值之和。
就這樣,結合模型


可以推出

從而有:
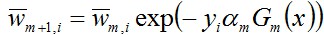
與上文1.2節介紹的權值更新公式
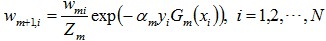
相比,只相差一個規範化因子,即後者多了一個

所以,整個過程下來,我們可以看到,前向分步演演算法逐一學習基函式的過程,確實是與Adaboost演演算法逐一學習各個基本分類器的過程一致,兩者完全等價。
綜上,本節不但提供了Adaboost的另一種理解:加法模型,損失函式為指數函式,學習演演算法為前向分步演演算法,而且也解釋了最開始1.2節中基本分類器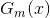 及其繫數
及其繫數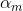 的由來,以及對權值更新公式的解釋,你甚至可以認為本節就是對上文整個1.2節的解釋。
的由來,以及對權值更新公式的解釋,你甚至可以認為本節就是對上文整個1.2節的解釋。
4 參考文獻與推薦閱讀
-
wikipedia上關於Adaboost的介紹:http://zh.wikipedia.org/zh-cn/AdaBoost;
-
鄒博之決策樹與Adaboost PPT:http://pan.baidu.com/s/1hqePkdY;
-
鄒博講Adaboost指數損失函式推導的PPT:http://pan.baidu.com/s/1kTkkepD(第85頁~第98頁);
-
《統計學習方法 李航著》第8章;
-
關於adaboost的一些淺見:http://blog.sina.com.cn/s/blog_6ae183910101chcg.html;
-
A Short Introduction to Boosting:http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.93.5148&rep;=rep1&type;=pdf;
-
南大周志華教授做的關於boosting 25年的報告PPT:http://vdisk.weibo.com/s/FcILTUAi9m111;
-
《資料挖掘十大演演算法》第7章 Adaboost;
-
http://summerbell.iteye.com/blog/532376;
-
統計學習那些事:http://cos.name/2011/12/stories-about-statistical-learning/;
-
統計學習基礎學習筆記:http://www.loyhome.com/%E2%89%AA%E7%BB%9F%E8%AE%A1%E5%AD%A6%E4%B9%A0%E7%B2%BE%E8%A6%81the-elements-of-statistical-learning%E2%89%AB%E8%AF%BE%E5%A0%82%E7%AC%94%E8%AE%B0%EF%BC%88%E5%8D%81%E5%9B%9B%EF%BC%89/;
-
PRML第十四章組合模型讀書筆記:http://vdisk.weibo.com/s/DmxNcM5_IaUD;
-
順便推薦一個非常實用的線上編輯LaTeX 公式的網頁:http://www.codecogs.com/latex/eqneditor.php?lang=zh-cn。
連結:blog.csdn.net/v_july_v/article/details/40718799
親愛的讀者朋友們,您們有什麼想法,請點選【寫留言】按鈕,寫下您的留言。
資料人網(http://shujuren.org)誠邀各位資料人來平臺分享和傳播優質資料知識。
公眾號推薦:
好又樂書屋,專註分享有思想的人物,身心健康,自我教育,閱讀寫作和有趣味的生活等內容,傳播正能量。

閱讀原文,更多精彩!
分享是收穫,傳播是價值!
 知識星球
知識星球