小編邀請您,先思考:
1 樸素貝葉斯公式是什麼?
2 樸素貝葉斯的假設是什麼?
3 樸素貝葉斯是如何分類?
本文介紹一下樸素貝葉斯分類演演算法,講一下基本原理,再以文字分類實踐。
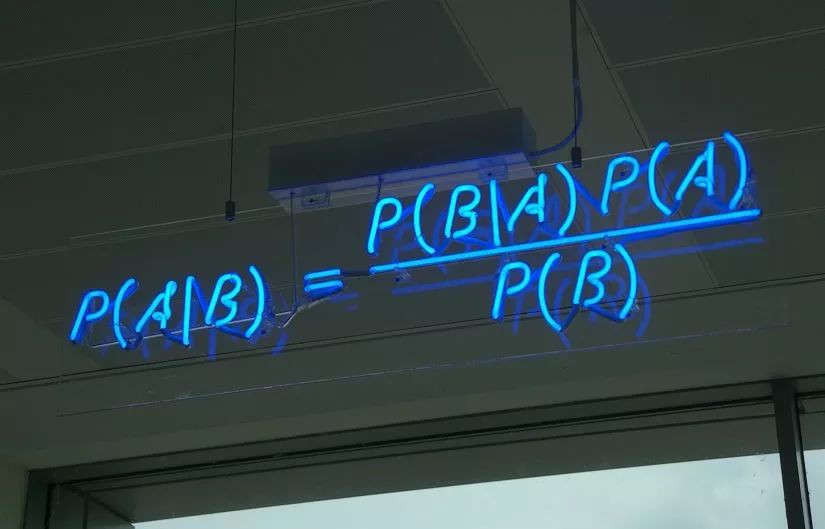
一個簡單的例子
樸素貝葉斯演演算法是一個典型的統計學習方法,主要理論基礎就是一個貝葉斯公式,貝葉斯公式的基本定義如下:

這個公式雖然看上去簡單,但它卻能總結歷史,預知未來。公式的右邊是總結歷史,公式的左邊是預知未來,如果把Y看出類別,X看出特徵,P(Yk|X)就是在已知特徵X的情況下求Yk類別的機率,而對P(Yk|X)的計算又全部轉化到類別Yk的特徵分佈上來。
舉個例子,大學的時候,某男生經常去圖書室晚自習,發現他喜歡的那個女生也常去那個自習室,心中竊喜,於是每天買點好吃點在那個自習室蹲點等她來,可是人家女生不一定每天都來,眼看天氣漸漸炎熱,圖書館又不開空調,如果那個女生沒有去自修室,該男生也就不去,每次男生鼓足勇氣說:“嘿,你明天還來不?”,“啊,不知道,看情況”。
然後該男生每天就把她去自習室與否以及一些其他情況做一下記錄,用Y表示該女生是否去自習室,即Y={去,不去},X是跟去自修室有關聯的一系列條件,比如當天上了哪門主課,蹲點統計了一段時間後,該男生打算今天不再蹲點,而是先預測一下她會不會去,現在已經知道了今天上了常微分方法這麼主課,於是計算P(Y=去|常微分方程)與P(Y=不去|常微分方程),看哪個機率大,
如果 P(Y=去|常微分方程) > P(Y=不去|常微分方程),那這個男生不管多熱都屁顛屁顛去自習室了,否則不就去自習室受罪了。P(Y=去|常微分方程)的計算可以轉為計算以前她去的情況下,那天主課是常微分的機率P(常微分方程|Y=去),註意公式右邊的分母對每個類別(去/不去)都是一樣的,所以計算的時候忽略掉分母,這樣雖然得到的機率值已經不再是0~1之間,但是其大小還是能選擇類別。
後來他發現還有一些其他條件可以挖,比如當天星期幾、當天的天氣,以及上一次與她在自修室的氣氛,統計了一段時間後,該男子一計算,發現不好算了,因為總結歷史的公式:

這裡n=3,x(1)表示主課,x(2)表示天氣,x(3)表示星期幾,x(4)表示氣氛,Y仍然是{去,不去},現在主課有8門,天氣有晴、雨、陰三種、氣氛有A+,A,B+,B,C五種,那麼總共需要估計的引數有8*3*7*5*2=1680個,每天只能收集到一條資料,那麼等湊齊1680條資料大學都畢業了,男生打呼不妙,於是做了一個獨立性假設,假設這些影響她去自習室的原因是獨立互不相關的,於是

有了這個獨立假設後,需要估計的引數就變為,(8+3+7+5)*2 = 46個了,而且每天收集的一條資料,可以提供4個引數,這樣該男生就預測越來越準了。
樸素貝葉斯分類器
講了上面的小故事,我們來樸素貝葉斯分類器的表示形式:

當特徵為為x時,計算所有類別的條件機率,選取條件機率最大的類別作為待分類的類別。由於上公式的分母對每個類別都是一樣的,因此計算時可以不考慮分母,即

樸素貝葉斯的樸素體現在其對各個條件的獨立性假設上,加上獨立假設後,大大減少了引數假設空間。
在文字分類上的應用
文字分類的應用很多,比如垃圾郵件和垃圾簡訊的過濾就是一個2分類問題,新聞分類、文字情感分析等都可以看成是文字分類問題,分類問題由兩步組成:訓練和預測,要建立一個分類模型,至少需要有一個訓練資料集。貝葉斯模型可以很自然地應用到文字分類上:現在有一篇檔案d(Document),判斷它屬於哪個類別ck,只需要計算檔案d屬於哪一個類別的機率最大:

在分類問題中,我們並不是把所有的特徵都用上,對一篇檔案d,我們只用其中的部分特徵詞項

註意P(Ck|d)只是正比於後面那部分公式,完整的計算還有一個分母,但我們前面討論了,對每個類別而已分母都是一樣的,於是在我們只需要計算分子就能夠進行分類了。實際的計算過程中,多個機率值P(tj|ck)的連乘很容易下上限溢位為0,因此轉化為對數計算,連乘就變成了累加:

我們只需要從訓練資料集中,計算每一個類別的出現機率P(ck)和每一個類別中各個特徵詞項的機率P(tj|ck),而這些機率值的計算都採用最大似然估計,說到底就是統計每個詞在各個類別中出現的次數和各個類別的檔案的數目:
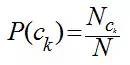

其中,Nck表示訓練集中ck類檔案的數目,N訓練集中檔案總數;Tjk表示詞項tj在類別ck中出現的次數,V是所有類別的詞項集合。這裡對詞的位置作了獨立性假設,即兩個詞只要它們出現的次數一樣,那不管它們在檔案的出現位置,它們大機率值P(tj|ck)都是一樣,這個位置獨立性假設與現實很不相符,比如“放馬屁”跟“馬放屁”表述的是不同的內容,但實踐發現,位置獨立性假設得到的模型準確率並不低,因為大多數文字分類都是靠詞的差異來區分,而不是詞的位置,如果考慮詞的位置,那麼問題將表達相當複雜,以至於我們無從下手。
然後需要註意的一個問題是ti可能沒有出現在ck類別的訓練集,卻出現在ck類別的測試集合中,這樣因為Tik為0,導致連乘機率值都為0,其他特徵詞出現得再多,該檔案也不會被分到ck類別,而且在對數累加的情況下,0值導致計算錯誤,處理這種問題的方法是取樣加1平滑,即認為每個詞在各個類別中都至少出現過一次,即

下麵這個例子來自於參考文獻1,假設有如下的訓練集合測試集:

現在要計算docID為5的測試檔案是否屬於China類別,首先計算個各類的機率,P(c=China)=3/4,P(c!=China)=1/4,然後計算各個類中詞項的機率:
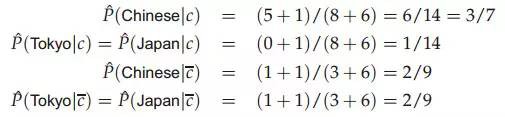
註意分母(8+6)中8表示China類的詞項出現的總次數是8,+6表示平滑,6是總詞項的個數,然後計算測試檔案屬於各個類別的機率:

可以看出該測試檔案應該屬於CHina類別。
文字分類實踐
我找了搜狗的搜狐新聞資料的歷史簡潔版,總共包括汽車、財經、it、健康等9類新聞,一共16289條新聞,搜狗給的資料是每一篇新聞用一個txt檔案儲存,我預處理了一下,把所有的新聞檔案儲存在一個文字檔案中,每一行是一篇新聞,同時保留新聞的id,id的首字母表示類標,預處理並分詞後的示例如下:

我用6289條新聞作為訓練集,剩餘1萬條用於測試,採用互資訊進行文字特徵的提取,總共提取的特徵詞是700個左右。
分類的結果如下:
8343100000.8343
總共10000條新聞,分類正確的8343條,正確率0.8343,這裡主要是演示貝葉斯的分類過程,只考慮了正確率也沒有考慮其他評價指標,也沒有進行最佳化。貝葉斯分類的效率高,訓練時,只需要掃描一遍訓練集,記錄每個詞出現的次數,以及各類檔案出現的次數,測試時也只需要掃描一次測試集,從執行效率這個角度而言,樸素貝葉斯的效率是最高的,而準確率也能達到一個理想的效果。
我的實現程式碼如下:
#!encoding=utf-8
import random
import sys
import math
import collections
import sys
def shuffle():
”’將原來的文字打亂順序,用於得到訓練集和測試集”’
datas = [line.strip() for line in sys.stdin]
random.shuffle(datas)
for line in datas:
print line
lables = [‘A’,’B’,’C’,’D’,’E’,’F’,’G’,’H’,’I’]
def lable2id(lable):
for i in xrange(len(lables)):
if lable == lables[i]:
return i
raise Exception(‘Error lable %s’ % (lable))
def docdict():
return [0]*len(lables)
def mutalInfo(N,Nij,Ni_,N_j):
#print N,Nij,Ni_,N_j
return Nij * 1.0 / N * math.log(N * (Nij+1)*1.0/(Ni_*N_j))/ math.log(2)
def countForMI():
”’基於統計每個詞在每個類別出現的次數,以及每類的檔案數”’
docCount = [0] * len(lables)
#每個類的詞數目
wordCount = collections.defaultdict(docdict)
for line in sys.stdin:
lable,text = line.strip().split(‘ ‘,1)
index = lable2id(lable[0])
words = text.split(‘ ‘)
for word in words:
wordCount[word][index] += 1
docCount[index] += 1
miDict = collections.defaultdict(docdict)
#互資訊值
N = sum(docCount)
for k,vs in wordCount.items():
for i in xrange(len(vs)):
N11 = vs[i]
N10 = sum(vs) – N11
N01 = docCount[i] – N11
N00 = N – N11 – N10 – N01
mi = mutalInfo(N,N11,N10+N11,N01+N11) + mutalInfo(N,N10,N10+N11,N00+N10)+ mutalInfo(N,N01,N01+N11,N01+N00)+ mutalInfo(N,N00,N00+N10,N00+N01)
miDict[k][i] = mi
fWords = set()
for i in xrange(len(docCount)):
keyf = lambda x:x[1][i]
sortedDict = sorted(miDict.items(),key=keyf,reverse=True)
for j in xrange(100):
fWords.add(sortedDict[j][0])
print docCount
#列印各個類的檔案數目
for fword in fWords:
print fword
def loadFeatureWord():
”’匯入特徵詞”’
f = open(‘feature.txt’)
docCounts = eval(f.readline())
features = set()
for line in f:
features.add(line.strip())
f.close()
return docCounts,features
def trainBayes():
”’訓練貝葉斯模型,實際上計算每個類中特徵詞的出現次數”’
docCounts,features = loadFeatureWord()
wordCount = collections.defaultdict(docdict)
tCount = [0]*len(docCounts)
#每類檔案特徵詞出現的次數
for line in sys.stdin:
lable,text = line.strip().split(‘ ‘,1)
index = lable2id(lable[0])
words = text.split(‘ ‘)
for word in words:
if word in features:
tCount[index] += 1
wordCount[word][index] += 1
for k,v in wordCount.items():
scores = [(v[i]+1) * 1.0 / (tCount[i]+len(wordCount)) for i in xrange(len(v))]
#加1平滑
print ‘%s\t%s’ % (k,scores)
def loadModel():
”’匯入貝葉斯模型”’
f = open(‘model.txt’)
scores = {}
for line in f:
word,counts = line.strip().rsplit(‘\t’,1)
scores[word] = eval(counts)
f.close()
return scores
def predict():
”’預測檔案的類標,標準輸入每一行為一個檔案”’
docCounts,features = loadFeatureWord()
docscores = [math.log(count * 1.0 /sum(docCounts)) for count in docCounts]
scores = loadModel()
rCount = 0
docCount = 0
for line in sys.stdin:
lable,text = line.strip().split(‘ ‘,1)
index = lable2id(lable[0])
words = text.split(‘ ‘)
preValues = list(docscores)
for word in words:
if word in features:
for i in xrange(len(preValues)):
preValues[i]+=math.log(scores[word][i])
m = max(preValues)
pIndex = preValues.index(m)
if pIndex == index:
rCount += 1
print lable,lables[pIndex],text
docCount += 1
print rCount,docCount,rCount * 1.0 / docCount
if __name__==”__main__”:
#shuffle()
#countForMI()
#trainBayes()
predict()
程式碼裡面,計算特徵詞與訓練模型、測試是分開的,需要修改main方法,比如計算特徵詞:
$cat train.txt | python bayes.py > feature.txt
訓練模型:
$cat train.txt | python bayes.py > model.txt
預測模型:
cat test.txt | python bayes.py > predict.out
總結
本文介紹了樸素貝葉斯分類方法,還以文字分類為例,給出了一個具體應用的例子,樸素貝葉斯的樸素體現在條件變數之間的獨立性假設,應用到文字分類上,作了兩個假設,一是各個特徵詞對分類的影響是獨立的,另一個是詞項在檔案中的順序是無關緊要的。樸素貝葉斯的獨立性假設在實際中並不成立,但在分類效上依然不錯,加上獨立性假設後,對與屬於類ck的謀篇檔案d,其p(ck|d)往往會估計過高,即本來預期p(ck|d)=0.55,而樸素貝葉斯卻計算得到p(ck|d)=0.99,但這並不影響分類結果,這是樸素貝葉斯分類器在文字分類上效果優於預期的原因。
參考文獻:
-
王斌 譯.資訊檢索導論. 人民郵電出版社
-
codemeals. 文字特徵選擇. cnblogs.
-
李航.統計學習方法.清華大學出版社
-
陳希孺. 機率論與數理統計.中國科學技術出版社
連結:cnblogs.com/fengfenggirl/p/classification_evaluate.html
親愛的讀者朋友們,您們有什麼想法,請點選【寫留言】按鈕,寫下您的留言。
資料人網(http://shujuren.org)誠邀各位資料人來平臺分享和傳播優質資料知識。
公眾號推薦:
好又樂書屋,專註分享有思想的人物,身心健康,自我教育,閱讀寫作和有趣味的生活等內容,傳播正能量。

閱讀原文,更多精彩!
分享是收穫,傳播是價值!
 知識星球
知識星球