本文長度為6500字,建議閱讀20分鐘
本文是Analytics Vidhya所舉辦的線上統計學測試的原題,有志於成為資料科學家或者資料分析師的同仁可以以這41個問題測試自己的統計學水平。
介紹
統計學是資料科學和任何資料分析的基礎。良好的統計學知識可以幫助資料分析師做出正確的商業決策。一方面,描述性統計幫助我們透過資料的集中趨勢和方差瞭解資料及其屬性。另一方面,推斷性統計幫助我們從給定的資料樣本中推斷總體的屬性。瞭解描述性和推斷性統計學知識對於立志成為資料科學家或分析師至關重要。
為了幫助您提高統計學知識,我們進行了這次實踐測試。測試涉及描述性和推斷性統計。測試題提供了答案和解釋,以防你遇到卡殼的問題。
如果您錯過了測試,請在閱讀答案之前嘗試解決問題。
總得分
以下是測試得分的分佈情況,幫助您評估您的測試表現。
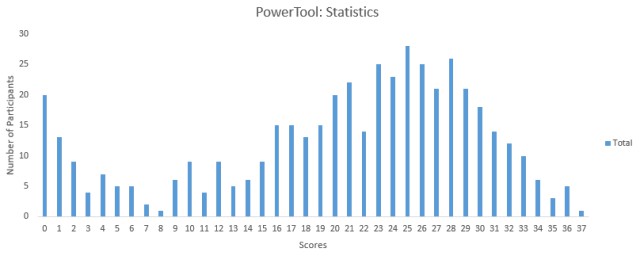
Mode Score:25
您可以訪問這裡(https://datahack.analyticsvidhya.com/contest/skilltest-statistics-3/lb)檢視最終成績。
超過450人參加了這次測試,獲得的最高分是37分。以下是一些關於分數分佈的統計資料:
-
平均得分:20.40
-
得分中位數:23
-
得分眾數:25
問題與答案
1)哪些統計方法用來度量資料的集中趨勢?
A)平均值和正態分佈
B)平均值,中位數和眾數
C)眾數,Alpha和極差
D)標準差,極差和平均值
E)中位數,極差和正態分佈
答案:(B)
平均值,中位數和眾數是分析資料集中趨勢的三種統計方法。 我們使用這些測量方法來查詢資料集的中心值,以及總結整個資料集。
2)給出5個數字:(5,10,15,5,15),求單項資料與平均值之間的離差的和。
A)10
B)25
C)50
D)0
E)以上都沒有
答案:(D)
單項資料的離差之和始終為0。
3)每年進行一次考試。 考試的平均分為150分,標準差為20。如果Ravi的Z值為1.50,他的得分是多少?
A)180
B)130
C)30
D)150
E)以上都沒有
答案:(A)
X =μ+Zσ,其中μ是平均值,σ是標準差,X是我們計算的分數。 因此X = 150 + 20 * 1.5 = 180
4)如果資料集中的單項數值發生變化,則以下集中趨勢中的哪個測量值一定會發生變化?
A)平均值
B)中位數
C)眾數
D)上述所有
答案:(A)
如果我們改動資料集中的任何值,資料集的平均值一定會改變。 因為平均值是由資料集中的所有值彙總求得的,所以資料集中的每個值都對平均值起作用。 中位數和眾數可能會改變,也可能不會隨資料集中的單個值而改變。
5)下圖所示,標尺的垂線上有六個資料點。

以下哪一條垂直線代表給定資料點的平均值?其中標尺的比例單位相同。
A)A
B)B
C)C
D)D
答案:(C)
從視覺上觀察資料點做判斷有點困難, 我們可以透過簡單的取值來理解平均值。 令A為1,B為2,C為3等。 所示的資料值將變為{1,1,1,4,5,6},這意味著是18/6 = 3即C.
6)如果正偏態分佈的中位數為50,則下列哪個選項是正確的?
A)平均值大於50
B)平均值小於50
C)眾數小於50
D)眾數大於50
E)A和C
F)B和D
答案:(E)
以下是負偏態分佈,正態分佈和正偏態分佈曲線:
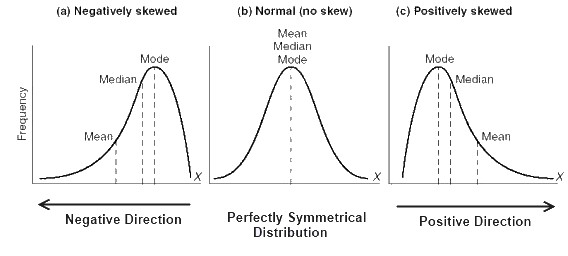
正如我們所看到的正偏態分佈的曲線,眾數
7)以下哪一項是下圖分佈的中位數的可能值?
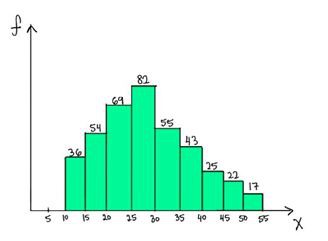
A)32
B)26
C)17
D)40
答案:(B)
為了回答這個問題,我們需要瞭解中位數的基本定義。 中位數是其前後值大約一半的值。 小於25的數值是(36 + 54 + 69 = 159),大於30的值的數量是(55 + 43 + 25 + 22 + 17 = 162)。 所以中位數應該在25到30之間。因此26是中位數的可能值。
8)計算樣本標準差時,下列哪項陳述對於貝塞爾校正(Bessel’s correction)是正確的?
1. 不論對樣本資料執行任何操作,都要使用貝塞爾校正。
2. 當我們嘗試用樣本估計總體的標準差時,使用貝塞爾校正。
3. 貝塞爾校正減少了標準差的偏差。
A)只有2
B)只有3
C)2和3
D)1和3
答案:(C)
與我們不應該總是做貝塞爾校正這個普遍觀點相反。 當我們用樣本的標準差來估算總體的標準差時,基本上是要做貝塞爾校正的。貝塞爾校正可以修正樣本的標準差使其更接近總體的情況。
9)如果公式中的分母使用(n-1)計算資料集的方差,則下列哪個選項正確?
A)資料集是一個樣本
B)資料集是一個總體
C)資料集可以是樣本或總體
D)資料集來自人口普查
E)以上都不正確
答案:(A)
如果公式中的方差分母使用了n-1,則表示該集合是樣本。 我們一般用離差的平方和除以n-1計算平均值,來估算總體的偏差。
當我們使用總體資料時,可以直接將離差的平方和除以n而不是n-1。
10)[對錯判斷]標準差可以為負值。
A)正確
B)錯誤
答案:(B)
以下是標準差的公式:

由於標準差是經過平方,累加,然後再開方,因此標準差不可能是負的。
11)標準差對異常值是否穩健?
A)是
B)否
答案:(B)
按照上面的標準差公式,可以發現過高或過低的值會增加標準差,儘管標準差與平均值非常不同。 因此,異常值將影響標準差。
12)對於下麵的正態分佈,以下哪個選項成立?
σ1,σ2和σ3分別表示曲線1,2和3的標準差。

A)σ1>σ2>σ3
B)σ1
C)σ1=σ2=σ3
D)以上皆否
答案:(B)
從正態分佈的定義來看,我們知道所有這3種形狀的曲線下的面積為1。 曲線3更平坦,因而更分散(大多數值在40-160之間),因此它的標準差最大。 類似地,曲線1的範圍非常窄,並且所有值都在80-120的小範圍內。 因此,曲線1的標準差最小。
13)在98%的置信區間,雙尾檢驗Z的臨界值是多少?
A)+/- 2.33
B)+/- 1.96
C)+/- 1.64
D)+/- 2.55
答案:(A)
我們需要檢視Z值表來回答這個問題。 對於雙尾檢驗和98%置信區間,我們應該檢查Z值之前的面積為0.99,因為平均值的左側和右側分別是1%。 因此,我們應該檢查區域 > 0.99的Z值。 該值為+/- 2.33。
14)[對錯判斷]標準正態分佈的曲線是對稱的,對稱軸為0,曲線下麵的面積為1。
A)正確
B)錯誤
答案:(A)
由正態分佈曲線的定義得知,曲線下麵的面積為1,對稱軸為零, 平均值、中位數和眾數都等於0。平均值左側的面積等於平均值右側的面積。 因此它是對稱的。
問題背景15-17
研究表明,在學習時聽音樂可以提高記憶力。 為了證明這一點,研究人員獲得了36名大學生的樣本,給他們做了一個標準記憶測試,同時聽一些背景音樂。 在正常情況下(沒有音樂),測試得到的平均分為25,標準偏差為6。實驗後樣本(有音樂)的平均分為28。
15)這種情況下的零假設是什麼?
A)學習時聽音樂不會影響記憶力。
B)學習時聽音樂可能會使記憶力退化。
C)在學習中聽音樂可能會提高記憶力。
D)在學習期間聽音樂不會提高記憶力,還可能會使記憶力變得更糟。
答案:(D)
零假設通常是假設宣告,測量現象彼此之間沒有關係。 這裡的零假設是聽音樂和記憶力的提高之間沒有關係。
16)什麼是第一類錯誤?
A)學習時聽音樂可以提高記憶力,且該結論正確。
B)學習時聽音樂可以提高記憶力,但實際上記憶力並沒有提高。
C)學習時聽音樂不會提高記憶力,但實際上記憶力提高了。
答案:(B)
第一類錯誤意味著當假設的結論實際上為真時,我們卻拒絕了零假設。 這裡的零假設是音樂不會提高記憶力。 第一類錯誤是我們拒絕了零假設,也就是說結論顯示音樂提高了記憶力,但實際上它並沒有提高記憶力。
17)執行Z檢驗後,我們可以得出什麼結論?
A)聽音樂不會提高記憶力。
B)聽音樂會顯著提高記憶力。
C)資訊不足以作任何結論。
D)以上都不對
答案:(B)
我們在給定的情況下進行Z檢驗。 我們知道零假設是聽音樂不會提高記憶力。
備擇假設是聽音樂確實提高了記憶力。
在這種情況下,標準誤差即:

來自這個總體的樣本的平均值為28的Z值得分為:

從Z值表中可以看出,α= 0.05(單尾)的Z臨界值為1.65。
因此,由於觀察到的Z值大於Z臨界值,所以我們可以拒絕零假設,可以下結論說聽音樂確實改善了記憶力,置信度是95%。
18)研究者從他的分析中得出結論:安慰劑治療了艾滋病。 他犯了哪一類的錯誤?
A)第一類錯誤
B)第二類錯誤
C)以上都不是。 研究人員沒有發生錯誤。
D)不能確定
答案:(D)
根據定義,第一類錯誤是假設實際是真時,拒絕零假設;第二類錯誤是假設實際是假時,接受零假設。 在這種情況下定義錯誤,我們需要首先定義零假設和備擇假設。
19)當我們往資料中引入一些異常值時,置信區間會發生什麼變化?
A)置信區間對異常值是穩健的
B)置信區間隨著異常值的引入而增加。
C)隨著異常值的引入,置信區間將減少。
D)在這種情況下,我們無法確定置信區間。
答案:(B)
我們知道置信區間取決於資料的標準差。 如果我們將異常值引入資料,則標準差增加,因此置信區間也增加。
問題背景20-22
醫生想透過控制飲食來降低所有患者的血糖水平。 他發現所有患者的血糖含量平均值為180,標準差為18。然後有9名患者開始控制飲食,他觀察到樣本的平均值為175。現在,他正在考慮建議讓他的所有患者都去控制飲食。
備註:置信區間99%。
20)平均值的標準誤差是多少?
A)9
B)6
C)7.5
D)18
答案:(B)
平均值的標準誤差是標準差除以樣本量的平方根。即:

21)當所有患者都開始控制飲食後,血糖平均值降至175以下的機率是多少?
A)20%
B) 25%
C)15%
D)12%
答案:(A)
這個問題需要計算出幹預後所有患者的平均血糖值為175的機率, 可以透過給定的平均值計算出Z值。

查Z值表,得到Z對應的數值 = -0.833〜0.2033。
因此,如果每個人都開始控制飲食,那麼所有患者平均血糖值降至175的機率大約為20%。
22)以下哪項陳述是正確的?
A)醫生有有效的證據證明控制飲食可以降低血糖水平。
B)醫生沒有足夠的證據證明控制飲食能夠降低血糖水平。
C)如果醫生用同樣的方法讓所有患者控制飲食,那麼平均血糖將會降至160以下。
答案:(B)
我們需要核實是否有足夠的證據來拒絕零假設。 零假設是控制飲食對血糖沒有影響。 這是一個雙尾檢驗。 雙尾檢驗的Z臨界值為±2.58。
我們計算出的Z值是-0.833。
由於Z值 < Z臨界值,因此我們沒有足夠的證據證明控制飲食能夠降低血糖。
問題背景23-25
一位研究人員正在試圖檢驗兩種不同教學方法的效果。 他把20名學生分成兩組,每組10人。 對於第1組,教學方法是使用有趣的例子。 對於第2組,教學方法是使用軟體來幫助學生學習。 兩組學生經過20分鐘的授課後,所有學生進行了考試。
我們想計算兩組學生的考試得分是否有顯著的差異。
已知如下資訊:
• α= 0.05,雙尾檢驗。
• 第1組的測試平均分數= 10
• 第2組的測試平均分數= 7
• 標準誤差= 0.94
23) t-統計量的值是什麼?
A)3.191
B) 3.395
C)不能確定
D)以上都不是
答案:(A)
t統計量是指兩組之間相差多少個標準誤差。
=(10-7)/ 0.94 = 3.191
24)兩組的考試得分是否有顯著差異?
A)有
B)沒有
答案:(A)
零假設是兩組之間沒有差異,而被擇假設是兩組之間有顯著差異。
在α= 0.05條件下的雙尾檢驗的t臨界值為±2.101。 得到t統計量為3.191。 由於t統計量大於t臨界值,因此我們可以拒絕零假設,認為這兩組在95%的置信區間上有顯著差異。
25) 考試得分的變異性在多大比例上可由教學方法不同來解釋?
A) 36.13
B) 45.21
C) 40.33
D) 32.97
答案:(A)
R2的值給出了分數變異性的百分比。R2的公式如下:

在本題中,自由度是10 + 10 -2,因為兩組各有10人,所以自由度是18。

26)[對錯判斷] F統計量不能為負。
A)正確
B)錯誤
答案:(A)
F統計量是我們對不同組進行方差分析,瞭解不同組之間的差異時得到的值。 F統計量是組間變異與組內變異的比值。
下麵是F統計量的公式:

由於分子和分母具有平方項,因此F統計量不能為負。
27)下列哪張圖具有很強的正相關性?

答案:(B)
強正相關需要滿足下列條件:如果x增加,y也增加;如果x減少,y也減小。 在這種情況下,線的斜率為正,資料點將顯示出明確的線性關係。 選項B顯示出很強的正相關關係。
28)兩個變數(Var1和Var2)之間的相關性為0.65。 如果給Var1中的所有值加上2後,相關係數將會_______?
A)增加
B)減少
C)以上都沒有
答案:(C)
任一變數增加或減去一個恆定值,相關係數將保持不變。相關性的計算公式可以很容易地幫助我們理解這一點。

如果我們給變數的所有值都加上一個常數值,則這個變數將發生相同的變化量,變數的差異將保持不變。 因此,相關係數不會變化。
29)據觀察發現,數學考試成績與在學生在考試當天進行體育運動存在非常高的相關性。 你能從中推斷出什麼結論?
1. 高度相關意味著運動後考試成績會很高。
2. 相關性並不意味著因果關係。
3. 相關性衡量了運動量與考試成績之間的線性關係的強度。
A)只有1
B)1和3
C)2和3
D) 以上陳述都對
答案:(C)
雖然有時直覺上強相關性就表明因果關係,但實際上相關性並不意味著任何的因果推論。 它只是告訴我們兩個變數之間的關係的強度。 如果這兩個變數同時改變,那麼它們之間存在高度的相關性。
30)如果數學考試成績與體育運動之間的相關係數(r)是0.86,那麼用體育運動來解釋數學考試成績的變異性的百分比是多少?
A)86%
B)74%
C)14%
D)26%
答案:(B)
變異性的百分比R2由相關係數的平方得到, 該比值可以解釋由一個變數引起另一個變數變異的比例。 因此,用運動解釋數學考試成績的變異性為0.862。
31)下列選項對於直方圖的描述,哪個是正確的?

A)上述直方圖是單峰的
B)上述直方圖是雙峰的
C)上述給出的不是直方圖
D)以上都不對
答案:(B)
上述直方圖是雙峰的。 我們可以看到直方圖有兩個峰值,表示有兩個高頻。
32)考慮回歸直線方程y = ax + b,其中a是斜率,b是截距。 如果我們知道斜率的值,那麼透過下列哪個選項,我們一定可以找到截距的值?
A)把值(0, 0)代入到回歸直線方程中
B)代入回歸擬合線上任意一點的值,計算b的值
C)使用方程中的x和y的平均值,和a一起計算得到b
D)以上都不對
答案:(C)
使用普通最小二乘回歸法的直線始終透過x和y的平均值。 如果我們知道線上的任意一個點和斜率的值,就可以很容易地找到截距。
33)當我們向線性回歸模型引入更多的變數時會發生什麼?
A)R2可能增加或保持不變,調整後的R2可能增加也可能減少。
B)R2可能增加也可能減少,但調整後的R2總是增加。
C)當為模型引入新的變數時,R2和調整後的R2總是增加。
D)R2和調整後的R2都有可能增加或減少,依賴於引入的變數。
答案:(A)
R2總是增加或至少保持不變,因為使用普通最小二乘法,向模型新增更多的變數,方差的總和不會增加,R2也沒有減少。調整後的R2是在模型中根據預測變數的數量進行調整後,R2的修改版本。只有當新的預測變數改進了模型且超過預期時,調整後的R2才會增加。當預測變數對模型的改進低於預期時,調整後的R2將減少。
34)在散點圖中,回歸線上面或下麵的點到回歸線的垂直距離稱為____?

A)殘差
B)預測誤差
C)預測
D)A和B
E)以上都不是
答案:(D)
我們從圖中看到的線是從回歸線到點的垂直距離, 這些距離被稱為殘差或預測誤差。
35)在最小二乘法的一元線性回歸方程中,相關係數與決定繫數之間的關係是?
A)兩者無關
B)決定繫數是相關係數的平方
C)決定繫數是相關係數的平方根
D) 兩者都是相同的
答案:(B)
決定繫數是R2,告訴我們自變數解釋因變數的變異程度,也是相關係數的平方。 在多元回歸的情況下,R2也可表示成解釋方差之和與方差總和的比值。
36)顯著性水平與置信度之間的關係是什麼?
A)顯著性水平=置信度
B)顯著性水平= 1-置信度
C)顯著性水平= 1 /置信度
D)顯著性水平= sqrt(1 – 置信度)
答案:(B)
顯著性水平就是1-置信度。 如果顯著性水平為0.05,那麼相應的置信度為95%或0.95。顯著性水平就是當零假設為真時,獲得極端值或超過極端值的結果的機率。 置信區間是總體引數可能值的範圍,如總體平均值。 例如,如果你在95%的置信區間內計算出冰淇淋的平均價格,那麼說明你有95%的信心認為這個平均價格包含了所有冰淇淋的真實平均價格。
顯著性水平和置信度在正態分佈中是互補的。
37)[對錯判斷] 假設給定一個變數V以及其平均值和中位數。 基於這些值,你可以判斷出變數“V”是有偏的。
平均值(V)>中位數(V)
A)正確
B)錯誤
答案:(B)
因為沒有提到變數V的分佈型別,我們不能肯定地說V是有偏的。
38)普通最小二乘法(OLS)線性回歸方程得到的回歸線試圖____?
A)透過盡可能多的點
B)透過盡可能少的點
C)最小化所觸及的點數
D)最小化點到回歸線的距離的平方
答案:(D)
回歸線嘗試最小化點到回歸線之間的距離的平方。根據定義,普通最小二乘法回歸方程具有誤差的平方的最小和。 這意味著殘差的平方和也應該是最小化的。這條回歸線可能會也可能不會透過最多的資料點。最常見的情況是,當資料有很多離群值或線性關係不是非常強的時候,回歸線不是透過所有的點,而是儘量減少透過的點的誤差平方和。
39)下表是一個線性回歸方程(Y = 5X+40)。

以下哪一項是該線性方程模型的MAE(平均絕對誤差)?
A)8.4
B)10.29
C)42.5
D)以上都不是
答案:(A)
為了計算本題中的平均絕對誤差,我們首先用給定的方程計算Y值,然後計算相對於實際Y值的絕對誤差。 那麼這個絕對誤差的平均值將是平均絕對誤差。 下表總結了這些值。
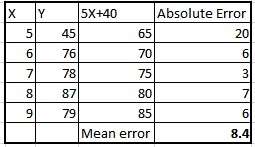
40)對體重(y)和身高(x)進行回歸分析得出以下最小二乘直線:y = 120 + 5x。 這意味著如果身高增加1英寸,則預期的體重將?
A)增加1磅
B)增加5磅
C)增加125磅
D)以上都不是
答案:(B)
觀察給定方程y = 120 + 5x, 如果身高增加1個單位,則體重將增加5磅。因為截距120是不變的,不會貢獻差異。
41)[對錯判斷] 皮爾森(Pearson)相關性捕捉了兩個變數之間的線性依賴關係,而斯皮爾曼(Spearman)相關性捕捉的是兩個變數之間的單調相關關係。
A)正確
B)錯誤
答案:(A)
該表述正確。皮爾森(Pearson)相關性評估了兩個連續變數之間的線性相關關係。 當一個變數的變化與另一個變數的變化成比例時,相關關係是線性的。
而斯皮爾曼(Spearman)相關性是評價單調相關關係。 單調相關關係是兩個變數共同變化,但是不一定以固定的比例變化。
寫在最後
希望你能從解答問題中發現樂趣,雖然有時候這些問題可能會讓你抓狂。如果你對於上述問題有什麼想法或者反饋,歡迎與我們分享。
我們很樂意將你的想法納入到接下來的文章和測試中。此外,一個問題可能有多種解答方法,上面的解答可能只是其中的一種。我們儘量詳細地闡述解答思路,但是如果仍有疑問或者想進一步探討的話,請在下麵的評論中留言。
原文連結:
https://www.analyticsvidhya.com/blog/2017/05/41-questions-on-statisitics-data-scientists-analysts/
END
作者:Dishashree Gupta;翻譯:閔黎 盧苗苗;校對:丁楠雅;
作者介紹:
閔黎:惠普企業,資深專案經理,負責全球運營資料分析,視覺化輔助決策,最佳化運營,推動企業內部改進。探索大資料的神秘原力,顛覆式創新是我的興趣所在。
盧苗苗:北京語言大學英語專業在讀。一個帶有理科思維的文科生。 愛思考善分析,腦洞大想法多,喜歡在複雜事物中發現潛在聯絡。既喜歡仰望星空,也喜歡腳踏實地。作為資料派的活躍分子,希望能同各位大們好好學習。
本文轉自:資料派THU 公眾號;

關聯閱讀
原創系列文章:
資料運營 關聯文章閱讀:
資料分析、資料產品 關聯文章閱讀:
80%的運營註定了打雜?因為你沒有搭建出一套有效的使用者運營體系
商務合作|約稿 請加qq:365242293
更多相關知識請回覆:“ 月光寶盒 ”;
資料分析(ID : ecshujufenxi )網際網路科技與資料圈自己的微信,也是WeMedia自媒體聯盟成員之一,WeMedia聯盟改寫5000萬人群。

 知識星球
知識星球