導讀:為什麼正態分佈如此特殊?為什麼大量資料科學和機器學習的文章都圍繞正態分佈進行討論?我決定寫一篇文章,用一種簡單易懂的方式來介紹正態分佈。
在機器學習的世界中,以機率分佈為核心的研究大都聚焦於正態分佈。本文將闡述正態分佈的機率,並解釋它的應用為何如此的廣泛,尤其是在資料科學和機器學習領域,它幾乎無處不在。
我將會從基礎概念出發,解釋有關正態分佈的一切,並揭示它為何如此重要。
作者:Farhad Malik 譯者:Monanfei 來源:AI科技大本營(ID: rgznai100)
▲1893年人類身高分佈圖,作者:Alphonse Bertillon
本文的主要內容如下:
機率分佈是什麼 正態分佈意味著什麼 正態分佈的變數有哪些 如何使用 Python 來檢驗資料的分佈 如何使用 Python 引數化生產一個正態分佈 正態分佈的問題 01 簡短的背景介紹 首先,正態分佈又名高斯分佈 它以數學天才 Carl Friedrich Gauss 命名 正態分佈又名高斯分佈 越簡單的模型越是常用,因為它們能夠被很好的解釋和理解。正態分佈非常簡單,這就是它是如此的常用的原因。 因此,理解正態分佈非常有必要。 02 什麼是機率分佈?
首先介紹一下相關概念。
考慮一個預測模型,該模型可以是我們的資料科學研究中的一個元件。
如果我們想精確預測一個變數的值,那麼我們首先要做的就是理解該變數的潛在特性。 首先我們要知道該變數的可能取值,還要知道這些值是連續的還是離散的。簡單來講,如果我們要預測一個骰子的取值,那麼第一步就是明白它的取值是1 到 6(離散)。 第二步就是確定每個可能取值(事件)發生的機率。如果某個取值永遠都不會出現,那麼該值的機率就是 0 。 事件的機率越大,該事件越容易出現。 在實際操作中,我們可以大量重覆進行某個實驗,並記錄該實驗對應的輸出變數的結果。 我們可以將這些取值分為不同的集合類,在每一類中,我們記錄屬於該類結果的次數。例如,我們可以投10000次骰子,每次都有6種可能的取值,我們可以將類別數設為6,然後我們就可以開始對每一類出現的次數進行計數了。 我們可以畫出上述結果的曲線,該曲線就是機率分佈曲線。標的變數每個取值的可能性就由其機率分佈決定。 一旦我們知道了變數的機率分佈,我們就可以開始估計事件出現的機率了,我們甚至可以使用一些機率公式。至此,我們就可更好的理解變數的特性了。機率分佈取決於樣本的一些特徵,例如平均值,標準偏差,偏度和峰度。 如果將所有機率值求和,那麼求和結果將會是100%
世界上存在著很多不同的機率分佈,而最廣泛使用的就是正態分佈了。 03 初遇正態分佈
我們可以畫出正態分佈的機率分佈曲線,可以看到該曲線是一個鐘型的曲線。如果變數的均值,模和中值相等,那麼該變數就呈現正態分佈。
如下圖所示,為正態分佈的機率分佈曲線:
理解和估計變數的機率分佈非常重要。 下麵列出的變數的分佈都比較接近正態分佈:
人群的身高 成年人的血壓 傳播中的粒子的位置 測量誤差 回歸中的殘差 人群的鞋碼 一天中僱員回家的總耗時 教育指標
此外,生活中有大量的變數都是具有 x % 置信度的正態變數,其中,x<100。
04 什麼是正態分佈?
正態分佈只依賴於資料集的兩個特徵:樣本的均值和方差。
均值——樣本所有取值的平均 方差——該指標衡量了樣本總體偏離均值的程度
正態分佈的這種統計特性使得問題變得異常簡單,任何具有正態分佈的變數,都可以進行高精度分預測。 值得註意的是,大自然中發現的變數,大多近似服從正態分佈。
正態分佈很容易解釋,這是因為:
正態分佈的均值,模和中位數是相等的。 我們只需要用均值和標準差就能解釋整個分佈。
正態分佈是我們熟悉的正常行為。
05 為何如此多的變數都大致服從正態分佈?
這個現象可以由如下定理解釋:當在大量隨機變數上重覆很多次實驗時,它們的分佈總和將非常接近正態分佈。
由於人的身高是一個隨機變數,並且基於其他隨機變數,例如一個人消耗的營養量,他們所處的環境,他們的遺傳等等,這些變數的分佈總和最終是非常接近正態的。
這就是中心極限定理。
本文的核心:
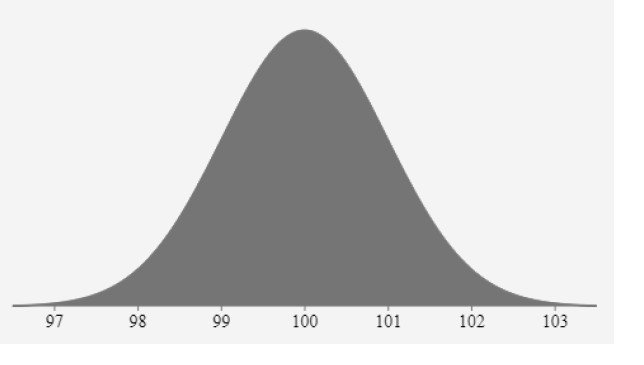
我們從上文的分析得出,正態分佈是許多隨機分佈的總和。如果我們繪製正態分佈密度函式,那麼它的曲線將具有以下特徵:
如上圖所示,該鐘形曲線有均值為 100,標準差為1:
均值是曲線的中心。這是曲線的最高點,因為大多數點都是均值。 曲線兩側的點數相等。曲線的中心具有最多的點數。 曲線下的總面積是變數所有取值的總機率。 因此總曲線面積為 100% 更進一步,如上圖所示:
約 68.2% 的點在 -1 到 1 個標準偏差範圍內。 約 95.5% 的點在 -2 到 2 個標準偏差範圍內。 約 99.7% 的點在 -3 至 3 個標準偏差範圍內。
這使我們可以輕鬆估計變數的變化性,並給出相應置信水平,它的可能取值是多少。例如,在上面的灰色鐘形曲線中,變數值在 99-101 之間的可能性為 68.2%。 06 正態機率分佈函式 正態機率分佈函式的形式如下:
機率密度函式基本上可以看作是連續隨機變數取值的機率。
正態分佈是鐘形曲線,其中mean = mode = median。 如果使用機率密度函式繪製變數的機率分佈曲線,則給定範圍的曲線下的面積,表示標的變數在該範圍內取值的機率。 機率分佈曲線基於機率分佈函式,而機率分佈函式本身是根據諸如平均值或標準差等多個引數計算的。 我們可以使用機率分佈函式來查詢隨機變數取值範圍內的值的相對機率。例如,我們可以記錄股票的每日收益,將它們分組到適當的集合類中,然後計算股票在未來獲得20-40%收益的機率。
標準差越大,樣品中的變化性越大。
07 如何使用 Python 探索變數的機率分佈
最簡單的方法是載入 data frame 中的所有特徵,然後執行以下指令碼(使用pandas 庫): 該函式向我們展示了所有變數的機率分佈。
08 變數服從正態分佈意味著什麼?
如果我們將大量具有不同分佈的隨機變數加起來,所得到的新變數將最終具有正態分佈。這就是前文所述的中心極限定理。
服從正態分佈的變數總是服從正態分佈。例如,假設 A 和 B 是兩個具有正態分佈的變數,那麼:
A x B 是正態分佈 A + B 是正態分佈
因此,使用正態分佈,預測變數併在一定範圍內找到它的機率會變得非常簡單。
09 樣本不服從正態分佈怎麼辦?
我們可以將變數的分佈轉換為正態分佈。
我們有多種方法將非正態分佈轉化為正態分佈:
1. 線性變換
一旦我們收集到變數的樣本資料,我們就可以對樣本進行線性變化,並計算Z得分:
計算平均值 計算標準偏差 對於每個 x,使用以下方法計算 Z:
2. 使用 Boxcox 變換
我們可以使用 SciPy 包將資料轉換為正態分佈: 3. 使用 Yeo-Johnson 變換 另外,我們可以使用 yeo-johnson 變換。Python 的 sci-kit learn 庫提供了相應的功能: 10 正態分佈的問題 由於正態分佈簡單且易於理解,因此它也在預測研究中被過度使用。假設變數服從正態分佈會有一些顯而易見的缺陷。例如,我們不能假設股票價格服從正態分佈,因為價格不能為負。因此,我們可以假設股票價格服從對數正態分佈,以確保它永遠不會低於零。
我們知道股票收益可能是負數,因此收益可以假設服從正態分佈。 假設變數服從正態分佈而不進行任何分析是愚蠢的。 變數可以服從Poisson,Student-t 或 Binomial 分佈,盲目地假設變數服從正態分佈可能導致不準確的結果。 11 總結
本文闡述了正態分佈的概念和性質,以及它如此重要的原因。
希望能幫助到你。
原文連結:http://bit.ly/2NyetFz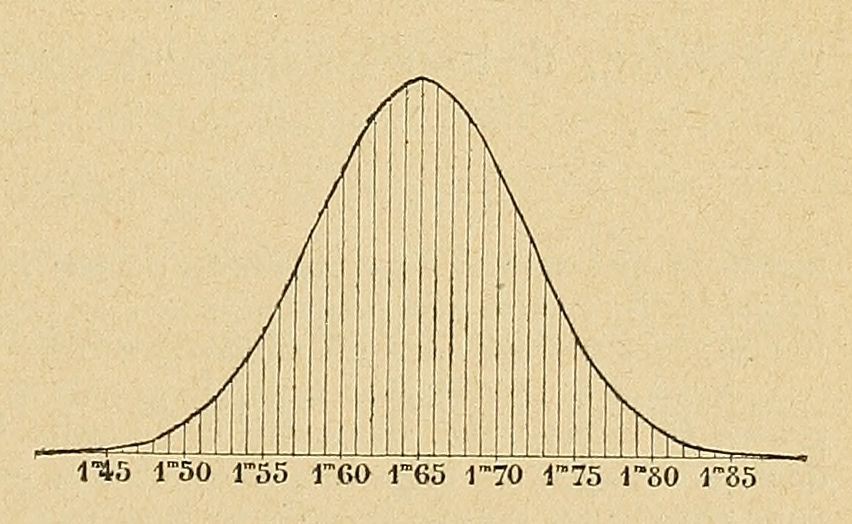

DataFrame.hist(bins=10)
#Make a histogram of the DataFrame.

scipy.stats.boxcox(x, lmbda=None, alpha=None)
sklearn.preprocessing.PowerTransformer(method=’yeojohnson’,standardize=True, copy=True)
歡迎光臨
每天分享高質量文章
每天分享高質量文章
 知識星球
知識星球
朋友會在“發現-看一看”看到你“在看”的內容