本文經機器之心(微信公眾號:almosthuman2014)授權轉載,禁止二次轉載
選自Medium,作者:Harisankar Haridas
機器之心編譯,參與:陳韻竹、思源
原文:https://towardsdatascience.com/deep-neural-network-implemented-in-pure-sql-over-bigquery-f3ed245814d3
我們熟知的SQL是一種資料庫查詢陳述句,它方便了開發者在大型資料中執行高效的操作。但本文從另一角度巢狀SQL查詢陳述句而構建了一個簡單的三層全連線網路,雖然由於陳述句的巢狀過深而不能高效計算,但仍然是一個非常有意思的實驗。

在這篇文章中,我們將純粹用SQL實現含有一個隱藏層(以及帶 ReLU 和 softmax 啟用函式)的神經網路。這些神經網路訓練的步驟包含前向傳播和反向傳播,將在 BigQuery 的單個SQL查詢陳述句中實現。當它在 BigQuery 中執行時,實際上我們正在成百上千臺伺服器上進行分散式神經網路訓練。聽上去很贊,對吧?
也就是說,這個有趣的專案用於測試 SQL 和 BigQuery 的限制,同時從宣告性資料的角度看待神經網路訓練。這個專案沒有考慮任何的實際應用,不過最後我將討論一些實際的研究意義。
我們先從一個基於神經網路的簡單分類器開始。它的輸入尺寸為 2,輸出為二分類。我們將有一個維度為 2 的單隱層和 ReLU 啟用函式。輸出層的二分類將使用 softmax 函式。我們在實現網路時遵循的步驟將是在 Karpathy’s CS231n 指南(https://cs231n.github.io/neural-networks-case-study/)中展示的基於 SQL 版本的 Python 示例。
模型
該模型含有以下引數:
輸入到隱藏層
-
W: 2×2 的權重矩陣(元素: w_00, w_01, w_10, w_11)
-
B: 2×1 的偏置向量(元素:b_0, b_1)
隱藏到輸出層
-
W2: 2×2 的權重矩陣(元素: w2_00, w2_01, w2_10, w2_11)
-
B2: 2×1 的偏置向量(元素:b2_0, b2_1)
訓練資料儲存在 BigQuery 表格當中,列 x1 和 x2 的輸入和輸出如下所示(表格名稱:example_project.example_dataset.example_table)
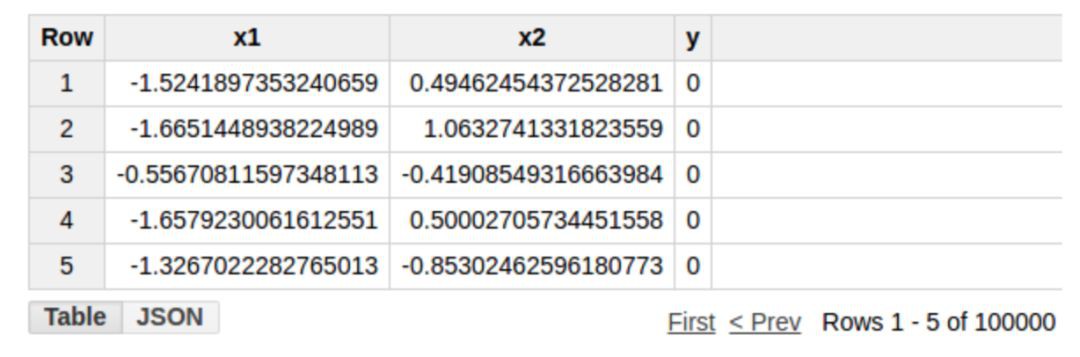
如前所述,我們將整個訓練作為單個 SQL 查詢陳述句來實現。在訓練完成後,透過 SQL 查詢陳述句將會傳回引數的值。正如你可能猜到的,這將是一個層層巢狀的查詢,我們將逐步構建以準備這個查詢陳述句。我們將會從最內層的子查詢開始,然後逐個增加巢狀的外層。
前向傳播
首先,我們將權重引數 W 和 W2 設為服從正態分佈的隨機值,將權重引數 B 和 B2 設定為 0。 W 和 W2 的隨機值可以透過 SQL 本身產生。為了簡單起見,我們將從外部生成這些值併在 SQL 查詢中使用。用於初始化引數的內部子查詢如下:
SELECT *,
-0.00569693 AS w_00,
0.00186517 AS w_01,
0.00414431 AS w_10,
0.0105101 AS w_11,
0.0 AS b_0,
0.0 AS b_1,
-0.01312284 AS w2_00,
-0.01269512 AS w2_01,
0.00379152 AS w2_10,
-0.01218354 AS w2_11,
0.0 AS b2_0,
0.0 AS b2_1
FROM `example_project.example_dataset.example_table`
請註意,表格 example_project.example_dataset.example_table 已經包含了列 x1、 x2 和 y。模型引數將會被作為上述查詢結果的附加列新增。
接下來,我們將計算隱藏層的啟用值。我們將使用含有元素 d0 和 d1 的向量 D 表示隱藏層。我們需要執行矩陣操作 D = np.maximum(0, np.dot(X, W) + B),其中 X 表示輸入向量(元素 x1 和 x2)。這個矩陣運算包括將權重 W 和輸入 X 相乘,再加上偏置向量 B。然後,結果將被傳遞給非線性 ReLU 啟用函式,該函式將會把負值設定為 0。SQL 中的等效查詢為:
SELECT *,
(CASE
WHEN ((x1*w_00 + x2*w_10) + b_0) > 0.0 THEN ((x1*w_00 + x2*w_10) + b_0)
ELSE 0.0
END) AS d0,
(CASE
WHEN ((x1*w_01 + x2*w_11) + b_0) > 0.0 THEN ((x1*w_01 + x2*w_11) + b_1)
ELSE 0.0
END) AS d1
FROM {inner subquery}
上面的查詢將兩個新列 d0 和 d1 新增到之前內部子查詢的結果當中。 上述查詢的輸出如下所示。

這完成了從輸入層到隱藏層的一次轉換。現在,我們可以執行從隱藏層到輸出層的轉換了。
首先,我們將計算輸出層的值。公式是:scores = np.dot(D, W2) + B2。然後,我們將對計算出來的值用 softmax 函式來獲得每個類的預測機率。SQL 內部的等價子查詢如下:
SELECT *,
EXP(scores_0)/(EXP(scores_0) + EXP(scores_1)) AS probs_0,
EXP(scores_1)/(EXP(scores_0) + EXP(scores_1)) AS probs_1
FROM
( SELECT *,
((d0*w2_00 + d1*w2_10) + b2_0) AS scores_0,
((d0*w2_01 + d1*w2_11) + b2_1) AS scores_1
FROM {INNER sub-query})
首先,我們將使用交叉熵損失函式來計算當前預測的總損失。首先,計算每個樣本中正確類預測機率對數的負值。交叉熵損失只是這些 X 和 Y 實體中數值的平均值。自然對數是一個遞增函式,因此,將損失函式定義為負的正確類預測機率對數很直觀。如果正確類的預測機率很高,損失函式將會很低。相反,如果正確類的預測機率很低,則損失函式值將很高。
為了減少過擬合的風險,我們也將同樣增加 L2 正則化。在整體損失函式中,我們將包含 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2),其中 reg 是超引數。在損失函式中包括這一函式將會懲罰那些權重向量中較大的值。
在查詢當中,我們同樣會計算訓練樣本的數量(num_examples)。這對於後續我們計算平均值來說很有用。SQL 查詢中計算整體損失函式的陳述句如下:
SELECT *,
(sum_correct_logprobs/num_examples) + 1e-3*(0.5*(w_00*w_00 + w_01*w_01 + w_10*w_10 + w_11*w_11) + 0.5*(w2_00*w2_00 + w2_01*w2_01 + w2_10*w2_10 + w2_11*w2_11)) AS loss
FROM
(SELECT *,
SUM(correct_logprobs) OVER () sum_correct_logprobs,
COUNT(1) OVER () num_examples
FROM
(SELECT *,
(CASE
WHEN y = 0 THEN -1*LOG(probs_0)
ELSE -1*LOG(probs_1)
END) AS correct_logprobs
FROM {inner subquery}))反向傳播
接下來,對於反向傳播,我們將計算每個引數對於損失函式的偏導數。我們使用鏈式法則從最後一層開始逐層計算。首先,我們將透過使用交叉熵和 softmax 函式的導數來計算 score 的梯度。與此相對的查詢是:
SELECT *,
(CASE
WHEN y = 0 THEN (probs_0–1)/num_examples
ELSE probs_0/num_examples
END) AS dscores_0,
(CASE
WHEN y = 1 THEN (probs_1–1)/num_examples
ELSE probs_1/num_examples
END) AS dscores_1
FROM {inner subquery}
在上文中,我們用 scores = np.dot(D, W2) + B2 算出了分數。因此,基於分數的偏導數,我們可以計算隱藏層 D 和引數 W2,B2 的梯度。對應的查詢陳述句是:
SELECT *,
SUM(d0*dscores_0) OVER () AS dw2_00,
SUM(d0*dscores_1) OVER () AS dw2_01,
SUM(d1*dscores_0) OVER () AS dw2_10,
SUM(d1*dscores_1) OVER () AS dw2_11,
SUM(dscores_0) OVER () AS db2_0,
SUM(dscores_1) OVER () AS db2_1,
CASE
WHEN (d0) <= 0.0 THEN 0.0
ELSE (dscores_0*w2_00 + dscores_1*w2_01)
END AS dhidden_0,
CASE
WHEN (d1) <= 0.0 THEN 0.0
ELSE (dscores_0*w2_10 + dscores_1*w2_11)
END AS dhidden_1
FROM {inner subquery}
同理,我們知道 D = np.maximum(0, np.dot(X, W) + B)。因此,透過 D 的偏導,我們可以計算出 W 和 B 的導數。我們無須計算 X 的偏導,因為它不是模型的引數,且也不必透過其它模型引數進行計算。計算 W 和 B 的偏導的查詢陳述句如下:
SELECT *,
SUM(x1*dhidden_0) OVER () AS dw_00,
SUM(x1*dhidden_1) OVER () AS dw_01,
SUM(x2*dhidden_0) OVER () AS dw_10,
SUM(x2*dhidden_1) OVER () AS dw_11,
SUM(dhidden_0) OVER () AS db_0,
SUM(dhidden_1) OVER () AS db_1
FROM {inner subquery}
最後,我們使用 W、B、W2 及 B2 各自的導數進行更新操作。計算公式是 param = learning_rate * d_param ,其中learning_rate 是引數。為了體現 L2 正則化,我們會在計算 dW 和 dW2 時加入一個正則項 reg*weight。我們也去掉如 dw_00, correct_logprobs 等快取的列,它們曾在子查詢時被建立,用於儲存訓練資料(x1, x2 及 y 列) 和模型引數(權重和偏置項)。對應的查詢陳述句如下:
SELECT x1,
x2,
y,
w_00 — (2.0)*(dw_00+(1e-3)*w_00) AS w_00,
w_01 — (2.0)*(dw_01+(1e-3)*w_01) AS w_01,
w_10 — (2.0)*(dw_10+(1e-3)*w_10) AS w_10,
w_11 — (2.0)*(dw_11+(1e-3)*w_11) AS w_11,
b_0 — (2.0)*db_0 AS b_0,
b_1 — (2.0)*db_1 AS b_1,
w2_00 — (2.0)*(dw2_00+(1e-3)*w2_00) AS w2_00,
w2_01 — (2.0)*(dw2_01+(1e-3)*w2_01) AS w2_01,
w2_10 — (2.0)*(dw2_10+(1e-3)*w2_10) AS w2_10,
w2_11 — (2.0)*(dw2_11+(1e-3)*w2_11) AS w2_11,
b2_0 — (2.0)*db2_0 AS b2_0,
b2_1 — (2.0)*db2_1 AS b2_1
FROM {inner subquery}
這包含了正向和反向傳播的一整個迭代過程。以上查詢陳述句將傳回更新後的權重和偏置項。部分結果如下所示:
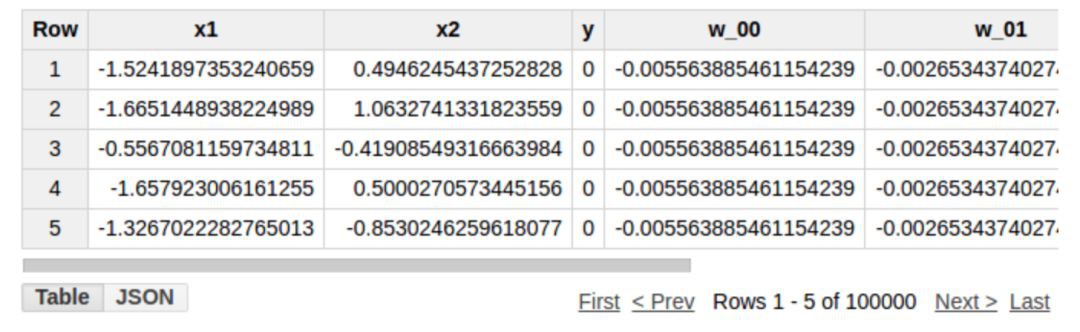
為了進行多次訓練迭代,我們將反覆執行上述過程。用一個簡單 Python 函式足以搞定,程式碼連結如下:https://github.com/harisankarh/nn-sql-bq/blob/master/training.py。
因為迭代次數太多,查詢陳述句巢狀嚴重。執行 10 次訓練迭代的查詢陳述句地址如下:
https://github.com/harisankarh/nn-sql-bq/blob/master/out.txt
因為查詢陳述句的多重巢狀和複雜度,在 BigQuery 中執行查詢時多項系統資源告急。BigQuery 的標準 SQL 擴充套件的縮放性比傳統 SQL 語言要好。即使是標準 SQL 查詢,對於有 100k 個實體的資料集,也很難執行超過 10 個迭代。因為資源的限制,我們將會使用一個簡單的決策邊界來評估模型,如此一來,我們就可以在少量迭代後得到較好的準確率。
我們將使用一個簡單的資料集,其輸入 X1、X2 服從標準正態分佈。二進位制輸出 y 簡單判斷 x1 + x2 是否大於 0。為了更快的訓練完 10 個迭代,我們使用一個較大的學習率 2.0(註意:這麼大的學習率並不推薦實際使用,可能會導致發散)。將上述陳述句執行 10 個迭代得出的模型引數如下:
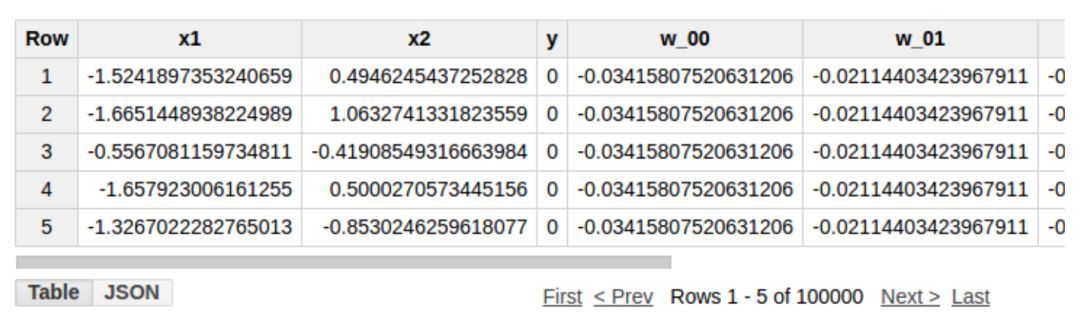
我們將使用 Bigquery 的函式 save to table 把結果儲存到一個新表。我們現在可以在訓練集上執行一次推理來比較預測值和預期值的差距。查詢陳述句片段在以下連結中:
https://github.com/harisankarh/nn-sql-bq/blob/master/query_for_prediction.sql。
僅透過十個迭代,我們的準確率就可達 93%(測試集上也差不多)。

如果我們把迭代次數加到 100 次,準確率高達 99%。
最佳化
下麵是對本專案的總結。我們由此獲得了哪些啟發?如你所見,資源瓶頸決定了資料集的大小以及迭代執行的次數。除了祈求谷歌開放資源上限,我們還有如下最佳化手段來解決這個問題。
-
建立中間表和多個 SQL 陳述句有助於增加迭代數。例如,前 10 次迭代的結果可以儲存在一個中間表中。同一查詢陳述句在執行下 10 次迭代時可以基於這個中間表。如此,我們就執行了 20 個迭代。這個方法可以反覆使用,以應對更大的查詢迭代。
-
相比於在每一步增加外查詢,我們應該盡可能的使用函式的巢狀。例如,在一個子查詢中,我們可以同時計算 scores 和 probs,而不應使用 2 層巢狀查詢。
-
在上例中,所有的中間項都被保留直到最後一個外查詢執行。其中有些項如
correct_logprobs可以早些刪除(儘管 SQL 引擎可能會自動的執行這類最佳化)。 -
多嘗試應用使用者自定義的函式。如果感興趣,你可以看看這個 BigQuery 的使用者自定義函式的服務模型的專案(但是,無法使用 SQL 或者 UDFs 進行訓練)。
意義
現在,讓我們來看看基於深度學習的分散式 SQL 引擎的深層含義。 BigQuery、Presto 這類 SQL 倉庫引擎的一個侷限性在於,查詢操作是在 CPU 而不是 GPU 上執行的。研究 blazingdb 和 mapd 等基於 GPU 加速的資料庫查詢結果想必十分有趣。一個簡單的研究方法就是使用分散式 SQL 引擎執行查詢和資料分佈,並用 GPU 加速資料庫執行本地計算。
退一步來看,我們已經知道執行分散式深度學習很難。分散式 SQL 引擎在數十年內已經有了大量的研究工作,並產出如今的查詢規劃、資料分割槽、操作歸置、檢查點設定、多查詢排程等技術。其中有些可以與分散式深度學習相結合。如果你對這些感興趣,請看看這篇論文(https://sigmodrecord.org/publications/sigmodRecord/1606/pdfs/04_vision_Wang.pdf),該論文對分散式資料庫和分散式深度學習展開了廣泛的研究討論。
希望你如我一般享受其中!請在下方分享你的高見。
●編號417,輸入編號直達本文
●輸入m獲取文章目錄

人工智慧與大資料技術
更多推薦《18個技術類公眾微信》
涵蓋:程式人生、演演算法與資料結構、駭客技術與網路安全、大資料技術、前端開發、Java、Python、Web開發、安卓開發、iOS開發、C/C++、.NET、Linux、資料庫、運維等。
 知識星球
知識星球