作為一名資料科學家，我們至少需要掌握哪些數學知識？本文為您一一列舉，並解讀它們。

1函式、變數、方程和圖表

1.1

必備的知識點

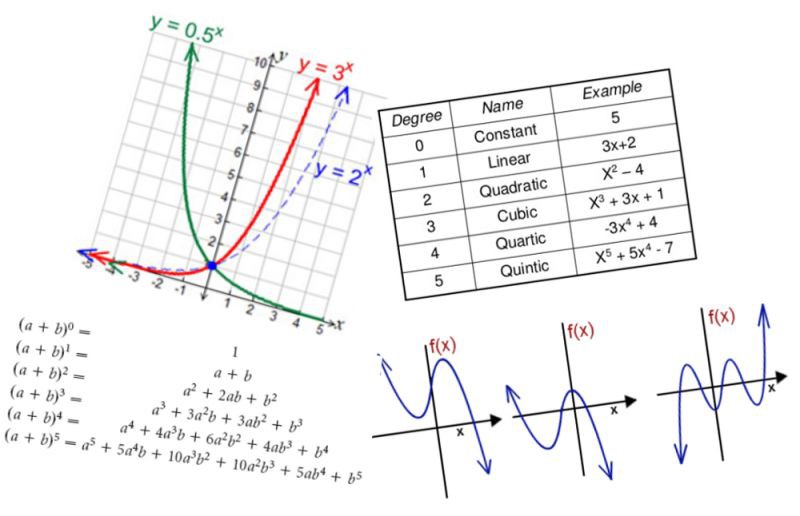
建議從最基本的知識點（如線性方程組、二項式定理）開始入手，重點掌握：

對數，指數，多項式函式，有理數。
基本幾何定理，三角恆等式。
實數和複數的基本屬性。
序列，加總，不等式。
繪圖，笛卡爾系、極坐標系，圓錐曲線。

1.2

常用知識點的舉例

如果您想要在排序後瞭解搜尋在百萬級別資料庫上的執行速度，您將會遇到二進位制搜尋的概念。要瞭解它的動態變化，需要瞭解對數和遞推方程。或者，如果您想分析時間序列，您可能會遇到週期函式和指數衰減等概念。

1.3

學習資源的推薦

Data Science Math Skills — Coursera
Introduction to Algebra — edX
Khan Academy Algebra

2 統計學

2.1

必備知識點

在資料科學家成長的過程中，不能過度強調掌握統計和機率的重要性。很多人甚至認為經典的機器學習（非神經網路）只是統計學習。這個主題太過於廣泛了。因此，畫清楚重點是很有必要的。

資料摘要和描述性統計，集中趨勢，方差，協方差，相關性，
機率的基本概念，期望，機率演算，貝葉斯定理，條件機率，
機率分佈函式：均勻分佈，正態分佈，二項式分佈，卡方分佈，學生t-分佈，中心極限定理，
取樣，測量，誤差，隨機數生成，
假設檢驗，A / B檢驗，置信區間，p值，
方差分析，t檢驗
線性回歸，正則化

2.2

常用知識點的舉例

在同行交流中，如果你能掌握以上所有的概念，你會很快給對方留下深刻的印象。作為資料科學家，你幾乎處處都要用到這些概念。

2.3

學習資源的推薦

Statistics with R specialization — Coursera, Duke University
Statistics and Probability in Data Science using Python — edX, Univ of California San Diego
Business Statistics and Analysis Specialization — Coursera, Rice University

3 線性代數

3.1

必備知識點

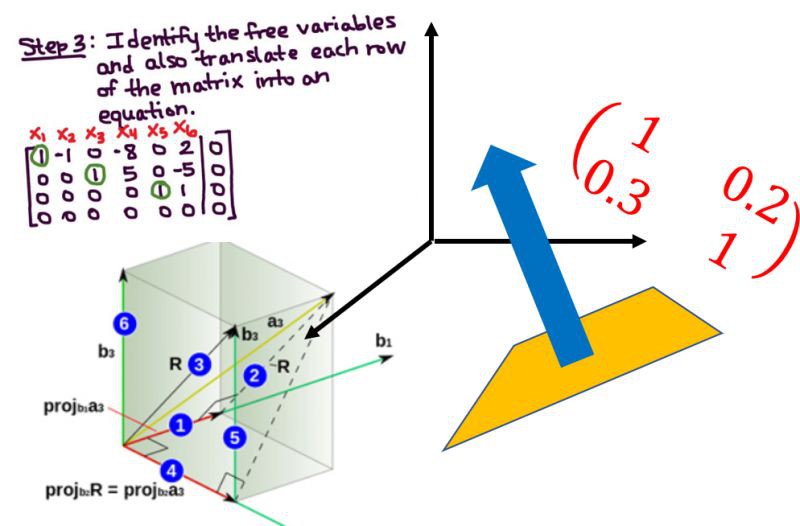
什麼是常用的？矩陣和矩陣代數。這是學習數學的一個重要分支，用於理解大多數機器學習演演算法如何在資料流上工作以建立洞察力。以下是要學習的基本內容

可矩陣和向量的基本屬性 – 標量乘法，線性變換，轉置，共軛，秩，行列式，
矩陣乘法規則和各種演演算法，矩陣逆，
特殊矩陣 – 方陣，單位矩陣，三角矩陣，稀疏和密集矩陣的思想，單位向量，對稱矩陣，Hermitian，skew-Hermitian和酉矩陣，
矩陣分解概念/ LU分解，高斯/高斯 – 喬丹消除，求解Ax = b方程的線性系統，
向量空間，基，跨度，正交性，線性最小二乘，
特徵值，特徵向量和對角化，奇異值分解（SVD）

3.2

常用知識點的舉例

如果您使用了降維技術主成分分析（PCA），那麼您可能已經使用奇異值分解來實現資料降維。通常，絕大多數神經網路演演算法都使用線性代數技術來表示和處理網路結構和學習操作。

3.3

學習資源的推薦

Linear Algebra: Foundation to Frontier — edX, UT Austin
Mathematics for Machine Learning: Linear Algebra — Coursera, Imperial College, London

4 微積分

4.1

必備的知識點

無論你喜歡它還是在大學期間都討厭它，事實上微積分的概念和應用在資料科學或機器學習領域的許多地方出現。它隱藏線上性回歸中普通最小二乘問題的簡單分析解決方案背後，或者嵌入到神經網路學習新樣式的每個反向傳播中。以下是要學習的方面。

單變數，極限，連續性和可微性
中值定理，不確定形式和L’Hospital規則，
極小值，
泰勒序列，無限級數求和/積分概念
積分計算的基本和中值定理，對有限和不正確積分的評價，
Beta和Gamma功能，
多變數的函式，極限，連續性，偏導數，
普通和偏微分方程的基礎知識

4.2

常用知識點的舉例

想知道如何實現邏輯回歸演演算法？它很有可能使用一種稱為“梯度下降”的方法來找到最小損失函式。要瞭解這是如何實現的，您需要使用來自微積分的概念 – 梯度，導數，極限和鏈式求導法則。

4.3

學習資源的推薦

Pre-University Calculus — edX, TU Delft
Khan Academy Calculus all content
Mathematics for Machine Learning: Multivariable Calculus — Coursera, Imperial College, London

5 離散數學

5.1

必備的知識點

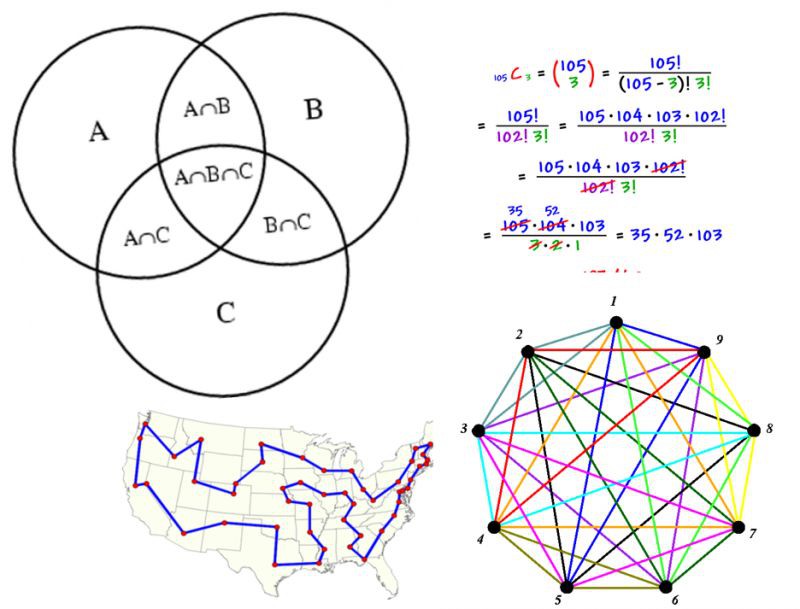
通常，離散數學是“資料科學的數學”中較少討論的主題，但事實是所有現代資料科學都是在計算系統的幫助下完成的，離散數學是這類系統的核心。這裡是要學習的一些重點。

集，子集，冪集
計數功能，組合，可數性
基本證明方法 – 歸納法、反證法
歸納，演繹和命題邏輯的基礎知識
基本資料結構 – 堆疊，佇列，圖形，陣列，雜湊表，樹
圖表屬性 – 連線元件，度，最大流量/最小切割概念，圖形著色
遞迴關係和方程
函式的增長和O（n）符號概念

5.2

常用知識點的舉例

在社交網路分析中，您需要知道圖的屬性和快速演演算法以搜尋和遍歷網路。在任何演演算法選擇中，您都需要透過使用 O（n）（Big-Oh）表示法來瞭解時間和空間複雜度，即執行時間和空間要求如何隨輸入資料大小而增長。

5.3

學習資源的推薦

Introduction to Discrete Mathematics for Computer Science Specialization — Cousera, Univ. of California San Diego
Introduction to Mathematical Thinking — Coursera, Stanford
Master Discrete Mathematics: Sets, Math Logic, and More — Udemy

6 最佳化論與運籌學

6.1

必備的知識點

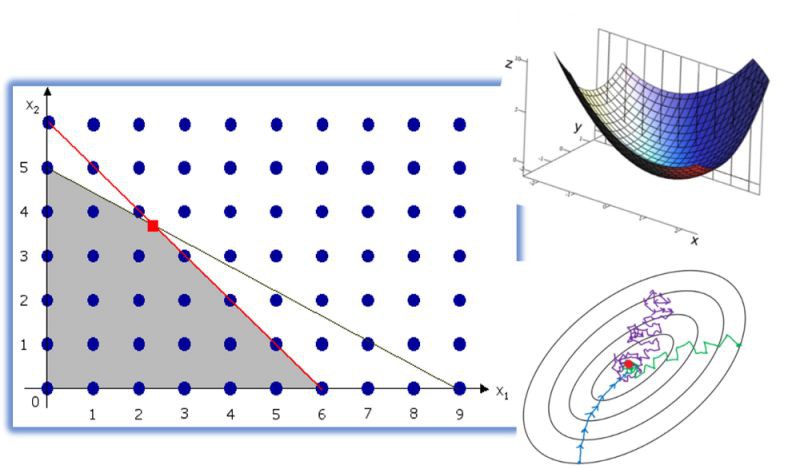
此部分與應用數學中的傳統話語沒什麼不同，因為它們在專業領域 – 理論電腦科學，控制理論或運籌學 – 中最為相關和最廣泛使用。然而，在機器學習的實踐中，對這些強大技術的基本理解可以非常有成效。實際上，每種機器學習演演算法/技術都旨在最小化受各種約束影響的某種估計誤差。那就是最佳化問題。要學習的內容：

最佳化的基礎 – 如何制定問題
最大值，最小值，凸函式，全域性解
線性規劃，單純形演演算法
整數程式設計
約束程式設計，揹包問題

6.2

常用知識點的舉例

使用最小平方損失函式的簡單線性回歸問題通常具有精確的解析解。但邏輯回歸問題卻沒有。要理解原因，您需要瞭解最佳化中凸性的概念。這一調查也將闡明為什麼我們必須對大多數機器學習問題中的“近似”解決方案保持滿意。

6.3

學習資源的推薦

Optimization Methods in Business Analytics — edX, MIT
Discrete Optimization — Coursera, University of Melbourne
Deterministic Optimization — edX, Georgia Tech

備註，本文由李昊璟、朝樂門負責翻譯、編輯、排版和校對。原文提名為《Essential Math for Data Science — ‘Why’ and ‘How》，作者為Tirthajyoti Sarkar，URL為https://towardsdatascience.com/essential-math-for-data-science-why-and-how-e88271367fbd。轉載請註明出處。

版權宣告：本號內容部分來自網際網路，轉載請註明原文連結和作者，如有侵權或出處有誤請和我們聯絡。