
筆者邀請您,先思考:
1 協同過濾演演算法的原理?
2 協同過濾演演算法如何預測?
什麼是協同過濾
協同過濾推薦(Collaborative Filtering recommendation)是在資訊過濾和資訊系統中正迅速成為一項很受歡迎的技術。與傳統的基於內容過濾直接分析內容進行推薦不同,協同過濾分析使用者興趣,在使用者群中找到指定使用者的相似(興趣)使用者,綜合這些相似使用者對某一資訊的評價,形成系統對該指定使用者對此資訊的喜好程度預測。
協同過濾是迄今為止最成功的推薦系統技術,被應用在很多成功的推薦系統中。電子商務推薦系統可根據其他使用者的評論資訊,採用協同過濾技術給標的使用者推薦商品。
協同過濾演演算法主要分為基於啟髮式和基於模型式兩種。
其中,基於啟髮式的協同過濾演演算法,又可以分為基於使用者的協同過濾演演算法(User-Based)和基於專案的協同過濾演演算法(Item-Based)。
-
啟髮式協同過濾演演算法主要包含3個步驟:
1)收集使用者偏好資訊;
2)尋找相似的商品或者使用者;
3)產生推薦。
“巧婦難為無米之炊”,協同過濾的輸入資料集主要是使用者評論資料集或者行為資料集。這些資料集主要又分為顯性資料和隱性資料兩種型別。其中,顯性資料主要是使用者打分資料,譬如使用者對商品的打分,五分制的1分,2分等。
但是,顯性資料存在一定的問題,譬如使用者很少參與評論,從而造成顯性打分資料較為稀疏;使用者可能存在欺詐嫌疑或者僅給定了部分資訊;使用者一旦評分,就不會去更新使用者評分分值等。
而隱性資料主要是指使用者點選行為、購買行為和搜尋行為等,這些資料隱性地揭示了使用者對商品的喜好。
隱性資料也存在一定的問題,譬如如何識別使用者是為自己購買商品,還是作為禮物贈送給朋友等。
1.基於使用者的協同過濾
用相似統計的方法得到具有相似愛好或者興趣的相鄰使用者,所以稱之為以使用者為基礎(User-based)的協同過濾或基於鄰居的協同過濾(Neighbor-based Collaborative Filtering)。
1.1方法步驟:
1.收集使用者資訊
收集可以代表使用者興趣的資訊。一般的網站系統使用評分的方式或是給予評價,這種方式被稱為“主動評分”。另外一種是“被動評分”,是根據使用者的行為樣式由系統代替使用者完成評價,不需要使用者直接打分或輸入評價資料。電子商務網站在被動評分的資料獲取上有其優勢,使用者購買的商品記錄是相當有用的資料。
2.最近鄰搜尋(Nearest neighbor search, NNS)
以使用者為基礎(User-based)的協同過濾的出發點是與使用者興趣愛好相同的另一組使用者,就是計算兩個使用者的相似度。例如:查詢n個和A有相似興趣使用者,把他們對M的評分作為A對M的評分預測。一般會根據資料的不同選擇不同的演演算法,目前較多使用的相似度演演算法有Pearson Correlation Coefficient(皮爾遜相關係數)、Cosine-based Similarity(餘弦相似度)、Adjusted Cosine Similarity(調整後的餘弦相似度)。
基於使用者(User-Based)的協同過濾演演算法首先要根據使用者歷史行為資訊,尋找與新使用者相似的其他使用者;同時,根據這些相似使用者對其他項的評價資訊預測當前新使用者可能喜歡的項。
給定使用者評分資料矩陣R,基於使用者的協同過濾演演算法需要定義相似度函式s:U×U→R,以計算使用者之間的相似度,然後根據評分資料和相似矩陣計算推薦結果。
1.2如何選擇合適的相似度計算方法
在協同過濾中,一個重要的環節就是如何選擇合適的相似度計算方法,常用的兩種相似度計算方法包括皮爾遜相關係數和餘弦相似度等。皮爾遜相關係數的計算公式如下所示:

皮爾遜相關係數
其中,i表示項,例如商品;Iu表示使用者u評價的項集;Iv表示使用者v評價的項集;ru,i表示使用者u對項i的評分;rv,i表示使用者v對項i的評分;表示使用者u的平均評分;表示使用者v的平均評分。
另外,餘弦相似度的計算公式如下所示:

餘弦相似度
1.3計算使用者u對未評分商品的預測分值
另一個重要的環節就是計算使用者u對未評分商品的預測分值。首先根據上一步中的相似度計算,尋找使用者u的鄰居集N∈U,其中N表示鄰居集,U表示使用者集。然後,結合用戶評分資料集,預測使用者u對項i的評分,計算公式如下所示:

預測使用者u對項i的評分
其中,s(u,u’)表示使用者u和使用者u’的相似度。
1.4透過例子理解
假設有如下電子商務評分資料集,預測使用者C對商品4的評分。

電子商務評分資料集
表中?表示評分未知。根據基於使用者的協同過濾演演算法步驟,計算使用者C對商品4的評分,其步驟如下所示。
(1)尋找使用者C的鄰居
從資料集中可以發現,只有使用者A和使用者D對商品4評過分,因此候選鄰居只有2個,分別為使用者A和使用者D。使用者A的平均評分為4,使用者C的平均評分為3.667,使用者D的平均評分為3。

image.png
根據皮爾遜相關係數公式:
紅色區域計算C使用者與A使用者,使用者C和使用者A的相似度為:
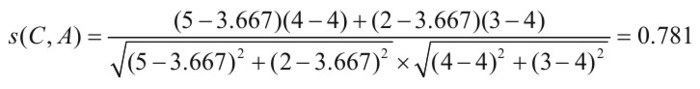
使用者C和使用者A的相似度
藍色區域計算C使用者與D 使用者的相似度為:

C使用者與D 使用者的相似度
(2)預測使用者C對商品4的評分
根據上述評分預測公式,計算使用者C對商品4的評分,如下所示:

使用者C對商品4的評分
依此類推,可以計算出其他未知的評分。
2.基於專案的協同過濾
以使用者為基礎的協同推薦演演算法隨著使用者數量的增多,計算的時間就會變長,所以在2001年Sarwar提出了基於專案的協同過濾推薦演演算法(Item-based Collaborative Filtering Algorithms)。以專案為基礎的協同過濾方法有一個基本的假設“能夠引起使用者興趣的專案,必定與其之前評分高的專案相似”,透過計算專案之間的相似性來代替使用者之間的相似性。
2.1方法步驟:
1.收集使用者資訊
同以使用者為基礎(User-based)的協同過濾。
2.針對專案的最近鄰搜尋
先計算已評價專案和待預測專案的相似度,並以相似度作為權重,加權各已評價專案的分數,得到待預測專案的預測值。例如:要對專案 A 和專案 B 進行相似性計算,要先找出同時對 A 和 B 打過分的組合,對這些組合進行相似度計算,常用的演演算法同以使用者為基礎(User-based)的協同過濾。
3.產生推薦結果
以專案為基礎的協同過濾不用考慮使用者間的差別,所以精度比較差。但是卻不需要使用者的歷史資料,或是進行使用者識別。對於專案來講,它們之間的相似性要穩定很多,因此可以離線完成工作量最大的相似性計算步驟,從而降低了線上計算量,提高推薦效率,尤其是在使用者多於專案的情形下尤為顯著。
基於專案(Item-Based)的協同過濾演演算法是常見的另一種演演算法。與User-Based協同過濾演演算法不一樣的是,Item-Based協同過濾演演算法計算Item之間的相似度,從而預測使用者評分。也就是說該演演算法可以預先計算Item之間的相似度,這樣就可提高效能。Item-Based協同過濾演演算法是透過使用者評分資料和計算的Item相似度矩陣,從而對標的Item進行預測的。
2.2相似度計算方法
和User-Based協同過濾演演算法類似,需要先計算Item之間的相似度。並且,計算相似度的方法也可以採用皮爾遜關係繫數或者餘弦相似度,這裡給出一種電子商務系統常用的相似度計算方法,即基於物品的協同過濾演演算法,其中相似度計算公式如下所示:

image.png
這裡,分母|N(i)|是喜歡物品i的使用者數,而分子|N(i)∩N(j)|是同時喜歡物品i和j的使用者,但是如果物品j很熱門,就會導致Wij很大接近於1。因此避免推薦出熱門的物品,我們使用下麵的公式:

基於物品的相似度
從上面的定義可以看出,在協同過濾中兩個物品產生相似度是因為他們共同被很多使用者喜歡,也就是說每個使用者都可以透過他們的歷史興趣串列給物品“貢獻”相似度。
計算物品相似度首先建立使用者-物品倒排表(即對每個使用者建立一個包含他喜歡的物品的串列),然後對每個使用者,將他物品串列中的物品兩兩在共現矩陣中加1。

程式碼

圖例
根據矩陣計算每兩個物品之間的相似度wij。
2.3使用者u對於物品j的興趣
得到物品之間的相似度後,可以根據如下公式計算使用者u對於物品j的興趣:
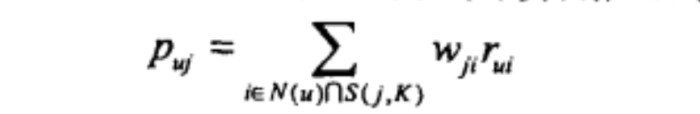
使用者u對於物品j的興趣
這裡N(u)是使用者喜歡的物品的集合,S(j,K)是和物品j最相似的K個物品的集合,wji是物品j和i的相似度,rui是使用者u對物品i的興趣。(對於隱反饋資料集,如果使用者u對物品i有過行為,即可令rui=1。)該公式的含義是,和使用者歷史上感興趣的物品越相似的物品,越有可能在使用者的推薦串列中獲得比較高的排名。
當我們看到這裡的時候很可能由於自己功底不足,很難看懂公式中的i∈N(u)∩S(j,K)。
我們來看另外一種計算方式:

矩陣
其中,Pa為新使用者對已有產品的向量,T為物品的共現矩陣,得到的P`a為新使用者對每個產品的興趣度。
那麼就可以理解上述公式的i∈N(u)∩S(j,K),我們在下麵的例子中詳細講解。
2.4舉例
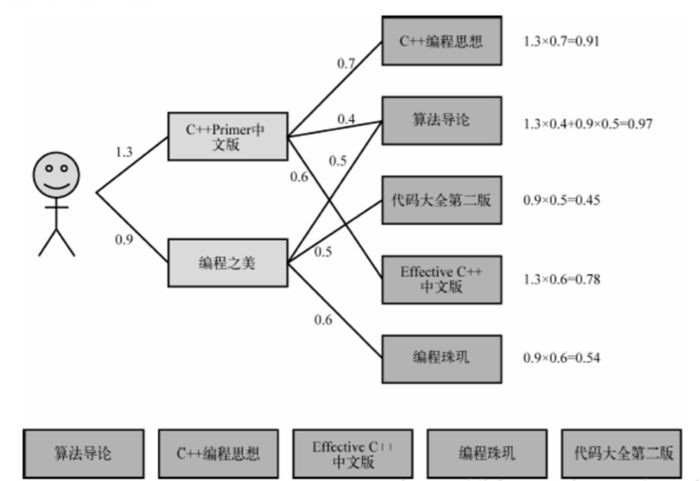
現有使用者的訪問的記錄如下圖所示:

使用者的訪問
他的共現矩陣為:

共現矩陣
透過公式計算相似度:

Wa,b
以此類推得到相似度的共現矩陣:

相似度的共現矩陣
此時若有新使用者E,訪問的a,b,d三個物品,那麼可以看做向量P:

向量P
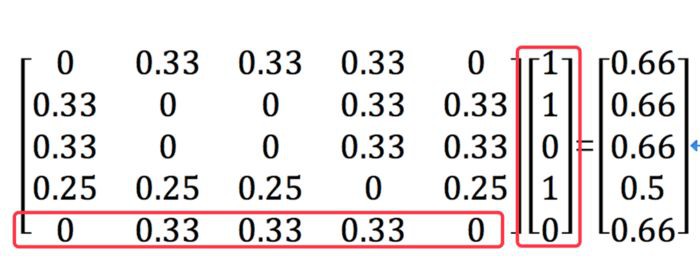
那麼P`為矩陣相乘:

P`
此時得到了對於使用者E,c和e兩個物品的興趣度是相同的。
2.5理解公式i∈N(u)∩S(j,K)
那麼現在我們來理解公式i∈N(u)∩S(j,K):
對於使用者E,已經訪問了a,b,d,那麼,N(u)={a,b,d};還有兩個未訪問物品c,e,那麼j={c,e};
當j=c時,對於和物品j最相似的K個物品的集合為{a,d,e},那麼S(j,K)={a,d,e};得出N(u)∩S(j,K)={a,d},如下圖所示:

再來看矩陣相乘中的c行,乘以P,實際上就是上述N(u)∩S(j,K)={a,d}的相似度求和。

同理,當j=e時,對於和物品j最相似的K個物品的集合為{b,c,d},那麼S(j,K)={b,c,d};得出N(u)∩S(j,K)={b,d};如下圖所示:
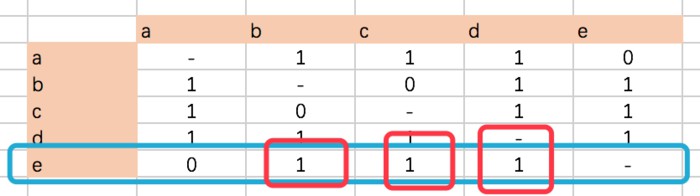
再來看矩陣相乘中的e行,乘以P,實際上就是上述N(u)∩S(j,K)={b,d}的相似度求和。
連結:
https://www.jianshu.com/p/5463ab162a58
您有什麼見解,請留言。
文章推薦:
加入資料人圈子或者商務合作,請新增筆者微信。

資料人網是資料人學習、交流和分享的平臺http://shujuren.org 。專註於從資料中學習到有用知識。
平臺的理念:人人投稿,知識共享;人人分析,洞見驅動;智慧聚合,普惠人人。
您在資料人網平臺,可以1)學習資料知識;2)建立資料部落格;3)認識資料朋友;4)尋找資料工作;5)找到其它與資料相關的乾貨。
我們努力堅持做原創,聚合和分享優質的省時的資料知識!
我們都是資料人,資料是有價值的,堅定不移地實現從資料到商業價值的轉換!
點選閱讀原文,進入資料人網,獲取資料知識。
公眾號推薦:
鏈達君,專註於分享區塊鏈內容。

腳印英語,專註於分享英語口語內容。

 知識星球
知識星球