小編邀請您,先思考:
1 為什麼KNN演演算法在增大k時,偏差會變大?
2 RF增大樹的數目時偏差卻保持不變,GBDT在增大樹的數目時偏差卻又能變小?
在機器學習的面試中,能不能講清楚偏差方差,經常被用來考察面試者的理論基礎。偏差方差看似很簡單,但真要徹底地說明白,卻有一定難度。比如,為什麼KNN演演算法在增大k時,偏差會變大,但RF增大樹的數目時偏差卻保持不變,GBDT在增大樹的數目時偏差卻又能變小。本文的目的就是希望能對偏差方差有一個科學的解讀,歡迎大家多多交流。
01
引子
假設我們有一個回歸問題,我們搞到一批訓練資料D,然後選擇了一個模型M,並用資料D將M訓練出來,記作Mt,這裡我們故意把模型M與訓練出的模型Mt區分開,是為了後面敘述時概念上的清晰。現在,我們怎麼評價這個模型的好壞呢?
你可能會不屑地說,這麼簡單的問題還用問嗎,當然是用test集來測試啊。
哈哈!你上當了!
因為我並沒有說明是評價模型M的好壞還是模型Mt的好壞!這二者有什麼區別呢?
我們都知道,模型M代表的是一個函式空間,比如模型y=wx+b,若x,y都是實數,w,b為實數引數,則該模型就代表了平面上所有的直線,這所有的直線就是一個函式空間。
同理,y=ax^2+bx+c代表的就是平面上所有的二次曲線,所有的二次曲線組成一個函式空間。當然,所有的直線此時也是二次曲線的特例。
回到上面的問題,Mt實際上是用資料D找到的M代表的函式空間中的一個具體的函式。這話有點繞,不過還是不難理解的。
Mt的表現好壞不能完整地代表M的好壞。
上面這句話有很多內涵,我們一點一點來說明。
02
什麼是M的好壞
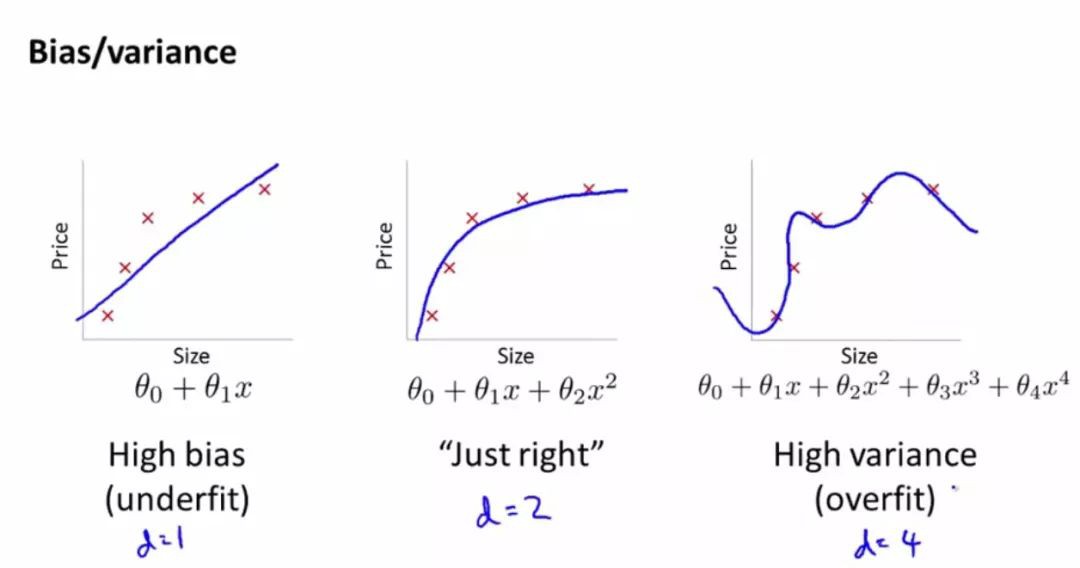
以上面的一次函式和二次函式為例,當我們說二次函式比一次函式更好時,我們潛在的含義是說,對於某個我們正要解決的機器學習問題來說,二次函式總體上比一次函式表現更好,我們是在函式空間的層次上來比較的。
而且,還是針對一個具體的機器學習問題來比較的,因為對於不同的機器學習問題,二者哪個更好是不一定的。
Note:在下文中,可以把機器學習問題默想成回歸問題,這樣便於理解。
這裡再次強調,當我們說模型好壞時,隱含有兩個含義:
1)比較的是整個函式空間
2)針對某個具體機器學習問題比較
03
怎麼比較M的好壞?
我們可以這樣做:
1)找一條不變的萬能測試樣本
在這個具體的機器學習問題中找一條樣本x,它的標簽為y。在後續的所有訓練中都用這條樣本做測試集,永遠不用作訓練集。
2)在測試樣本上觀察Mt的表現,假設Mt在樣本x上的預測值為yt,則y-yt可用來評價Mt的表現好壞。
3)找另外一個訓練集D1,訓練出Mt1,在測試樣本上測試得到yt1,進而得到誤差y-yt1,
4)重覆第3步多次,直到得到N個具體的模型,和N個yt,N個y-yt。
5)當N足夠大時,我們可以這樣來評測M的好壞,首先看N個yt的均值ytmean是否等於y,其次,看N個yt相對均值ytmean的方差有多大。
顯然,若ytmean=y,說明M學習能力是夠的,也就是說,當N趨向無窮大時,N個Mt對x預測的均值能無限接近y。
很多人會有種錯覺,感覺任何M都能達到上面的效果,實際上,不是每一個M都有這樣的能力的,舉個極端的例子,我們假設M1的函式空間中只有一個函式,且對於任何樣本的預測值都恆等於y+1,則無論N多大,ytmean都會比y大1的。我們稱M1由於學習能力不夠所造成的對x的預測誤差叫做偏差。
其次,N個yt相對均值ytmean的方差有多大也能從另一個方面揭示M的好壞,舉個例子,假設我們有M1,M2兩個模型,當N無窮大時,都能使得ytmean等於y。但是M1的預測值是這樣分佈的(下麵圓點代表一個個的預測值)
…..ytmean…..
M2的預測值是這樣分佈的
. . . .ytmean. . . .
顯然,我們會覺得M1比M2更好。你可能會想,N足夠大時,二者都能準確地均值到y,這就夠了,沒必要再比較它們的預測值相對均值的方差。
這樣的觀點錯誤的地方是:實踐中,我們並不能抽樣出D1,D2,D3…….DN個訓練集,往往只有一份訓練集D,這種情況下,顯然,用M1比用M2更有把握得到更小的誤差。
04
舉例子來說明偏差方差
假設模型是一個射擊學習者,D1,D2直到DN就是N個獨立的訓練計劃。
如果一個學習者是正常人,一個眼睛斜視,則可以想見,斜視者無論參加多少訓練計劃,都不會打中靶心,問題不在訓練計劃夠不夠好,而在他的先天缺陷。這就是模型偏差產生的原因,學習能力不夠。正常人參加N個訓練計劃後,雖然也不能保證打中靶心,但隨著N的增大,會越來越接近靶心。
假設還有一個超級學習者,他的學習能力特別強,參加訓練計劃D1時,他不僅學會了瞄準靶心,還敏感地捕捉到了訓練時的風速,光線,並據此調整了瞄準的方向,此時,他的訓練成績會很好。
但是,當參加測試時的光線,風速肯定與他訓練時是不一樣的,他仍然按照訓練時學來的瞄準方法去打靶,肯定是打不好。這樣產生的誤差就是方差。這叫做聰明反被聰明誤。
總結一下:學習能力不行造成的誤差是偏差,學習能力太強造成的誤差是方差。
05
權衡偏差方差
當我們只有一份訓練資料D時,我們選的M若太強,好比射手考慮太多風速,光線等因素,學出來的模型Mt在測試樣本上表現肯定不好,若選擇的M太挫,比如是斜視,也無論如何在測試的樣本上表現也不會好。所以,最好的M就是學習能力剛剛好的射手,它能夠剛剛好學習到瞄準的基本辦法,又不會畫蛇添足地學習太多細枝末節的東西。
06
回答本文最初的問題
對於KNN演演算法,k值越大,表示模型的學習能力越弱,因為k越大,它越傾向於從“面”上考慮做出判斷,而不是具體地考慮一個樣本 近身的情況來做出判斷,所以,它的偏差會越來越大。
對於RF,我們實際上是部分實現了多次訓練取均值的效果,每次訓練得到的樹都是一個很強的學習者,每一個的方差都比較大,但綜合起來就會比較小。好比一個很強的學習者學習時,颳著西風,它會據此調整自己的瞄準方法,另一個很強的學習者學習時颳著東風,(西風、東風可以理解為不同訓練集中的噪聲)它也會據此調整自己的瞄準方法,在測試樣本時,一個誤差向西,一個誤差向東,剛好起到互相抵消的作用,所以方差會比較小。但是由於每棵樹的偏差都差不多,所以,我們取平均時,偏差不會怎麼變化。
為什麼說是部分實現了多次訓練取均值的效果而不是全部呢?因為我們在訓練各棵樹時,是透過抽樣樣本集來實現多次訓練的,不同的訓練集中不可避免地會有重合的情況,此時,就不能認為是獨立的多次訓練了,各個訓練得到的樹之間的方差會產生一定的相關性,訓練集中重合的樣本越多,則兩棵樹之間的方差的相關性越強,就越難達成方差互相抵消的效果。
對於GBDT,N棵樹之間根本就不是一種多次訓練取均值的關係,而是N棵樹組成了相關關聯,層層遞進的超級學習者,可想而知,它的方差一定是比較大的。但由於它的學習能力比較強,所以,它的偏差是很小的,而且樹的棵樹越多,學習能力就越強,偏差就越小。也就是說,只要學習次數夠多,預測的均值會無限接近於標的。簡單講就是GBDT的N棵樹實際上是一個有機關聯的模型,不能認為是N個模型。
原文連結:https://www.jianshu.com/p/23550b50b6c1
親愛的讀者朋友們,您們有什麼想法,請點選【寫留言】按鈕,寫下您的留言。
資料人網(http://shujuren.org)誠邀各位資料人來平臺分享和傳播優質資料知識。
公眾號推薦:
360區塊鏈,專註於360度分享區塊鏈內容。

閱讀原文,更多精彩!
分享是收穫,傳播是價值!
 知識星球
知識星球