作者丨王維塤
學校丨天津大學碩士生
研究方向丨DRL & MAS
以彼之道還施彼身

■ 論文 | Maintaining Cooperation in Complex Social Dilemmas Using Deep Reinforcement Learning
■ 連結 | https://www.paperweekly.site/papers/1558
為什麼要叫做以彼之道還施彼身,是因為這篇文章借鑒了 TFT 的思想,擴充套件成 amTFT。而我對 TFT 的第一反應就是姑蘇慕容的以彼之道還施彼身。
這篇文章是 Facebook AI Research 投在今年 ICLR 上面的文章。不算很好,但是想要解決的問題還是很有意義的,所以大家可以辨證地看這篇文章,希望能讓各位有所收穫。
核心問題
1. 研究問題:在 complex social dilemmas 中如何設計出既能考慮 social welfare,又能確保自己 payoff 的 agent。
2. 假設條件:能夠觀察到對手的 action,能夠事先知道環境。
3. 主要想法:如果想要最大化 social welfare,那麼就是在對手能夠合作的時候與對手合作。要確保自己的 payoff,就是在對手背叛的時候,自己也背叛,確保自己不會被對手利用。
4. 解決方案:
-
事先訓練出 fully cooperative policy 與 safe policy(defection)的策略,同時獲得雙方都合作/競爭時的 Q 與 V;
-
然後透過對比對手當前 action 的 Q(合作)的值與對手當前 action 的 Q(合作)的值,如果當前 action 的 Q 值更高,就說明對手採用背叛的action;
-
累積對手背叛的程度,在一定閾值後,採用 K 次背叛的策略(K 的次數類似懲罰,採用 V 值進行計算),然後再切換成合作的策略,再次迴圈。
Background
關於 social dilemma,簡單地說就是 agent 們相互合作能夠得到比較高的 payoff,同時 total payoff 是最高的,但是不論在什麼情況下,採用 selfish 的 action 能夠比採用合作的 action 獲得更高的 payoff,所以 agent 為了自己的 payoff 有動機採用 selfish 的 action。
但是雙方都採用 selfish 的 action 時,payoff 反而比都合作時候的 payoff 低,同時 total payoff 也比較低。
通常對於 social dilemma 的研究環境,我們都採用是 repeat game,就是固定一個矩陣的 game,然後不停地玩這個 game。
在 Deepmind 的 Multi-agent Reinforcement Learning in Sequential Social Dilemmas 中,將 social dilemma 擴充套件到了 sequential 下,因為環境更複雜了也帶來更多的挑戰。
比如 defection 和 cooperative 是體現在一些列 actions 中,我們很難透過 actions 來判斷是合作還是競爭,同時傳統的 ISD 直接的方法不能直接擴充套件到 SSD 下麵。
那麼我們自然會想到使用 DRL。在複雜的 mas 環境中,我們通常使用 DRL+self-play 來訓練 agent,用簡單地話說,self-play 就是不斷重覆模擬 game,在模擬中控制所有的 agent,並不斷地 improving 這些 agent 的策略,並最終獲得訓練好的策略,在面對新的,未知的對手時,採用訓練好的 policy 來應對。
本文思路
但是在 SSD 中,我們並不能簡單地使用 DRL+self-play 來訓練 agent,主要原因是一個一直採用 cooperative policy 的 agent 容易被對手利用,一個一直採用 defection policy 的 agent 最終只能與一個理智的對手達成 social dilemma。
因此我們應該設計出一種演演算法,讓 agent 能夠根據對手的行為來調整採用 cooperative 還是 defection。
一個經典的做法叫做 Tit For Tat(TFT),TFT 就是在第一局採用合作,然後在以後的局面中採用對手上一局採用的 action。
說來簡單,但是 TFT 是一個非常強大的演演算法,能夠與能合作的對手合作,避免被對手利用,同時一旦對手能夠選擇合作,就會選擇合作,並有希望一直保持合作。
從描述中,我們就能很直觀地發現 TFT 並不能直接用在 SSD 的情況下,主要的原因是環境已經從一個矩陣,變成一個需要做序列決策的環境了。
雖然 TFT 不能直接用,但是我們可以利用 TFT 的思想來構造一個與 DRL 相互結合的演演算法,也就是這裡的演演算法:APPROXIMATE MARKOV TFT(amTFT)。
TFT 能夠直接用上一局對手的 action 來選擇自己這句的 action 的主要原因就是,在傳統的矩陣形式的 game 中,action,reward,defection,cooperative 這幾個其實可以理解為等價的,一者確定之後,其他就確定了。
比如我選擇 defection 的 action,那麼它的 reward 資訊就大致確定了(因為還與對手的 action 相關),所以在這裡我不嚴謹地說:選擇 action,本質上也就是在利用 reward 的資訊。
那麼就很直觀,在矩陣下麵我利用 reward 的資訊,在一個序列的決策中,我們就可以利用 Q 或者 V 的資訊,amTFT 就是利用 Q 與 V 的資訊。
具體做法
首先,我們採用 selfish 的方式,每個 agent 都是最大化自己的 reward 的方式,來訓練自己的 policy,我們可以得到 agent ![]() 的策略 , 相應的 Q function approximations
的策略 , 相應的 Q function approximations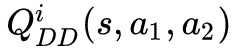 。
。
然後我們在採用 fully cooperation 的方式,agent 標的是最大化 total payoff 的方式來訓練策略,同樣我們可以得到 agent 的策略![]() , 相應的Q function approximations
, 相應的Q function approximations 。
。
那麼如果我們要衡量在當前 state s 下,我們合作時(假設我們是 agent1 ,對手是 agent2),對手當前 action 是否是合作的?
我們可以使用雙方都合作的時的 ,假設對手採用合作策略
,假設對手採用合作策略![]() 時,和當前採用 action 的 Q 的差值,如果當前 action 的 Q 值,則說明對手採用了競爭的 action,即為下式:
時,和當前採用 action 的 Q 的差值,如果當前 action 的 Q 值,則說明對手採用了競爭的 action,即為下式:

當 d 大於 0 時,我們覺得對手是採用競爭的策略,那麼我們可以變化自己的策略為競爭的策略。
在這裡 amTFT 的實際做法並不是像 TFT 那樣,不停地按照對手的 action 來調整自己的 action,而是變化為 defect 之後,保持 defect k step,然後調整為 cooperation,再次觀察對手的合作程度。
這裡就帶來兩個問題,一個問題是:一次 d 其實並不準確,容易有很大的誤差。另外的問題是:k step 的 k 該如何決定?
第一個問題其實比較好解決,我們可以不停的累積 d,直到 d 的累積和超過一個閾值,我們認為對手是 defect,然後再變換為 defect 的策略。這樣透過累積的方法,更加容忍 d 計算上可能的問題,但是實際上也帶來了一定的延遲性。
第二個問題其實也蠻重要的,因為如果採用固定的 k,容易被對手考慮全域性,在某個 s 下來利用這個性質。所以這裡採用類似懲罰的思想,使用第一個問題中累積的 d,來計算我應該懲罰對手多少局,它才會把這幾次背叛獲得更多的 payoff 損失掉:

其中 α 為超引數,大於 1,![]() 代表採用 D k step 後切換成 C。所以這裡其實是定義了一個下界。 整體的演演算法如下所示:
代表採用 D k step 後切換成 C。所以這裡其實是定義了一個下界。 整體的演演算法如下所示:

實驗

在這裡做了兩個實驗環境:
coin game:在一個 5×5 的格子世界中,有兩個不同顏色的 agent,也有兩個不同顏色的 coin,agent 不論收集到什麼顏色的 coin,agent 都會得到 +1 的 reward,但是如果 agent 收集到了另外顏色的 coin,對應顏色的 agent 會得到 -2 的 reward。
一般情況下,selfish 的 agent 就算不論什麼顏色都收集,合作的 agent 都只會收集自己的顏色的 coin。
Pong Player’s Dilemma (PPD):就是將 Pong 擴張成 SSD 的情況,贏球的 agent 獲得 +1 的 reward,輸球 的agent 獲得 -2 的 reward。所以 selfish 就是努力自己得分,合作就是雙方儘力不得分,在中間傳球。
在這兩個環境中,amTFT 達到了我們的目的:與合作的合作,與競爭的競爭,相互直接合作。

然後我們研究如果固定一個 agent 的策略,另外一個 agent 用 selfish 的角度,從頭開始學會怎麼樣(結果如上圖)。
這裡採用的固定的 agent 的策略為:合作,競爭,amTFT。面對合作/競爭的 agent 時,selfish 學到利用。面對 amTFT,selfish 最終學到合作。
小無相功

■ 論文 | RL^2: Fast Reinforcement Learning via Slow Reinforcement Learning
■ 連結 | https://www.paperweekly.site/papers/1560
小無相功可以模擬各種武功,只要你學了,各種武功皆數模仿,就向對 reinforcement learning 做 meta-learning,學會了 reinforcement learning,還有什麼學不會。
核心問題
1. 研究問題:如何對reinforcement learning進行learning,也就是meta-learning。
2. 假設條件:知道想要解決的問題的模型是什麼樣(能夠構造一大組(分佈)MDP)。
3. 主要想法:如果在一大組 MDP 中學習到的 agent,在面對未知(新的)MDP 時,能有不錯的效果,說明 agent 已經學到這類 MDP 的性質,也就是 prior。
4. 解決方案:用 RNN 來學習,用一大組 MDP 訓練出 RNN 的權重(視為 meta-learning),然後面對新的 MDP 時,用不斷產生的 input 來調整 hidden state,將不斷變化的 hidden state 是為當前 MDP 的 reinforcement learning。
思路
通常我們都是針對具體型別的問題設計相應的演演算法,因為是針對具體型別的設計,所以這樣的演演算法必然效能等方面會比較好,但是也因為是對於具體型別設計的,所以必然會有更多的侷限性,對於別的型別可能並不適用。
因此我們會想:能不能有萬能演演算法能夠針對不同型別的問題,學習出相應的型別,然後自己根據問題型別,來學習設計出演演算法?
deep learning 已經具有一定提取特徵的能力了,所以懶惰的我們肯定會想如果 agent 能夠根據問題自己調整齣網路結構那該多好。這有點跑題了,但這也就是這篇文章,或者 meta-learning 所希望有的能力:learning to learn。
不同型別的問題和不同型別的演演算法有不同的學習正規化。對於 Reinforcement Learning 當然最重要的一點是:MDP,因為 RL 的目的是針對特定的 MDP 學習出最優或者不錯的 policy。
那麼我們希望能夠讓 agent 學習到 RL 的能力,那其實就是希望能夠學習到在不同 MDP 中尋找最優 policy 或者不錯 policy 的能力。
這其實有點大,或者說有點難,因為 MDP 的各個部分其實有很多的伸縮性,所以對 training 等方面是有很大的挑戰的。
因此本文其實做了一個假設:我們事先知道要解決是什麼問題,根據這個問題的型別,構造了一堆 MDP,然後在這堆 MDP 中學出 MDP 中的特性,並將其應用在這個問題上,說明我的 agent 已經學習到了這類 MDP 的性質。
具體做法
PRELIMINARIES
discrete-time finite-horizon discounted Markov decision process (MDP) .

RL^2
如果我們使用 RNN 來構造 agent,agent 的輸入為:以前的 rewards,actions,termination flags 和 normal received observations。
同時 RNN 的 hidden state 並不在每次 episode 開始後重置,而是保留,然後使用標準的 RL 演演算法來 training 這個 agent,那麼這個 agent 應該能 capacity to perform learning in its own hidden activations。
這個 agent 在 deployed 時,面對未知的 MDP 應該能夠根據當前的資訊來調整 hidden state,也就是學習到了 RL 的能力,這也正是本文被稱之為 RL^2 的原因。

首先定義一個 MDPs 的知識,也就是在一大堆 MDP 中每個 MDP 被抽樣的機率: ,然後每次我們透過這個 M 來抽取MDP,抽取後將這個 MDP 固定 n 個 episode,比如上面的圖就是固定了 2 個 episode,也就是 n=2 。然後再繼續抽取新的 MDP,這樣不斷的學。
,然後每次我們透過這個 M 來抽取MDP,抽取後將這個 MDP 固定 n 個 episode,比如上面的圖就是固定了 2 個 episode,也就是 n=2 。然後再繼續抽取新的 MDP,這樣不斷的學。
這裡的細節是:agent 會使用上一時刻的 reward![]() ,上一時刻的action
,上一時刻的action![]() ,上一時刻的termination flag
,上一時刻的termination flag![]() (從上圖可知,我們時是固定了一個 MDP n episode,所以需要明顯地知道結束)和當前的state
(從上圖可知,我們時是固定了一個 MDP n episode,所以需要明顯地知道結束)和當前的state![]() 做為agent的輸入的。
做為agent的輸入的。
另一個重點是:我們是最大化這 n 個 episode 的 expected total discounted reward,這其實等價於 minimizing the cumulative pseudo-regret。
同時因為我們每次都是抽去出的 MDP,所以 agent 並不知道面對的是哪一個 MDP,所以 agent 應該要能夠利用歷史上的 input 推測出這個 MDP 的資訊,然後調整 policy,也就是 hidden state。
MULTI-ARMED BANDITS
就是經典的多臂賭博機,這裡存在很多個臂,然後從這些臂裡面抽取出一些臂做為一個賭博機來學習,每個臂被抽出的機率為 p_i ,所以是可以抽取多個賭博機,這就是上面說的 MDP 的 set,我們的目的是:maximize the total reward obtained over a fixed number of time steps。
這是個單狀態的問題,但是也要平衡探索與利用,因為研究的比較多,同時有 rich theory,可以與一些有理論保證,漸進線形最優的 policy 做對比,If the learning is successful, the resulting policy should be able to perform competitively with the theoretically optimal algorithms.
這裡與幾個 policy 做了對比:
-
random
-
gittins index
-
UCB1
-
Thompson sampling (TS)
-
ε-greedy
-
greedy
同時,我們把所有的 true distribution 提供給上面需要的演演算法( RL^2 除外)。

還是不錯的,但是因為已有的演演算法 mostly designed to minimize asymptotic regret (rather than finite horizon regret), hence there tends to be a little bit of room to outperform them in the finite horizon settings.
另外發現說在 n=500,k=50 和 index 有一些差距,為了探索是不是學出來的 RL 不夠好,就使用相同網路結構,然後用 index 來生成資料對網路做 SL,發現能學的和 index 差不多,說明 RL 學的還是有提升空間的。
TABULAR MDPS
多臂賭博機是一個單狀態的,但是 RL 是針對 sequential decision making 的,所以這裡就採用隨機生成 tabular MDP 來做測試。
這裡我們限制 state 空間為 10,action 空間為 5,rewards follow a Gaussian distribution with unit variance, and the mean parameters are sampled independently from Normal(1, 1) ,transitions are sampled from a flat Dirichlet distribution,然後 episode 的 horizon 為 T=10。
然後與下麵比較:
-
random
-
PSRL
-
BEB
-
UCRL2
-
ε-greedy
-
greedy
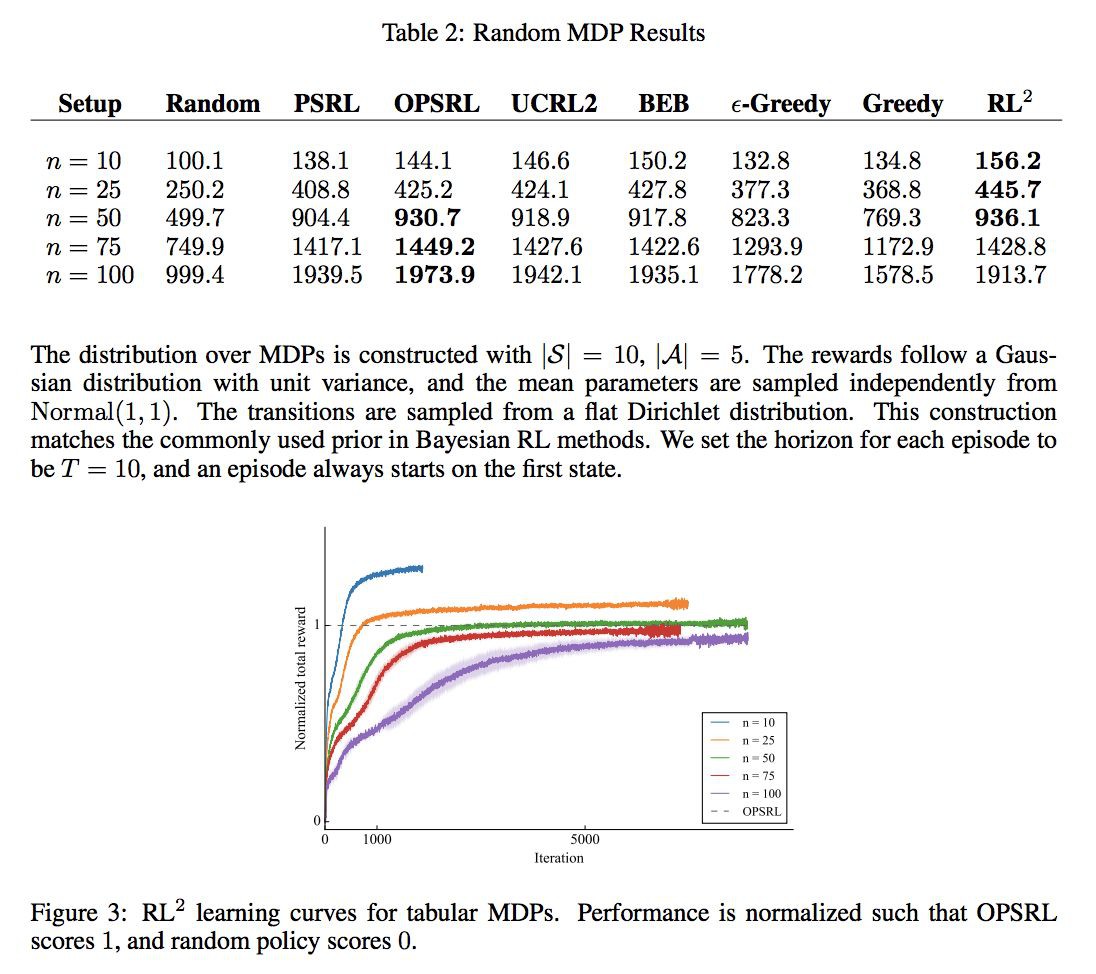
發現還是有一定效果的。
VISUAL NAVIGATION
每個 MDP 是隨機產生的 maze,然後標的是也是隨機的,但在一個 mdp 的不同 episode 下,maze 與終點時固定的。reward 和 cost 設定為:找到標的 reward+1,如果碰牆,cost 掉 -0.001,每個時間 step,cost 掉 -0.04。

先在 5×5 的世界中做 training,n=2,horizon=250。然後 maze 是從 1000 個 configuration 中產生的。在 test 時做了以下工作:1. 在 9×9 與 5×5 裡面看看效果如何;2. 將 agent 執行 5 個 episode 看看怎麼樣。
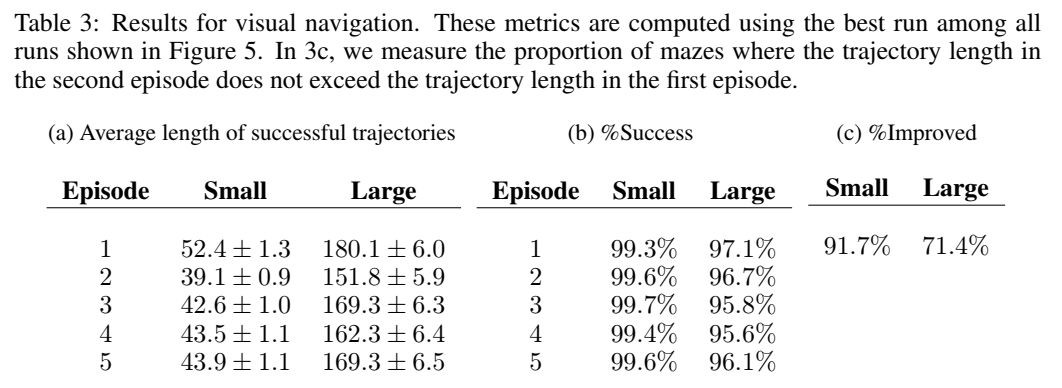
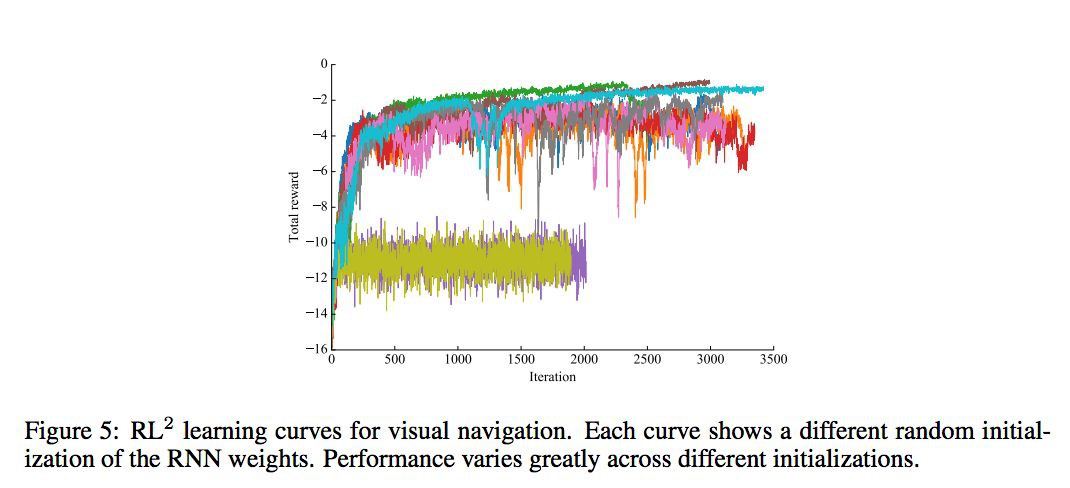
POLICY REPRESENTATION
輸入 (s, a, r, d) ,透過函式 Φ (s, a, r, d) 做 embedded 後做為 RNN 的輸入,RNN 的 cell 採用 GRU,然後在接一層全連線,再使用 softmax 做為啟用函式,輸入為每個 action 的機率。
另外這裡說引數在每個 episode 開始的時候重置一部分的 hidden state,這樣的目的其實是說開始和結束必然存在一些不一樣,希望學到這部分不一樣,但是實際實驗並沒有效果。
採用 off-the-shelf RL algorithm:rllab and TabulaRL,使用 first-order implementation of Trust Region Policy Optimization (TRPO),同時To reduce variance in the stochastic gradient estimation, we use a baseline which is also represented as an RNN using GRUs as building blocks. We optionally apply Generalized Advantage Estimation (GAE).
-
hidden activation: relu
-
all weights matrices use weight normalization without data-dependent initialization
-
hidden to hidden weight: orthogonal initializaion
-
other weight: Xavier initialization
-
bias: 0
-
the policy and the baseline uses separate neural networks with the same architecture until the final layer, where the number of outputs differ.
MULTI-ARMED BANDITS

TABULAR MDPS
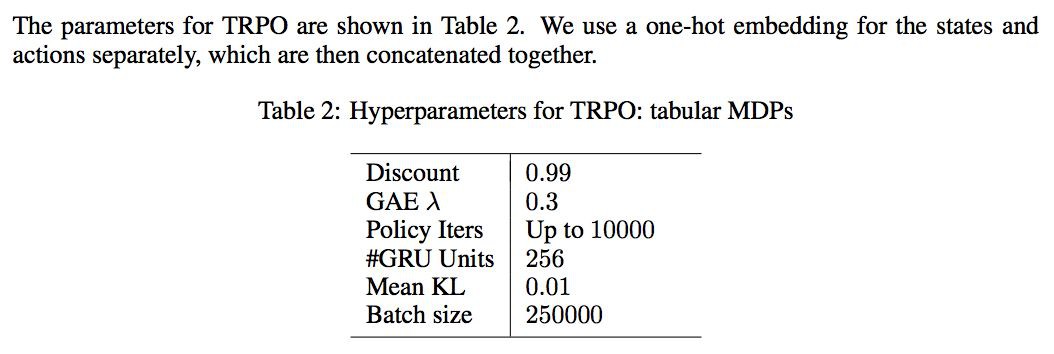
VISUAL NAVIGATION
-
40 x 30 RGB image, range [-1, 1]
-
2 層 Conv:16 個 filter, size 5 x 5, stride 2
-
將 action embedded 到 256-dimensional vector,然後與 2 的輸出 flattened 後拼接
-
256 hidden dense

左右互搏:self-play

■ 論文 | Emergent Complexity via Multi-Agent Competition
■ 連結 | https://www.paperweekly.site/papers/861
這篇文章給我們的最大啟發是,在實際工作中如何訓練一個比較複雜的 agent。
實驗效果蠻有趣的:
核心問題
1. 研究問題:在 MAS 環境下,如何穩定,有效地訓練一個具有複雜能力的 agent。
2. 假設條件:普通的 multiagent 假設,沒有中心式的 critic,independent training,不用知道對手的 action 和 policy。
3. 主要想法:利用 self-play 的思想,產生合適的對手。同時利用額外的 reward 來幫助學習 basic action。
4. 解決方案:設計 Exploration Curriculum,前期利用額外的 reward 來幫助學習基本 action,後期將這部分額外的 reward 衰減掉,讓 agent 能夠學習大宋真正希望學習的任務。使用 Opponent Sampling,避免對手一旦學的很好,使的自己的 agent 無法學習,無法收斂。
其實很多學科最終都是要實用,現在的 DRL 玩玩 Atari 的遊戲還好,但是面對更難的遊戲,比如星際二的時候,其實效果並不好,主要的原因是星際二的環境更複雜,我們需要學習出一個更複雜的 agent。
抽象地說環境的複雜性與學習出 skill 的複雜性是相關的,越複雜的環境就能學習出越複雜的 skill。但是我覺得複雜的話,有時候很難學,所以我們可能需要更多的工程上的努力。
不同的 single agent 的複雜性只與環境本身相關,比如你總不能讓一個普通 pixel 的 pong 的 agent 學出正手,反手擊球吧。
但是在 multiagent 的環境中,複雜性其實還與對手是相關的,比如圍棋,規則很簡單,但是你在和對手博弈的過程是十分複雜的。
圍棋的新手與高手有很大的區別,如果你讓你的 agent 一直與一個新手玩,這個 agent 可能最多就戰勝這個新手,但是實際上不會很厲害。
如果你讓你的 agent 一開始就和柯潔下,按照 RL 的學習方法,開始探索,然後慢慢學習,估計 agent 一盤都贏不了,最終什麼都沒有學到。
因此,如何在一個環境裡面學習到更複雜的策略、如何有效地進行學習才是本文的目的。
Exploration Curriculum
這裡假設環境都只在最後透過結果給予 agentreward(後面環境設定都是如此),那麼必然就帶來 reward 稀疏的問題。
一般的稀疏的 reward 的問題,透過隨機探索可以得到一定緩解,但是如果需要一些基本 basic 的行為,然後再做操作的任務,可能隨機探索就不是很好了。
比如一個經典的 HRL 的例子: 我們希望一個機器人移動到門邊,然後推開門,只有在推開門才給 reward。
描述很簡單,但是實際上機器人首先需要學習到控制 motor,透過控制 motor 來移動,然後才是導航,推門的動作。這樣的流程其實是比較複雜的,如果單純隨機的話,可能機器人只會在原地打滾。
因此就會有一個簡單的想法,透過額外的 reward 來幫助 agent 學習,比如獎勵移動,站立。那麼 agent 就容易獲得 dense 的 reward,學習到移動,站立。
但是這樣的在實際訓練中其實是不自然的,同時可能會影響,甚至損害 agent 在原先任務上的學習。比如:如果給予移動比較大的 reward,而出現成功開門的機率又比較小,那麼 agent 可能會被誘導成一直在移動的 agent。
那麼直觀地,我們肯定想要權衡兩者間的平衡,一種做法就是 Exploration Curriculum:在開始的時候給予 dense reward 來幫助學習,讓 agent 學習到一些 basic 的動作,比如移動,站立,同時可以幫助提高真正想學習任務 reward 出現的機率,這個 reward 被稱為 exploration reward。
隨著訓練,把 exploration reward 減少到 0,即不斷減小下麵的 αt ,所以只剩下真正任務的 reward,那麼接著學,最佳化的就是真正想要學習的任務了:

Opponent Sampling
正如上面說到的,太難對手,你太難學,太簡單的對手,你也學的菜。那麼該如何利用對手來學習出一個複雜的 task 的 policy 呢?
在實際學習的時候,可能出現一個 agent 先學的比較好,那麼另外一個 agent 可能完全學不到,或者不收斂,這種情況出現的比較多。也就是上面的:太難的對手出現的機率會多一些。
所以我們會想對手不要那麼難就好了,一種想法是:現在他比較難,但是他之前可能比較簡單啊!
這裡給了一個解決方案:就是在每個 rollout 開始的時候,選擇 random old version 的對手來學習。這樣的效果能學習得更穩定,策略更魯棒。
Note that for self-play this means that the policy at any time should be able to defeat random older versions of itself, thus ensuring continual learning.
Training Competitive Agents

這篇文章採用 distrubuted PPO 對 agent 做最佳化。
一個比較有價值的點是:PG 在 multiagent 的設定下更容易受到方差的影響而不穩定,為瞭解決這個不穩定的問題,MADDPG 用了一個中心式的 critic,但是這樣在訓練的時候就要求知道 global 的 state 和 joint action,加入了額外的限制條件。
但是用 independent 訓練時,又容易有方差的問題。為了緩解方差的問題,這裡的採用非常大的 batch size 的 distributed PPO 來做 independent 的 training。
因為大的 batch 包含的東西更多,agent 的 policy 稍微改變失誤就會對 PG 造成比較大影響,另外就是比較大的 batch 能夠包含更久的資訊,agent 不會特別快收斂當前的 policy,所以還能幫助探索。
兩個網路結構
MLP:兩個 128 個 unit 的 hidden layer(啟用函式沒有說)
LSTM:
-
128 個 unit 的全連線,使用 RELU
-
128 個 hidden state 的 LSTM
-
個數為 action dimension 的全連線
策略的細節
使用 Gaussian policy,其中 mean,diagonal covariance matrix 為網路的輸出,取樣後 clipped 到合理的 control range。
在 run-to-goal 和 you-shall-not-pass 中使用 MLP policy 與 value function,在 sumo 和 kick-and-defend 中使用 LSTM policy 與 value function(下麵會提到)。
主要的原因是 MLP 在使用 LSTM 那兩個任務不好。使用 LSTM 時,我們採用截斷的 BPTT,在 10 個 timesteps 採取截斷。
policy 與 value function 採用不同的引數,即不共享引數。
訓練細節
1. PPO 使用 clipped objective, ϵ=0.2,γ=0.995,λ=0.95。
2. 每個 agent 並行做多個 rollout,各自最佳化,collect 409600 samples from the parallel rollouts.
3. PPO training in mini-batches consisting of 5120 samples.
4. For MLP policies we did 6 epochs of SGD per iteration and for LSTM policies we did 3 epochs.
5. don’t use any entropy bonus,使用 L2。
6. 每個 agent 採用 4 個 GPU 來訓練。
5. 像 synchronous actor critic,在一整個 rollout 上計算 GAE,因為是在最後才給的 reward。
6. 最佳化器:Adam, lr 0.001
7. co-efficient αt in eq. 1 for the exploration reward is annealed to 0 in 500 iterations for all the environments except for kick-and-defend in which it is annealed in 1000 iterations.
Competitive Environments

agent 的 body 如下:
1. ant: 12 DoF,8 actuated joints
2. humanoid: 23 DoF,17 actuated joints 形狀如上圖
對於 ant body 的 observations:
all the joint angles of the agent its velocity of all its joints the contact forces acting on the body the relative position and all the joint angles for the opponent.
對於 humanoid body 的 observations:
在 ant body 的基礎上,centre-of-mass based inertia, mass, velocity and the actuator forces for the body.
四個環境:
1. run to goal:感覺就是方形的相撲,但其標的是到達另外一邊。先到達的 reward+1000,晚到達的 reward-1000,如果都沒有達到,那麼都 -1000。
2. you shall not pass:就是把 1 的內容稍作改動,標的是阻止對方到達對面。如果成功阻止了,而且最後成功阻止的 agent 還站著的話,阻止的 agent 的 reward+1000,如果阻止的 agent 沒有站著的話,它的 rewerd 為 0,然後那個被阻止的 agent reward 為 -1000。如果 agent 過去了,他的 reward 為 1000,這個阻止失敗的 agent reward 為 -1000。
3. sumo:就是相撲,圓形的場地,標的是讓對方摔倒或者推出場地。贏的獲得 +1000 的 reward,輸的獲得 -1000 的 reward。如果沒有輸贏,則都是 -1000。
4. kick and defend:射門。一個 agent 射門,一個 agent 防守。射門的地方有 6 個 unit 寬,成功的射門或者防守獲得 +1000,失敗的獲得 -1000。防守的 agent 不能離開球太遠,太遠的話,給予 -1000 的懲罰,另外如果防守成功,而且碰到球,再給予 +500 的獎勵,如果最後還站著,再給 +500。
對於相撲的環境,還有額外的 observations:
torso’s orientation vector the distance from the edge of the ring of all the agent the time remaining in the game.
對於點球的環境,還有額外的 observations:
the relative position of the ball from the agent the relative distance of the ball from goal the relative position of the ball from the two goal posts.
Experiments
使用 Exploration Curriculum 效果更好。

不同 opponent sampling 的影響,ant 一直都是均勻的好,因為 ant 簡單,random 的防守其實也不錯,但是 human 形狀的從一半開始取樣好,因為 human 更難,隨機不好。

另外為了驗證是否 over fitting 對手策略,這裡做了一個實驗就是踢球的環境,固定球訓練,然後在測試的時候移動球,發現 agent 不能很好的泛化,只在球的一個位置好:

但是開始一直隨機又學不好,因為空間太大,所以這裡類似 exploration reward的做法,開始小小的隨機,隨著訓練隨機形增大。
△ 戳我領取新年禮物
參與方式
1. 長按識別下方二維碼參與投票
2. 文末留言你喜歡某篇論文的原因
3. 分享本文到朋友圈並截圖發至後臺
截止時間
2018年1月24日0點0分
福利清單
PaperWeekly定製手機殼 x 3份
PaperWeekly定製筆記本 x 5份
PaperWeekly定製行李牌 x 10份

△ 我們長這樣哦~
長按掃描二維碼,參與投票!
▼

 # 高 能 提 醒 #
# 高 能 提 醒 #
1. 為了方便大家在投票過程中檢視論文詳情,請勿使用微信內建瀏覽器。點選頁面右上角的“…”按鈕,在手機瀏覽器中開啟表單。
2. 本次評選包含自然語言處理和計算機視覺兩大方向,請在你所選擇的參與方向下勾選3-10篇論文。
3. 獲獎名單將於1月25日公佈,其中5位由小編根據文末留言選取,其他13位採用隨機抽取,禮物隨機發放。
長按掃描二維碼,馬上投票!
▼

關於PaperWeekly
PaperWeekly 是一個推薦、解讀、討論、報道人工智慧前沿論文成果的學術平臺。如果你研究或從事 AI 領域,歡迎在公眾號後臺點選「交流群」,小助手將把你帶入 PaperWeekly 的交流群裡。

▽ 點選 | 閱讀原文 | 檢視作者知乎主頁
 知識星球
知識星球
