最近,知名博主 @drdrxp (張炎潑) 一條關於SlimTrie介紹的微博引發了熱議

高可用架構聯絡了 XP 老師,透過本文首次介紹了 SlimTrie 的詳細實現。本文作者李文博,吳義譜、張炎潑對本文亦有貢獻。
 李文博,目前就職於白山雲科技有限公司,從事雲儲存研發工程師。在白山主要有 s2 分散式物件儲存系統的日常建設和 ec 冷資料儲存叢集開發的實戰經歷,在分散式儲存服務方向有一些積累和經驗。
李文博,目前就職於白山雲科技有限公司,從事雲儲存研發工程師。在白山主要有 s2 分散式物件儲存系統的日常建設和 ec 冷資料儲存叢集開發的實戰經歷,在分散式儲存服務方向有一些積累和經驗。
 吳義譜,目前就職於白山CWN雲儲存部門,2016年加入白山,主要負責分散式物件儲存的研發工作,熟悉瞭解行業內主流的分散式儲存系統,積累了豐富的雲儲存相關技術,並運用這些技術攻剋了實際中遇到的難點,運用EC(Erasure Code)技術解決了冷資料在保證可靠性的同時降低33%成本,運用haystack技術解決百億級別小檔案的訪問IO瓶頸問題,運用paxos技術解決幾十億叢集管理和leader選舉問題。
吳義譜,目前就職於白山CWN雲儲存部門,2016年加入白山,主要負責分散式物件儲存的研發工作,熟悉瞭解行業內主流的分散式儲存系統,積累了豐富的雲儲存相關技術,並運用這些技術攻剋了實際中遇到的難點,運用EC(Erasure Code)技術解決了冷資料在保證可靠性的同時降低33%成本,運用haystack技術解決百億級別小檔案的訪問IO瓶頸問題,運用paxos技術解決幾十億叢集管理和leader選舉問題。
 張炎潑 (xp),30 年軟體開發經驗,物理系背叛者,設計師眼中的美工,bug maker,vim 死飯,懸疑片腦殘粉。曾就職新浪, 美團。現在白山雲,不是白雲山 。
張炎潑 (xp),30 年軟體開發經驗,物理系背叛者,設計師眼中的美工,bug maker,vim 死飯,懸疑片腦殘粉。曾就職新浪, 美團。現在白山雲,不是白雲山 。
上一篇 SlimTrie 設計篇 [1] 中,我們介紹了單機百億檔案的索引設計思路,今天我們來具體介紹下它程式碼級別的實現。文中我們要解決的問題是: 在一臺通用的100TB的儲存伺服器的記憶體中, 索引100億個小檔案。
而最終我們透過SlimTrie對儲存系統中靜態檔案的索引, 記憶體開銷只佔 Btree的 13%, 查詢速度卻是 Btree 的 2.6倍!
索引的一點背景知識
索引可以被認為是業務資料(使用者檔案)之外的一些”額外”的資料, 在這些額外的資料幫助下, 可以在大量的資料中快速找到自己想要的內容. 就像一本數學課本的2個”索引”: 一個是目錄, 一個是關鍵詞索引.現實系統中,儲存系統中的索引需要做到:
- 足夠小 : 一般實現為將索引資訊全部儲存在記憶體中可以達到比較好的效能。訪問索引的過程中不能訪問磁碟, 否則延遲變得不可控(這也是為什麼leveldb或其他db在我們的設計中沒有作為索引的實現來考慮).
- 足夠準確 : 對較小的檔案, 訪問一個檔案開銷為1次磁碟IO操作。
分析下已有的2種索引型別, hash-map型別的和tree型別的,Hash map類索引利用hash函式的計算來定位一個檔案:
- 優勢 :快速,一次檢索定位資料。非常適合用來做 單條 資料的定位。
- 劣勢 :無序。不支援範圍查詢。必須是等值匹配的,不支援“>”、“
- 記憶體開銷: O(k * n)。
- 查詢效率: O(k)。
而基於Tree 的索引中代表性的有: B+tree, RBTree, SkipList, LSM Tree, 排序陣列 :
- 優勢 : 它對儲存的key是排序的;
- 劣勢 : 跟Hash map一樣, 用Tree做索引的時候, map.set(key = key, value = (offset, size)) 記憶體中必須儲存完整的key, 記憶體開銷也很大: O(k * n);
- 記憶體開銷: O(k * n);
- 查詢效率: O(k * log(n));
以上是兩種經典的索引都存在一個無法避免的問題: key的數量很大時,它們對記憶體空間的需求會變的非常巨大:O(k * n) 。
如果100億個key(檔案名)長度為1KB的檔案。那麼僅這些key的索引就是 1KB * 100億 = 10,000GB。導致以上的經典資料結構無法將索引快取在記憶體中。而索引又必須避免訪問磁碟IO,基於這些原因我們實現了一套專為儲存系統設計的SlimTrie索引.
索引資料大小的理論極限
如果要索引n個key, 那每條索引至少需要 log 2 (n) 個bit的資訊, 才能區分出n個不同的key. 因此理論上所需的記憶體空間最低是log 2 (n) * n * n, 這個就是我們空間最佳化的標的. 在這裡, 空間開銷僅僅依賴於key的數量,而不會受key的長度的影響!
我們在實現時將所有要索引的key拆分成多組,來限制了單個索引資料結構中 n的大小, 這樣有2個好處:
- n 和 log 2 (n) 都比較確定, 容易進行最佳化;
- 佔用空間更小, 因為: a * log(a) + b * log(b)
SlimTrie索引結構的設計
我們最終達到每個檔案的索引平均記憶體開銷與key的長度無關, 每條索引一共10 byte, 其中:
- 6 byte是key的資訊;
- 4 byte是value: (offset, size); // value的這個設定是參考通常的儲存實現舉的一個例子,不一定是真實生產環境的配置。
實現思路:從Trie開始
在研究Trie索引的時候, 我們發現它的空間複雜度(的量級)、順序性、查詢效率(的量級)都可以滿足預期, 雖然實現的儲存空間開銷仍然很大,但有很大的最佳化空間。
Trie 就是一個字首樹, 例如,儲存了8個key(”A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, and “inn”)的Trie的結構如下:

Trie的特點在於原生的字首壓縮, 而Trie上的節點數最少是O(n), 這在量級上跟我們的預期一致。但Trie仍然需要每個節點都要儲存若干個指標(指標在目前普遍使用的64位系統上單獨要佔8位元組)。
SlimTrie的設計標的
功能要求:
- SlimTrie能正確的定位存在的key,但不需要保證定位不存在的key。
- SlimTrie支援範圍定位key。
- SlimTrie的記憶體開銷只與key的個數n相關,不依賴於key的長度k 。
- SlimTrie查詢速度要快。
限制:
- SlimTrie只索引靜態資料。 資料生成之後在使用階段不修改, 依賴於這個假設我們可以對索引進行更多的最佳化。
- SlimTrie支援最大16KB的key 。
- SlimTrie在記憶體中不儲存完整的key的資訊。
最終 效能標的對比其他幾種常見的資料結構應是:
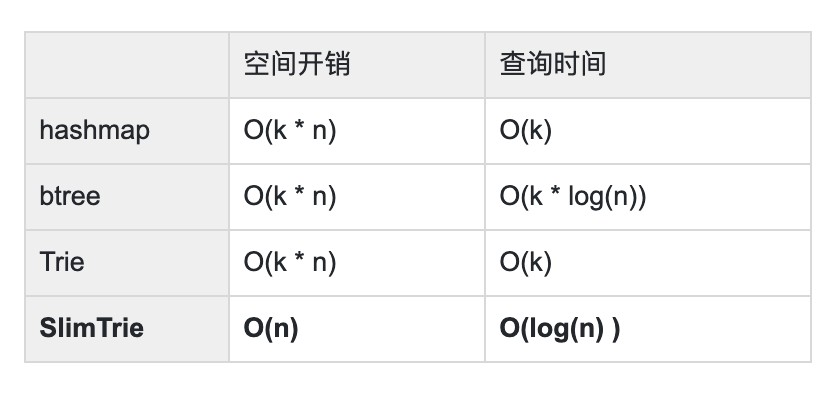
SlimTrie的術語定義
- key:某個使用者的檔案名,一般是一個字串。
- value: 要索引的使用者資料, 這裡value是一組(offset, size)。
- n: key的總數: <= 2 15 。
- k: key的平均長度 < 2 16 。
- Leaf 節點: SlimTrie中的葉子節點, 每個Leaf對應一個存在的key。
- LeafParent 節點:帶有1個Leaf節點的節點。 SlimTrie中最終Leaf節點會刪掉,只留下LeafParent節點。
- Inner 節點: SlimTrie中的Leaf和LeafParent節點之外的節點。
SlimTrie的生成步驟
我們透過一個例子來看看SlimTrie的生成: 如果一步步將Trie的儲存空間壓縮, 併在每一步處理後都驗證去掉某些部分後, 它仍然滿足我們的查詢的準確性要求. 然後在這個例子的基礎上,給出完整的演演算法定義。
SlimTrie的生成分為3部分:
1. 先用一個Trie來構建所有key的索引。
2. 在Trie的基礎上進行裁剪, 將索引資料的量級從O(n * k)降低到O(n)。
3. 透過3個compacted array來儲存整個Trie的資料結構, 將記憶體開銷降低。
1 SlimTrie原始Trie的建立
假設有一組排序的key用來構建索引:”abd”, “abdef”, “abdeg”, “abdfg”, “b123”, “b14”,首先建立一個標準的Trie:

查詢遵從標準的Trie的查詢流程:
例如從Trie中查詢”abdfg”,首先定位到根節點,然後從查詢key中取出第1個字元”a”, 在根節點上找到一個匹配的分支”a”,定位到第2層節點”a”,再從被查詢的key中取出第2個字元”b”,匹配第2層中節點”a”的分支”b”,依次向下,直到遇到一個Leaf節點,結束查詢。
2 SlimTrie的裁剪
基於SlimTrie的設計可以看出: 多分支的SlimTrie節點是關鍵的 ,單分支的節點對定位一個存在的key沒有任何幫助。所以可以針對節點型別,進行幾次單分支節點的裁剪。
並且在每次剪裁後,我們會依次展示剪裁過的Trie依舊滿足我們設計標的中對查詢的功能需要。
LeafParent節點的裁剪
上圖中,”abdfg”中的”g”節點不需要保留, 因為存在的key的字首如果是”abdf”, 它最後1個字元只能是”g”,所以將”abdfg”的”g”去掉。
同理,”b123”中的”3”也去掉。得到裁剪之後的結果:

圖中使用正則運算式的風格表示路徑:
“.” 代表任意字元; “{1}” 代表1個; ”f.{1}“ 代表f後面越過(Step)一個字元。
剪掉單分支LeafParent節點後依舊滿足查詢需求:
還以查詢key ”abdfg”為例,假設目前定位到節點”abd”,要繼續查詢key中的字元”f”,發現Trie中有分支”f”,並且”f”之後的可以略過”g”的查詢,則查詢直接定位到”abdf.”節點,查詢結束。
Inner 節點的裁剪
繼續觀察上圖, a分支下的”b”, “d”節點是不需要的, 因為一個存在的key如果以”a”開頭, 它的接下來的2個字元一定是”b”, “d”,同樣b節點後面去掉1分支,得到第2次 裁剪後的結果:
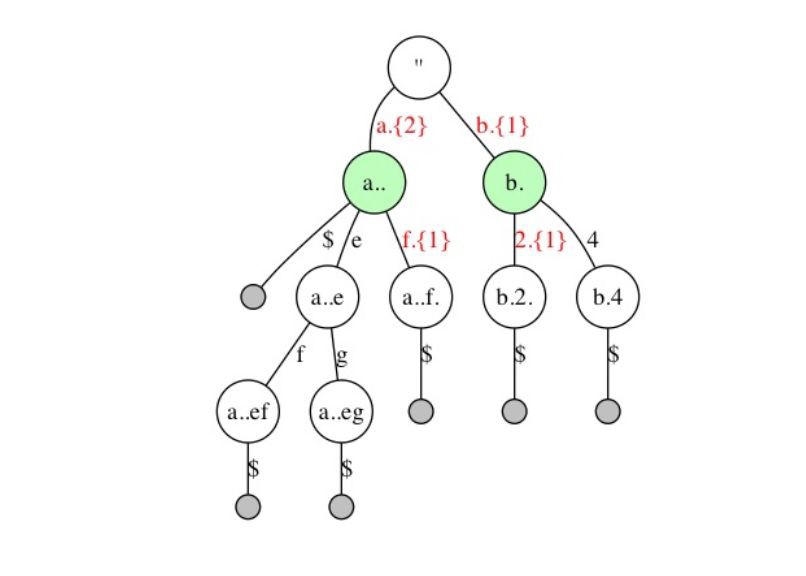
剪掉單分支Inner節點後依舊滿足查詢需求:
繼續以查詢”abdfg”為例,假設開始查詢,定位到根節點,要查詢key中第1個字元”a“,根節點有1個分支”a”與之匹配,並且可以越過2個字元,此時查詢定位到節點”a..”上,並繼續查詢key的第3個字元”f”,最終也定位到節點”a..f.”上。查詢結束。
去掉尾部Step
最後,去掉所有單分支LeafParent節點節點字尾,以及指向這個節點的路徑的Step數(例如“a..f.”和“b.2.”中尾部被Step掉的字元不需要記錄。但同時包含分支的LeafParent節點需要保留Step數,例如“a..”,指向它的分支“a.{2}”中的Step數還必須記錄)

去掉LeafParent節點的Step數後 依舊滿足查詢需求 :
當查詢一個存在的key:”abdfg”時,假設定位到了“a..”節點(對應查詢字串中的”abd“),繼續查詢下一個字元”f“時,因為key”abdfg”是存在於Trie中的,所以被查詢的key中f後面剩下的字元數(1個”g“)跟分支“f.{1}”中記錄的需要Step掉的字元數一定是相等的,所以當查詢到節點”a..f”時,發現它是1個LeafParent節點,則直接略過被查詢key中剩餘的字元。最終結束查詢。
裁剪之後的SlimTrie:
- 每個節點都有大於1個子節點, 除LeafParent節點之外。
- SlimTrie的大小跟key的長度無關. 也就是說任意長度的key的集合都可以使用有限大小的SlimTrie來索引: SlimTrie最多有2n-1個節點: 最多節點是出現在所有inner節點都是二分的時候(空間複雜度為O(n))
3 SlimTrie的壓縮
現在我們在結構上已經將SlimTrie裁剪到最小, 接下來還要在實現上壓縮SlimTrie實際的記憶體開銷。樹形結構在記憶體中多以指標的形式來實現, 但指標在64位系統上佔用8個位元組, 相當於最差情況下, 記憶體開銷至少為 8*n個位元組,這樣的記憶體開銷還是太大了,所以我們使用2個約束條件來壓縮記憶體開銷:
- key的個數n:n <2 15;目的是透過id來替代指標,將節點id值限制在16bit內。節點id分配規則是:從根節點開始,逐層向下,按照節點從左到右的順序編號。
- 4 bit的word:建立Trie時,將每個長度為k的字串,視為2 * k個4 bit的word,而不是k個8 bit的byte,作為SlimTrie上節點的單位。這樣做的目的是減少分支數量,限制儲存分支資訊的bitmap的大小。
另外為了更具體的說明這個例子,我們假設value是1個4 byte的記錄, 來展示SlimTrie中每個節點對應的資訊,其中只有 綠色 是需要記錄的, 如下圖:
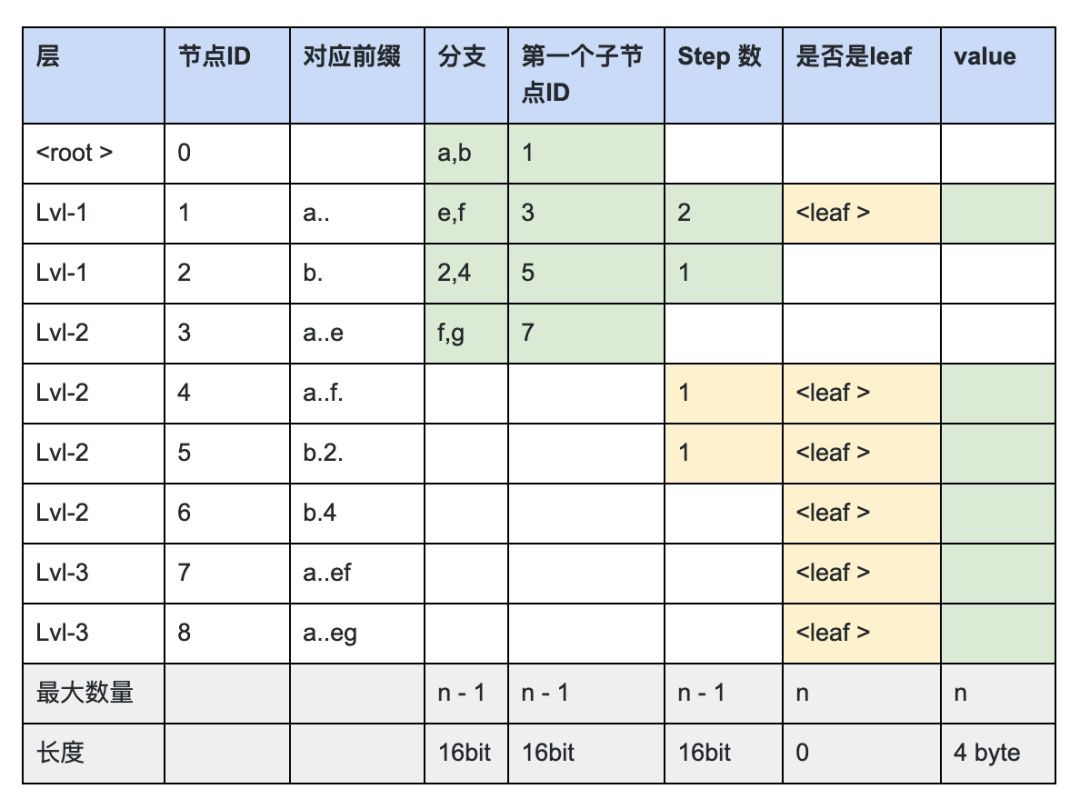
上面的表格中, 因為1個節點”是否leaf“的資訊跟”是否有value“是對等的,所以leaf資訊不需要記錄。而最終的索引需要的 總儲存量是:
分支資訊 + 子節點位置 + Step 資訊 + value
總共小於: 16bit * (n-1) + 16bit * (n-1) + 16bit * (n-1) + 4byte * n;
因此總儲存量小於 10 * n byte;其中去掉4 * n 個byte的value資訊, 大約每個Key 6位元組 。 接下來我們來解釋下如何在實現上達成6 位元組這個標的:
SlimTrie內部的 資料結構
透過上面的表格我們看到,如果要完整的表達SlimTrie的結構,需要儲存4個對映表:
- uint16 id → uint16 branch
每個節點的分支有哪些; 因為使用了4 bit的word, 所以每個節點最多隻有16個分支,每個節點的分支表使用一個16 bit的bitmap儲存;
- uint16 id → uint16 offset
每個節點的第一個子節點id;
- uint16 id → uint16 step
每個節點被查詢到之後需要越過源查詢key後面幾個word; 因為key的最大長度設定為16 KB,所以step最大是2 * 16 KB = 2 15;
- uint16 id → uint32 value
實際儲存的資料,也同時表示了是否是LeafParent節點;
把SlimTrie抽象成這幾個對映表後,所需的資料結構 就變得清楚了:
整數作為下標,整數為元素的陣列,例如 branch可以定義為 uint16_t branch[n]。但是,並不是每個節點id都存在分支,這個陣列中很多位置是空的。如果用陣列來儲存會造成一半的空間浪費(Inner節點數量最多隻佔一半)。所以我們需要一個更加緊湊的資料結構來儲存這幾個對映表,這裡我們引入了一個資料結構:compacted array。
compacted array:壓縮陣列
compacted array類似陣列,但不為 不存在 的陣列元素分配空間。在實現上,為了標識空的陣列元素,使用了1個bitmap,雖然每個要儲存的資訊平均多分配了1個bit,但整體空間開銷非常接近於我們的預期。
使用壓縮陣列來儲存SlimTrie的邏輯結構, 壓縮陣列用來儲存最大大小不超過2 16 個條目的資訊,首先定義壓縮陣列的結構:
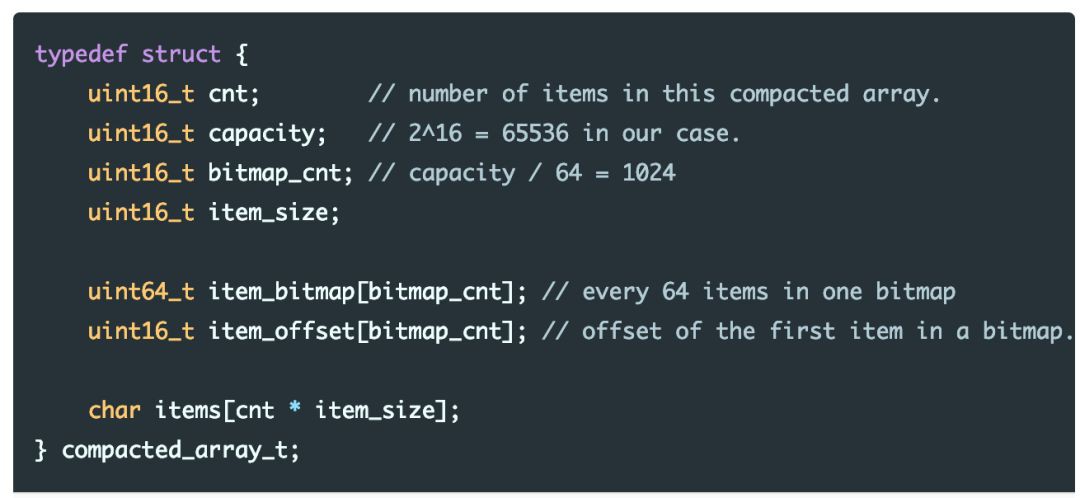
因為我們使用16 bit的id代替指標, 這就要求每個組裡的節點(node)數量不能超過65536(2 16),由於SlimTrie生成時會產生至多 n-1 個中間節點(在滿二叉的情況下總結點數是 2n-1), 所以我們需要限制每個組的原始資料條目數n 小於2 15 =3 2768。
compacted array的記憶體額外開銷
除了資料items陣列之外,每個compacted array的額外資料包括:
4個 uint16 的成員屬性,以及跟元素總數相關的bitmap 和 offset,分別佔(n / 64) * 8 byte 和 (n / 64) * 2 byte;
於是每個compacted array的總的記憶體額外開銷是 (0.15 * n + 8) byte;
到這裡,可以近似認為SlimTrie的空間開銷是(6 * 1.15 * n + 24) byte。
對於SlimTrie,我們只需要3個compacted array來儲存其結構:內部節點(inners),使用者資料(LeafParent)和Step資訊:
inners陣列:
inners的每個元素是4 byte, 其中2 byte是一個bitmap來儲存最多15個子節點的branch. 另外一個2 byte的uint16表示它第一個子節點id(offset),因為一個節點的所有子節點id是連續的,所以只需要儲存第一個子節點。
在訪問SlimTrie時, branch_bitmap和第一個子節點的id(offset),幾乎所有的情況下都需要同時對其訪問,因此把他們放到一個compacted array中,減少compacted array查詢的次數(雖然查詢開銷不大,但我們也非常關註每個點的最佳化!)。
LeafParent陣列:
LeafParent的一個item儲存4 byte的使用者資料value 。
Step陣列:
Step陣列中的每個元素是單分支節點裁剪掉的節點數,使用一個2 btye的uint16表示。
最終SlimTrie的所有資訊在記憶體中的組織方式如下:

記憶體開銷分析
假設 :
- 共有n個key,也就是LeafParent節點(或value)的個數;
- 每個value是4位元組 ;
- 至多存在n – 1個Inner節點;(全二分時最多)
- 並且Step 只存在於指向Inner節點的分支,因此最多也是n – 1個;
再考慮compacted array的額外開銷,最終整體的記憶體開銷如下:

在儲存系統 中使用SlimTrie作為資料索引的場景裡, 如果用 32G記憶體, 大約可以索引32億個檔案。
SlimTrie的查詢實現
SlimTrie的查詢類似於普通Trie的查詢,在建立過程中已經逐步描述了查詢在裁剪之後的Trie中的處理方式, 現在將整個過程統一用下麵這個c語法的偽程式碼來描述查詢過程,其中幾個函式get_value,get_branches,get_step實際上會透過compacted array的”get”操作來訪問SlimTrie的3個對映表來實現。
其中src是1個4 bit word的陣列:

索引合併最佳化
到目前為止索引的空間利用率已經非常高了,但是,它還是一個不安全的設計!因為它沒有給出一個最壞情況保證:如果檔案超過32億個怎麼辦?如果出現了超出的情況,最好的結果恐怕也是記憶體開始使用swap,系統反應變慢3個數量級。
因此我們需要對演演算法給出一個穩定下界,妥善處理超多檔案的情況, 所以可以在準確度和記憶體開銷方面做一個折中:這裡有一個假設是, 磁碟的一次IO, 開銷是差不多的, 跟這次IO的讀取的資料量大小關係不大,所以可以在一次IO中讀取更多的資料來有效利用IO :
對一個存在的key, 我們的索引將傳回一個磁碟上的offset, 我們一定可以在這個offset和之後的64KB的磁碟空間上找到這個檔案,也就是說, 我們的索引不允許索引過小的檔案, 只將檔案的位置定位到誤差64KB的範圍內。
最差情況是全部檔案都是小檔案(例如10K, 1K), 這時索引個數 = 100T / 64KB =~ 20億條。按照每條索引10 位元組計算,需要20GB記憶體空間。
SlimTrie索引的記憶體開銷測試
首先我們用一個基本的實驗來證明我們實現的記憶體開銷和上文說到的理論是相符的。實驗選取Hash 類資料結構的map 和 Tree 類資料結構的B-Tree 與 SlimTrie 做對比,計算在同等條件下,各個資料結構建立索引所佔用的記憶體空間。
實驗在go語言環境下進行,map 使用 golang 的 map 實現,B-Tree使用Google的BTree implementation for Go ( https://github.com/google/btree ) 。 key 和 value 都是 string 型別(我們更多關心它的大小而不是型別)。實驗的結果資料如下 :

上圖中可以看到:
- SlimTrie 作為索引在記憶體的節省上碾壓 map 和 B-Tree。
- SlimTrie 作為索引其記憶體佔用的決定因素是 key的數量,與key的大小無關。
SlimTrie 作為Key-Value map的記憶體開銷測試
看過以上比較,SlimTrie 似乎勝得過於輕鬆,其根本原因是 SlimTrie “開掛” 似地縮減了索引的 key 的空間。這一點上面也提到了,SlimTrie 作為索引有一個前提約束是,索引只提供完整的 value 資訊而不提供 key 的資訊。這一點在作為資料定位的索引時,是可以接受的,也正是因為這一點 SlimTrie 在和 map 的記憶體佔用比較中得以大獲全勝。
現在如果拋開 “索引” 這個用處,在通用場景下,讓SlimTrie作為索引, 同時也記錄完整的key的資訊, 將他實現為一個通用的key-value map, 看看 SlimTrie 這個資料結構的效能。這裡需要將 key + value 當做 SlimTrie 的一個 value 去使用就可以做到。
此次試驗,我們同樣選取了幾組 key 和 value 的大小,在 同之前一樣的 go 語言環境下進行了測試,SlimTrie 的 value 是這樣一個結構:

因為這次測試所有的資料結構都儲存了完整的key和value資訊,所以我們只看memory overhead(除了key, value本身資料之外, 額外需要的空間)。測試得到的資料,見下麵的圖表:
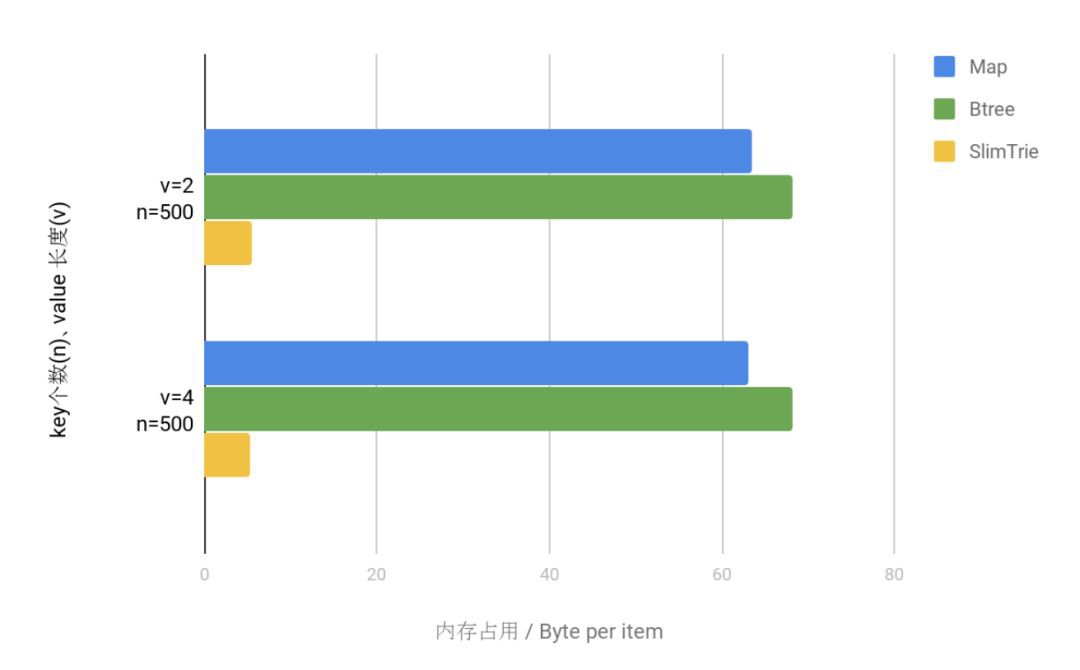
兩者進行對比,可以明顯看出,SlimTrie 所佔用的空間額外開銷仍然遠遠小於 map 和 B-Tree 所佔的記憶體,在 map 和 btree 中, 每個 key 能夠節省大約 50 Byte, 而SlimTrie是6位元組左右 .
SlimTrie的查詢效能測試
記憶體佔用空間大獲全勝之後,我們還對 SlimTrie 的查詢進行了測試,同時與 map 、Btree 進行了比較。在與記憶體測試相同的go語言環境下進行實驗。為了公平也同樣對比的是SlimTrie實現的key-value map跟 golang map, btree的效能對比.
存在的 key 的查詢效率對比
越小越優:

不存在的 key 的查詢效率對比
越小越優:

可以看出 SlimTrie 的查詢效率與 無序的hash型別的Map 相比有差距, 但對比同樣是保持了順序性的btree相比, 效能是Btree的 2.6倍 左右.
查詢時間隨k和n的變化

另一方面,在上圖中,我們也能夠看到,SlimTrie 的實際查詢的耗時在 150ns 左右,加上優秀的空間佔用最佳化,作為儲存系統的索引依然有非常強的競爭力。
記憶體開銷隨k和n的變化

上圖中我們可以看出, 不論是隨著key的數量增大或是key的長度變長, 單條索引的記憶體開銷都非常穩定地保持在6~7個位元組範圍內。
總結
SlimTrie 為未來而生。當下資訊爆炸增長,陳舊的索引樣式已無法適應海量資料新環境,儲存系統海量資料的元資訊管理面臨巨大挑戰,而SlimTrie 提供了一個全新的解決方法,為海量儲存系統帶來一絲曙光,為雲儲存擁抱海量資料時代註入了強大動力,讓我們看到了未來的無限可能。
作為索引,SlimTrie 的優勢巨大,可以在10GB記憶體中建立1PB資料量的索引,空間節約驚人,令以往的索引結構望塵莫及;時間消耗上,SlimTrie 的查詢效能與 sorted Array 接近,超過經典的B-Tree。拋下索引這個身份,SlimTrie 在各項效能方面表現依舊不俗,作為一個通用 Key-Value 的資料結構,記憶體額外開銷仍遠遠小於經典的 map 和 Btree 。
SlimTrie 不僅為我們解決了眼前的困境,也讓我們看到了未來的可能。它的成功不會停下我們開拓的腳步,這隻是個開始,還遠沒有結束。
參考連結:
1. https://openacid.github.io/tech/algorithm/slimtrie-design
2. https://github.com/openacid/slim (專案地址)
本文作者李文博,吳義譜、張炎潑對本文亦有貢獻。轉載本文請註明出處,GIAC全球網際網路架構大會深圳站將於2019年6月舉行,屆時將有系統最佳化等專題深入探討相關話題,敬請期待。
 知識星球
知識星球
