(點選上方公眾號,可快速關註)
轉自:melonstreet
http://www.cnblogs.com/QG-whz/p/5173112.html
二叉堆的定義
二叉堆是一種特殊的堆,二叉堆是完全二叉樹或近似完全二叉樹。二叉堆滿足堆特性:父節點的鍵值總是保持固定的序關係於任何一個子節點的鍵值,且每個節點的左子樹和右子樹都是一個二叉堆。
當父節點的鍵值總是大於或等於任何一個子節點的鍵值時為最大堆。 當父節點的鍵值總是小於或等於任何一個子節點的鍵值時為最小堆。
二叉堆的儲存
二叉堆一般使用陣列來表示。請回憶一下二叉樹的性質,其中有一條性質:
性質五:如果對一棵有n個節點的完全二叉樹的節點按層序編號(從第一層開始到最下一層,每一層從左到右編號,從1開始編號),對任一節點i有:
1、如果i=1 ,則節點為根節點,沒有雙親。
2、如果2 * i > n ,則節點i沒有左孩子 ;否則其左孩子節點為2*i . (n為節點總數)
3、如果2 * i+1>n ,則節點i沒有右孩子;否則其右孩子節點為2*1+1.
簡單來說:
1、如果根節點在陣列中的位置是1,第n個位置的子節點分別在2n 與 2n+1,第n個位置的雙親節點分別在⌊i /2⌋。因此,第1個位置的子節點在2和3.
2、如果根節點在陣列中的位置是0,第n個位置的子節點分別在2n+1與2n+2,第n個位置的雙親節點分別在⌊(i-1) /2⌋。因此,第0個位置的子節點在1和2.
得益於陣列的隨機儲存能力,我們能夠很快確定堆中節點的父節點與子節點。
下麵以大頂堆展示一下堆的陣列儲存。

在本文中,我們以大頂堆為例進行堆的講解。本文大頂堆的根節點位置為0.
二叉堆的具體實現
在二叉堆上可以進行插入節點、刪除節點、取出堆頂元素等操作。
二叉堆的抽象資料型別
/*大頂堆類定義*/
template <typename T>
class MaxHeap
{
public:
bool insert(T val); //往二叉堆中插入元素
bool remove(T data); //移除元素
void print(); //列印堆
T getTop(); //獲取堆頂元素
bool createMaxHeap(T a[], int size);//根據指定的陣列來建立一個最大堆
MaxHeap(int cap = 10);
~MaxHeap();
private:
int capacity; //容量,也即是陣列的大小
int size; //堆大小,也即是陣列中有效元素的個數
T * heap; //底層的陣列
private:
void filterUp(int index); //從index所在節點,往根節點調整堆
void filterDown(int begin ,int end ); //從begin所在節點開始,向end方向調整堆
};
1、註意capacity與size的區別。capacity指的是陣列的固有大小。size值陣列中有效元素的個數,有效元素為組成堆的元素。
2、heap為陣列。
二叉堆的插入
在陣列的最末尾插入新節點,然後自下而上地調整子節點與父節點的位置:比較當前結點與父節點的大小,若不滿足大頂堆的性質,則交換兩節點,從而使當前子樹滿足二叉堆的性質。時間複雜度為O(logn)。
當我們在上圖的堆中插入元素12:
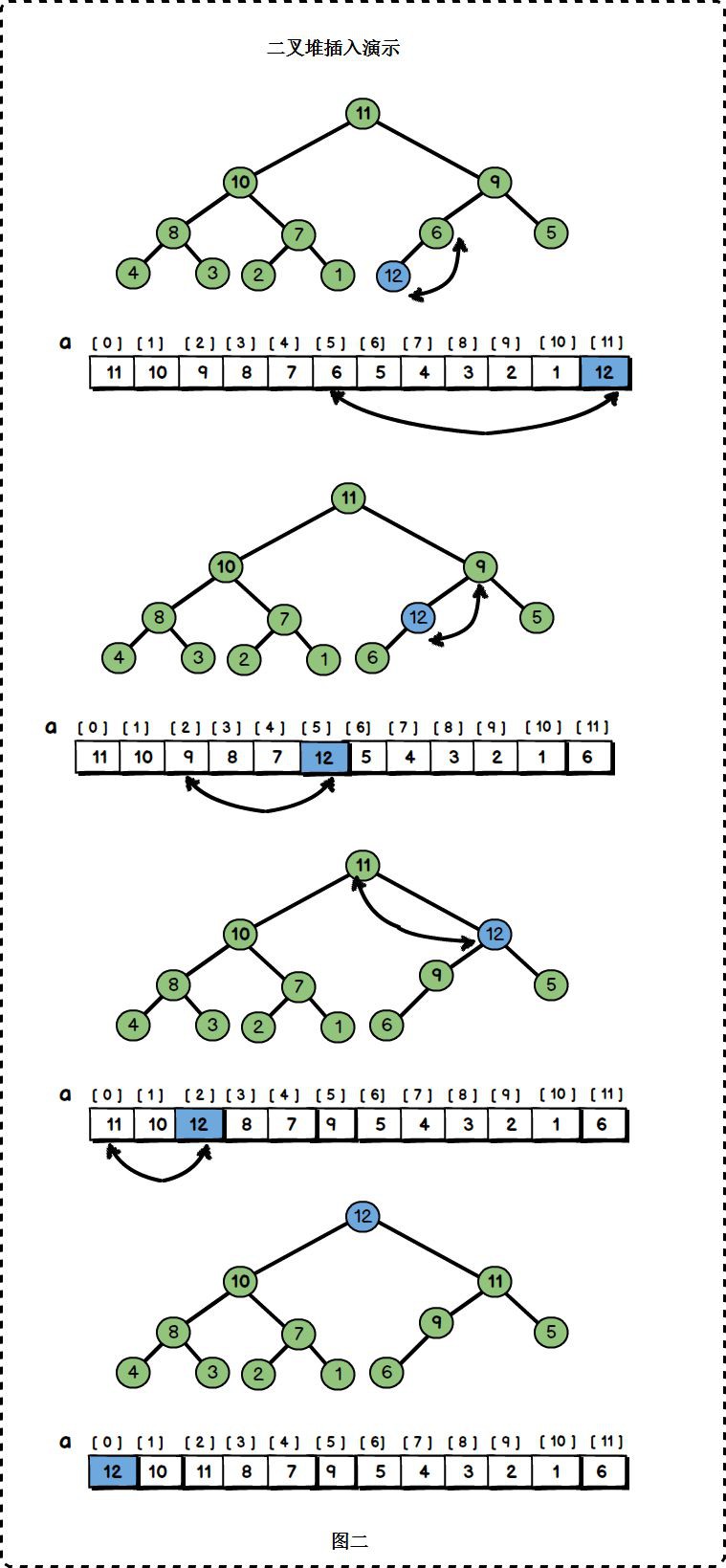
調整過程:
1、節點12新增在陣列尾部,位置為11;
2、節點12的雙親位置為⌊11/2⌋ = 5,即節點6;節點12比節點6大,與節點6交換位置。交換後節點12的位置為5.
3、節點12的雙親位置為⌊ 5 /2⌋ = 2,即節點9;節點12比節點9大,與節點9交換位置。交換後節點12的位置為2.
4、節點12的雙親位置為⌊2/2⌋ = 1,即節點11;節點12比節點11大,與節點11交換位置。交換後節點12的位置為1.
5、12已經到達根節點,調整過程結束。
這個從下到上的調整過程為:
/*從下到上調整堆*/
/*插入元素時候使用*/
template <typename T>
void MaxHeap<T>::filterUp(int index)
{
T value = heap[index]; //插入節點的值,圖中的12
while (index > 0) //如果還未到達根節點,繼續調整
{
int indexParent = (index –1)/ 2; //求其雙親節點
if (value< heap[indexParent])
break;
else
{
heap[index] = heap[indexParent];
index = indexParent;
}
}
heap[index] = value; //12插入最後的位置
};
在真正程式設計的時候,為了效率我們不必進行節點的交換,直接用父節點的值改寫子節點。最後把新節點插入它最後的位置即可。
基於這個調整函式,我們的插入函式為:
/*插入元素*/
template <typename T>
bool MaxHeap<T>::insert(T val)
{
if (size == capacity) //如果陣列已滿,則傳回false
return false;
heap[size] = val;
filterUp(size);
size++;
return true;
};
二叉堆的刪除
堆的刪除是這樣一個過程:用陣列最末尾節點改寫被刪節點,再從該節點從上到下調整二叉堆。我們刪除根節點12:

可能有人疑惑,刪除後陣列最末尾不是多了一個6嗎?
的確,但我們把陣列中有效元素的個數減少了一,最末尾的6並不是堆的組成元素。
這個從上到下的調整過程為:
/*從上到下調整堆*/
/*刪除元素時候使用*/
template<typename T>
void MaxHeap<T>::filterDown(int current,int end)
{
int child = current * 2 + 1; //當前結點的左孩子
T value = heap[current]; //儲存當前結點的值
while (child <= end)
{
if (child < end && heap[child] < heap[child+1])//選出兩個孩子中較大的孩子
child++;
if (value>heap[child]) //無須調整;調整結束
break;
else
{
heap[current] = heap[child]; //孩子節點改寫當前結點
current = child; //向下移動
child = child * 2 + 1;
}
}
heap[current] = value;
};
/*刪除元素*/
template<typename T>
bool MaxHeap<T>::remove(T data)
{
if (size == 0) //如果堆是空的
return false;
int index;
for (index = 0; index < size; index++) //獲取值在陣列中的索引
{
if (heap[index] == data)
break;
}
if (index == size) //陣列中沒有該值
return false;
heap[index] = heap[size – 1]; //使用最後一個節點來代替當前結點,然後再向下調整當前結點。
filterDown(index,size—);
return true;
};
其餘操作
其餘操作很簡單,不在這裡囉嗦。
/*列印大頂堆*/
template <typename T>
void MaxHeap<T>::print()
{
for (int i = 0; i < size; i++)
cout << heap[i] << ” “;
};
/*獲取堆頂元素*/
template <typename T>
T MaxHeap<T>::getTop()
{
if (size != 0)
return heap[0];
};
/*根據指定的陣列來建立一個最大堆*/
template<typename T>
bool MaxHeap<T>::createMapHeap(T a[], int size)
{
if (size > capacity) // 堆的容量不足以建立
return false;
for (int i = 0; i < size; i++)
{
insert(a[i]);
}
return true;
};
二叉堆程式碼測試
測試程式碼:
int _tmain(int argc, _TCHAR* argv[])
{
MaxHeap<int> heap(11);
//逐個元素構建大頂堆
for (int i = 0; i < 10; i++)
{
heap.insert(i);
}
heap.print();
cout << endl;
heap.remove(8);
heap.print();
cout << endl;
//根據指定的陣列建立大頂堆
MaxHeap<int> heap2(11);
int a[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
heap2.createMaxHeap(a, 10);
heap2.print();
getchar();
return 0;
}
執行結果:
9 8 5 6 7 1 4 0 3 2
9 7 5 6 2 1 4 0 3
10 9 6 7 8 2 5 1 4 3
覺得本文有幫助?請分享給更多人
關註「演演算法愛好者」,修煉程式設計內功
 知識星球
知識星球