
過去幾年發表於各大 AI 頂會論文提出的 400 多種演演算法中,公開演演算法程式碼的僅佔 6%,其中三分之一的論文作者分享了測試資料,約 54% 的分享包含“偽程式碼”。這是今年 AAAI 會議上一個嚴峻的報告。 人工智慧這個蓬勃發展的領域正面臨著實驗重現的危機,就像實驗重現問題過去十年來一直困擾著心理學、醫學以及其他領域一樣。最根本的問題是研究人員通常不共享他們的原始碼。
可驗證的知識是科學的基礎,它事關理解。隨著人工智慧領域的發展,打破不可復現性將是必要的。為此,PaperWeekly 聯手百度 PaddlePaddle 共同發起了本次論文有獎復現,我們希望和來自學界、工業界的研究者一起接力,為 AI 行業帶來良性迴圈。
作者丨黃濤
學校丨中山大學數學學院18級本科生
研究方向丨影象識別、VQA、生成模型和自編碼器

論文復現程式碼:
http://aistudio.baidu.com/#/projectdetail/23600
GAN
生成對抗網路(Generative Adversarial Nets)是一類新興的生成模型,由兩部分組成:一部分是判別模型(discriminator)D(·),用來判別輸入資料是真實資料還是生成出來的資料;另一部分是是生成模型(generator)G(·),由輸入的噪聲生成標的資料。GAN 的最佳化問題可以表示為:

其中 Pdata 是生成樣本,noise 是隨機噪聲。而對於帶標簽的資料,通常用潛碼(latent code)c 來表示這一標簽,作為生成模型的一個輸入,這樣我們有:

然而當我們遇到存在潛在的類別差別而沒有標簽資料,要使 GAN 能夠在這類資料上擁有更好表現,我們就需要一類能夠無監督地辨別出這類潛在標簽的資料,InfoGAN 就給出了一個較好的解決方案。
互資訊(Mutual Information)
互資訊是兩個隨機變數依賴程度的量度,可以表示為:

要去直接最佳化 I(c;G(z,c)) 是極其困難的,因為這意味著我們要能夠計算後驗機率(posterior probability)P(c|x),但是我們可以用一個輔助分佈(auxiliary distribution)Q(c|x),來近似這一後驗機率。這樣我們能夠給出互資訊的一個下界(lower bounding):

InfoGAN
在 InfoGAN 中,為了能夠增加潛碼和生成資料間的依賴程度,我們可以增大潛碼和生成資料間的互資訊,使生成資料變得與潛碼更相關:
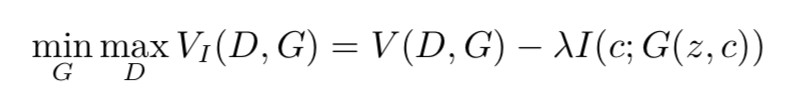

▲ 圖1. InfoGAN的整體結構圖
由上面的,對於一個極大化互資訊的問題轉化為一個極大化互資訊下界的問題,我們接下來就可以定義:

在論文的附錄中,作者證明瞭:

於是:

故 LI (G, Q) 是互資訊的一個下界。作者指出,用蒙特卡羅模擬(Monte Carlo simulation)去逼近 LI (G, Q) 是較為方便的,這樣我們的最佳化問題就可以表示為:

實現
在實現中,D(x)、G(z, c) 和 Q(x) 分別用一個 CNN (Convolutional Neural Networks)、CNN、DCNN (DeConv Neural Networks) 來實現。同時,潛碼 c 也包含兩部分:一部分是類別,服從 Cat(K = N,p = 1/N),其中 N 為類別數量;另一部分是連續的與生成資料有關的引數,服從 Unif(−1,1) 的分佈。
在此應指出,Q(c|x) 可以表示為一個神經網路 Q(x) 的輸出。對於輸入隨機變數 z 和類別潛碼 c,實際的 LI(G, Q) 可以表示為:

其中 · 表示內積(inner product),c 是一個選擇計算哪個 log 的引數,例如 ci = 1 而 cj = 0(∀j = 1,2,···,i − 1,i + 1,···,n),那麼 z 這時候計算出的 LI(G,Q) 就等於 log(Q(z,c)i)。這裡我們可以消去 H(c),因為 c 的分佈是固定的,即最佳化標的與 H(c) 無關:

而對於引數潛碼,我們假設它符合正態分佈,神經網路 Q(x) 則輸出其預測出的該潛碼的均值和標準差, 我們知道,對於均值 μ,標準差 σ 的隨機變數,其機率密度函式為:
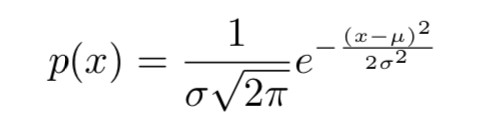
要計算引數潛碼 c 的 ,就是要計算 log p(c),即:
,就是要計算 log p(c),即:

設 Q(x) 輸出的引數潛碼 c 的均值 μ,標準差 σ 分別為 Q(x)μ 和 Q(x)σ,那麼對於引數潛碼 c:

同樣的,我們可以消去 H(c),因為 c 的分佈是固定的,那麼:

實驗
首先,透過和普通的 GAN 比較 LI ,作者證明瞭 InfoGAN 確實能夠最佳化這一互資訊的下界 2。
作者在 MNIST 手寫數字資料集(3)、3D 面部資料集(4)、3D 椅子資料集(5)、SVHN 街景房號資料集(6)以及 CelebA 人臉資料集(7)上進行了模型的相關測試。

▲ 圖2. MNIST手寫字元資料集上的結果

▲ 圖3. 3D面部資料集上的結果

▲ 圖4. 3D椅子資料集上的結果

▲ 圖5. SVHN街景房號資料集上的結果

▲ 圖6. CelebA人臉資料集上的結果
作者展示了這些資料集上學習到的類別潛碼(從上至下變化)和引數潛碼(從左至右變化,由 -2 到 2),我們可以看出,InfoGAN 不僅能夠很好地學習資料之間的型別差別,也能夠很好地學習到資料本身的一些易於區分的特點,而且生成模型對這些特點的泛化能力還是很好的。
再論InfoGAN的LI
讀完論文,我們發現,對於類別潛碼,這個 LI 本質上是 x 與 G(z, c) 之間的 KL 散度:
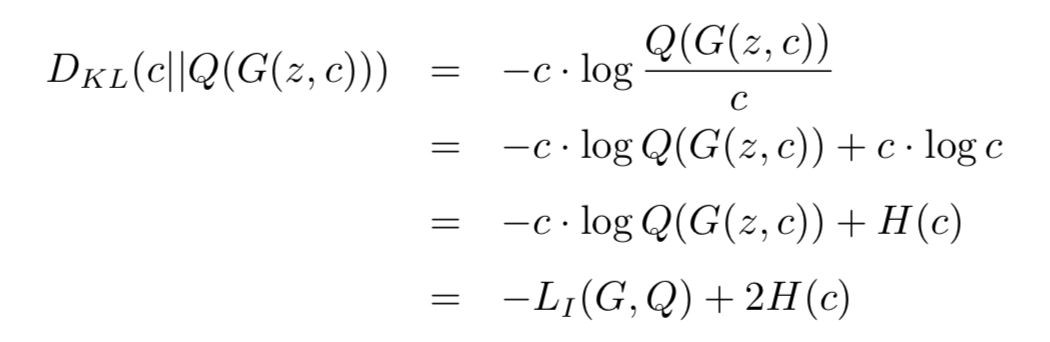
也就是說:

而 min DKL(c||Q(G(z, c))) 意味著減小 c 與 Q(G(z, c)) 的差別。

▲ 圖7. 普通GAN和InfoGAN的LI在訓練過程中的比較
如果我們不考慮 Q(x)σ 的影響,LI 的最佳化過程:

而 也意味著減小 c 與 Q(G(z, c))μ 的差。
也意味著減小 c 與 Q(G(z, c))μ 的差。
再縱觀整個模型,我們會發現這一對 LI 最佳化的過程,實質上是以 G 為編碼器(Encoder), Q 為解碼器(Decoder),生成的影象作為我們要編碼的碼(code),訓練一個自編碼器(Autoencoder),也就是說,作者口中的資訊理論最佳化問題,本質上是無監督訓練問題。
關於PaddlePaddle
在 PaddlePaddle 中,一個極為重要的概念即是 fluid.Program(),在官方檔案裡常見的 exe.run(program= fluid.default_startup_program())的 fluid.default_startup_program() 就是其中一個例子。
在這一使用中可以瞭解到,我們要用 exe.run() 中的 program 引數執行指定的 fluid.Program(),而官方檔案指出,當該引數未指定時,會執行 fluid.default_main_program(),而 fluid.default_main_program() 代表的是未指定 fluid.Program() 的所有操作。
註意,這裡說的是“所有”,由於 PaddlePaddle 沒有計算依賴檢測機制,即使在計算 fetch_list 中的值的時候不會用到操作也會被計算,這一點與 TensorFlow 極其不同,作者本人在使用過程中踩了很大的坑,還望各位註意。在執行多種任務的時候不要一股腦全部寫在 fluid.default_main_program() 之中, 這樣極其浪費資源,也容易造成一些問題。
一個新的 fluid.Program() 被建立之後,可以在 fluid.program_guard() 中指定該 fluid.Program() 中的操作與變數:
#建立Infer_program
Infer_program = fluid.Program()
#在這裡面定義Infer_program中的操作與變數
with fluid.program_guard(main_program = Infer_program):
#從外部透過feed傳入的變數,一般是輸入、標簽等
X = fluid.layers.data(name='X', shape=[X_dim], dtype='float32')
#全連結層
output = fluid.layers.fc(input = X, size = 128)
PaddlePaddle 中還需要註意的一點是,fluid.Variable 的名稱空間是全域性的,也就是說在同一或者不同 fluid. Program() 間,同名(fluid.Variable 的 name 屬性相同)的 fluid.Variable 所指向的變數是相同的,所以同一名稱在同一或者不同 fluid.Program () 中可以被使用多次,而不用擔心 TensorFlow 中會出現的 reuse 問題。
要對一個操作的中的權值的名稱進行定義(權值命名為 W1,偏置命名為 b1):
output = fluid.layers.fc(input = X,
size = 10,
param_attr = fluid.ParamAttr(name="W1"),
bias_attr = fluid.ParamAttr(name="b1"))
要在之後使用這些 fluid.Variable,例如在 Optimizer 中使用:
#可以直接用名稱指代對應的fluid.Variable
parameter_list = ["W1", "b1"]
#構建optimizer
optimizer = fluid.optimizer.AdamOptimizer()
#指定optimizer最佳化的標的和物件
optimizer.minimize(loss, parameter_list=parameter_list)
在構建完基本的運算操作後,便可以開始初始化操作了:
#初始化fluid.Executor(指定執行程式位置)
exe = fluid.Executor(fluid.CPUPlace())
#執行fluid.default_startup_program(),在fluid.program_guard()中
#若沒有指定初始化program,則預設為此program
exe.run(program=fluid.default_startup_program())
初始化完成後,可以開始訓練啦:
#在從外部傳入資料的時候要註意,傳入資料的資料型別必須與fluid.layers.data
#中定義的型別一致,否則會報錯
#如果傳入資料是list型別,建議轉換為np.array,否則可能回報錯:
#fedding的資料中包含lod資訊,請您轉換成lodtensor
#(渣翻譯, 原因是list被預設為含有變長資料)
feeding = {"X" : np.array(Z_noise).astype('float32')}
#傳入feeding中的資料,執行program程式,從計算結果中獲取loss
#(預設會被轉換成np.array,可在函式引數中設定)
loss_curr = exe.run(feed = feeding, program = program, fetch_list = [loss])
GAN實現
生成對抗網路(Generative Adversarial Nets)是一類新興的生成模型,由兩部分組成:一部分是判別模型(discriminator)D(·),用來判別輸入資料是真實資料還是生成出來的資料;另一部分是是生成模型(generator)G(·),由輸入的噪聲生成標的資料。GAN 的最佳化問題可以表示為:

其中 Pdata 是生成樣本,noise 是隨機噪聲。我們用一個雙層的 MLP 來演示:
#判別模型
def discriminator(x):
#使用fluid.unique_name.guard()新增模型內引數名稱的字首
with fluid.unique_name.guard('D_'):
D_h1 = fluid.layers.fc(input = x, size = 256, act = "relu")
D_logit = fluid.layers.fc(input = D_h1, size = 1, act = "sigmoid")
return D_logit
#生成模型
def generator(inputs):
with fluid.unique_name.guard('G_'):
D_h1 = fluid.layers.fc(input = inputs, size = 256, act = "relu")
D_logit = fluid.layers.fc(input = D_h1, size = 784, act = "sigmoid")
return D_logit
通常,一個 GAN 的訓練由兩部分組成,第一部分是對 D(·) 進行訓練,極大化標的函式:

第二部分是對 G(·) 進行訓練,極小化標的函式:
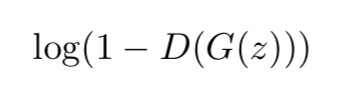
以下是兩部分最佳化的定義:
#參考Todd的LSGAN的實現,使用函式獲取模型所有變數
def get_params(program, prefix):
all_params = program.global_block().all_parameters()
return [t.name for t in all_params if t.name.startswith(prefix)]
#G最佳化程式
G_program = fluid.Program()
with fluid.program_guard(main_program = G_program):
#定義輸入資料
Z = fluid.layers.data(name='Z', shape=[Z_dim], dtype='float32')
#執行相關模型的計算
G_sample = generator(Z)
D_fake = discriminator(G_sample)
#計算損失函式
G_loss = 0.0 - fluid.layers.reduce_mean(fluid.layers.log(D_fake + 1e-8))
#定義optimizer最佳化的變數的範圍
theta_G = get_params(G_program, "G")
G_optimizer = fluid.optimizer.AdamOptimizer()
G_optimizer.minimize(G_loss, parameter_list=theta_G)
#D最佳化程式
D_program = fluid.Program()
with fluid.program_guard(main_program = D_program):
Z = fluid.layers.data(name='Z', shape=[Z_dim], dtype='float32')
X = fluid.layers.data(name='X', shape=[784], dtype='float32')
#在使用資料集時,要註意相應介面傳入資料的值的範圍
#paddle.dataset.mnist中的資料,範圍在[-1, 1]
#要將其轉換到sigmoid函式的值域內
X = X * 0.5 + 0.5
G_sample = generator(Z)
D_real = discriminator(X)
D_fake = discriminator(G_sample)
D_loss = 0.0 - fluid.layers.reduce_mean(fluid.layers.log(D_real + 1e-8)
+ fluid.layers.log(1.0 - D_fake + 1e-8))
theta_D = get_params(G_program, "D")
D_optimizer = fluid.optimizer.AdamOptimizer()
D_optimizer.minimize(D_loss, parameter_list=theta_D)
在定義好這些之後,是時候開訓練了:
#定義傳入的資料
feeding_withx= {"X" : np.array(X_mb).astype('float32'),
"Z" : np.array(Z_noise).astype('float32')}
feeding = {"Z" : np.array(Z_noise).astype('float32')}
#執行訓練操作並獲取當前損失函式的值
D_loss_curr = exe.run(feed = feeding_withx, program = D_program,
fetch_list = [D_loss])
G_loss_curr = exe.run(feed = feeding, program = G_program,
fetch_list = [G_loss])
若欲測試模型效果,可再定義一個 Inference:
#Inference
Infer_program = fluid.Program()
with fluid.program_guard(main_program = Infer_program):
Z = fluid.layers.data(name='Z', shape=[Z_dim], dtype='float32')
G_sample = generator(Z)
然後再這樣獲取 samples:
feeding = {"Z" : np.array(Z_noise).astype('float32')}
samples = exe.run(feed = feeding, program = Infer_program,
fetch_list = [G_sample])
後記
本文先前於今年 8 月完成,共享於 PaddlePaddle 論文復現群內,在 10 月 LSGAN 的復現公開之 後,參考該復現更改了模型引數命名和引數串列的實現方法,在此感謝 Todd 同學的復現對本文的幫助。

點選標題檢視更多論文解讀:
 #投 稿 通 道#
#投 稿 通 道#
讓你的論文被更多人看到
如何才能讓更多的優質內容以更短路徑到達讀者群體,縮短讀者尋找優質內容的成本呢? 答案就是:你不認識的人。
總有一些你不認識的人,知道你想知道的東西。PaperWeekly 或許可以成為一座橋梁,促使不同背景、不同方向的學者和學術靈感相互碰撞,迸發出更多的可能性。
PaperWeekly 鼓勵高校實驗室或個人,在我們的平臺上分享各類優質內容,可以是最新論文解讀,也可以是學習心得或技術乾貨。我們的目的只有一個,讓知識真正流動起來。
? 來稿標準:
• 稿件確系個人原創作品,來稿需註明作者個人資訊(姓名+學校/工作單位+學歷/職位+研究方向)
• 如果文章並非首發,請在投稿時提醒並附上所有已釋出連結
• PaperWeekly 預設每篇文章都是首發,均會新增“原創”標誌
? 投稿郵箱:
• 投稿郵箱:hr@paperweekly.site
• 所有文章配圖,請單獨在附件中傳送
• 請留下即時聯絡方式(微信或手機),以便我們在編輯釋出時和作者溝通
?
現在,在「知乎」也能找到我們了
進入知乎首頁搜尋「PaperWeekly」
點選「關註」訂閱我們的專欄吧
關於PaperWeekly
PaperWeekly 是一個推薦、解讀、討論、報道人工智慧前沿論文成果的學術平臺。如果你研究或從事 AI 領域,歡迎在公眾號後臺點選「交流群」,小助手將把你帶入 PaperWeekly 的交流群裡。

▽ 點選 | 閱讀原文 | 收藏復現程式碼
 知識星球
知識星球