人人都能看懂的機器學習！3個案例詳解聚類、回歸、分類演演算法-知識星球

導讀：機器是怎樣學習的，都學到了什麼？人類又是怎樣教會機器學習的？本文透過案例給你講清楚各類演演算法的原理和應用。

機器學習，一言以蔽之就是人類定義一定的計算機演演算法，讓計算機根據輸入的樣本和一些人類的幹預來總結和歸納其特徵和特點，並用這些特徵和特點和一定的學習標的形成對映關係，進而自動化地做出相應反應的過程。這個反應可能是做出相應的標記或判斷，也可能是輸出一段內容——圖片、程式程式碼、文字、聲音，而機器自己學到的內容我們可以描述為一個函式、一段程式、一組策略等相對複雜的關係描述。

演演算法這種東西在最初出現的時候是一種確定性的機器指令執行序列，也就是說，機器需要怎麼做早就在程式一開始就設定好。雖然說在程式執行的過程中可以依靠有限的引數對程式執行過程所涉及的物件，執行次數，執行分支條件等進行設定，但是基本行為邏輯已經大抵確定。

在這個過程中，機器——計算機是非常被動的，它老老實實地嚴格執行程式員賦予它們的指令執行序列，沒有任何“學習”的行為。這也沒辦法，因為最開始的圖靈機模型在設計的時候就是期望計算機以這種方式。

機器學習從學習的種類來說，最常見的我們習慣分作兩種，一種叫“無監督學習”（Unsupervised Learning），一種叫“有監督學習”（Supervised Learning）。

所謂“無監督學習”，是指人們在獲得訓練的向量資料後在沒有標簽的情況下嘗試找出其內部蘊含關係的一種挖掘工作，這個過程中使用者除了可能要設定一些必要的“超引數”（Hyper-parameter）以外不用對這些樣本做任何的標記甚至是過程幹預；“有監督學習”與此不同，每一個樣本都有著明確的標簽，最後我們只是要總結出這些訓練樣本向量與標簽的對映關係。

所以這在這兩種方式下，處理的邏輯有很大的區別，對於初學的朋友需要格外註意。

01 聚類

聚類——英文為Clustering，它就是我們說的典型的“無監督學習”的一種，就是把物理物件或抽象物件的集合分組為由彼此類似的物件組成的多個類的分析過程。

聚類這種行為我們不要覺得很神秘，也不要覺得這個東西是機器學習所獨有的，恰恰相反，聚類的行為本源還是人自身。我們學習的所有的資料挖掘或者機器學習的演演算法或者思想的來源都是人類自己的思考方式，只不過我們把它教給機器讓它們代勞，讓他們成為我們肢體和能力的延伸而不是讓他們替我們做創造和思考。

聚類是一種什麼現象呢？我們人類在認識客觀世界的過程中其實一直遇到容量性的問題，我們遇到的每一棵樹、每一朵花、每一隻昆蟲、每一頭動物、每一個人、每一棟建築……每個個體之間其實都不同，有的差距還相當大。那麼我們人在認知和記憶這些客觀事物的過程中就會異常痛苦，因為量實在是大到無法承受的地步。

因此人類才會在“自底向上”的認識世界的過程中“偷懶”性地選擇了歸納歸類的方式，註意“偷懶”的這種方式是人類與生俱來的方法。

我們在小時候被父母用看圖說話的方式來教咿呀學語的時候就有過類似的體會了，圖片上畫了一隻猴子，於是我們就認識了，這是一隻猴子；圖片上畫了一輛汽車，於是我們就瞭解了，這是一輛汽車……

等我們上街或者去動物園的時候再看，猴子也不是畫上的猴子，而且眾多猴子之間也長得各式各樣，每個都不同，我們會把它們當成一個一個的新事物去認識嗎？我們看汽車也同樣，大小，顏色，樣式，甚至是喇叭的聲音也是形形色色五花八門，它們在我們眼裡是一個個新的事物嗎？不，它們都還是汽車。

這些事物之間確實有所不同，但是它們對我們的認知帶來了很大的困擾嗎？並沒有。我們無論如何是不會把猴子和汽車當成一類事物去認知的，猴子彼此之間是不同，但是體格、毛髮、行為舉止，種種形態讓我們認為這些不同種類的猴子都還是猴子一個大類的動物，別說是和汽車混為一談，就是跟狗、馬匹、熊這些脊椎動物我們也能輕易地分開。

人類天生具備這種歸納和總結的能力，能夠把認知的事物相似地放到一起來作為一類事物做認識，它們之間可以有彼此的不同，但是有一個我們心裡的“限度”，只要在這個限度內，特徵稍有區別無關大礙，它們仍然還是這一類事物。

在這一類事物的內部，同樣有這種現象，一部分個體之間比較相近，而另一部分個體之間比較相近，這兩部分個體彼此之間我們人還是能夠明顯認知到差別，那麼這個部分的事物又會在大類別的內部重新劃分成兩個不同的部分進行認知。比如汽車直觀從樣子上可以分成小轎車、卡車、麵包車等種類，蟲子們也被人輕易地從外型上區別為飛蟲、爬蟲、毛毛蟲……

在沒有人特意教給我們不同小種群的稱謂與特性之前，我們自然具備的這種由我們主觀的認知能力，以特徵形態的相同或近似將它們劃在一個概念下，特徵形態的不同劃在不同的概念下，這本身就是聚類的思維方式。

比較常用的聚類演演算法有K-Means、DBSCAN等幾種，基本思路都是利用每個向量之間的“距離”——這裡指的是空間中的歐氏距離或者曼哈頓距離。從遠近來進行彼此是否更適於從屬與同一類別來做的分類判斷。

假如有三個1維樣本，一個180，一個179，一個150，這三個向量如果要分成兩類的話，應該是180和179這兩個分在一個類別，150單一個類別。原因就是180和179兩個的距離為1，而180和179距離150分別為30和29個單位——非常遠，就是從肉眼感官上來看也是這樣。用機器來做學習的話，它也能夠透過演演算法自動去感知到這些向量之間的距離，然後將它們彼此之間那些靠得近的分在一起以區別於其他類簇。

在用機器做聚類學習的時候，我們每種演演算法都對應有相應的計算原則，可以把輸入的各種看上去彼此“相近”的向量分在一個群組中。然後下一步，人們通常更有針對性地去研究每一組聚在一起的物件所擁有的共性以及那些遠離各個群組的孤立點——這種孤立點研究在刑偵、特殊疾病排查等方面都有應用。

在這個過程中，從獲得到具體的樣本向量，到得出聚類結果，人們是不用進行幹預的，這就是“非監督”一詞的由來。

02 回歸

回歸是一種解題方法，或者說“學習”方法，也是機器學習中一塊比較重要的概念。

回歸的英文是Regression，單詞原型的regress大概的意思是“回退，退化，倒退。”其實Regression——回歸分析的意思是借用裡面“倒退，倒推”的含義。簡單說就是“由果索因”的過程，是一種歸納的思想——當我看到大量的事實所呈現的樣態，我推斷出原因或客觀蘊含的關係是如何的；當我看到大量的觀測而來的向量（數字）是某種樣態，我設計一種假說來描述出它們之間蘊含的關係是如何的。

在機器學習領域，最常用的回歸是兩大類——一類是線性回歸，一類是非線性回歸。

所謂線性回歸，就是在觀察和歸納樣本的過程中認為向量和最終的函式值呈現線性的關係。而後設計這種關係為：

y = f(x) = wx + b

這裡的w和x分別是1×n和n×1的矩陣，wb則指的是這兩個矩陣的內積。具象一點說，例如，如果你在一個實驗中觀察到一名病患的幾個指標呈現線性關係（註意這個是大前提，如果你觀察到的不是線性關係而用線性模型來建模的話，是會得到欠擬合的結果的）。

拿到的x是一個5維的向量，分別代表一名患者的年齡、身高、體重、血壓、血脂這幾個指標值，y標簽是描述他們血糖程度的指標值，x和y都是觀測到的值。在拿到大量樣本（就是大量的x和y）後，我猜測向量 (年齡,身高,體重,血壓,血脂) 和與其有關聯關係的血糖程度y值有這樣的關係：

y=w₁×年齡+w₂×身高+w₃×體重+w₄×血壓+w₅×血脂+b

那麼就把每一名患者的 (年齡,身高,體重,血壓,血脂) 具體向量值帶入，並把其血糖程度y值也帶入。這樣一來，在所有的患者資料輸入後，會出現一系列的六元一次方程，未知數是w₁~w₅和b——也就是w矩陣的內容和偏置b的內容。而下麵要做的事情就是要把w矩陣的內容和偏置b的內容求出一個最“合適”的解來。這個“合適”的概念就是要得到一個全域性範圍內由f(x)對映得到的y和我真實觀測到的那個y的差距的加和，寫出來是這種方式：

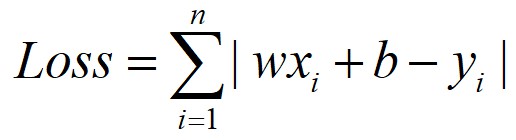
怎麼理解這個Loss的含義呢？右面的表示加和，相當於做一個一個迴圈，i是迴圈變數，從1做到n，改寫訓練集當中的每一個樣本向量。加和的內容是wx_i+b和y_i的差值，每一個訓練向量x_i在透過我們剛剛假設的關係f(x)=wx+b對映後與實際觀測值y_i的差距值。取絕對值的含義就是指這個差距不論是比觀測值大或者觀測值小，都是一樣的差距。將全域性範圍內這n個差距值都加起來我們管他叫總差距值好了，就是這個的含義。

那麼顯而易見，這個對映關係中如果w和b給的理想的話，應該這個差距值是0，因為每個x經過對映都“嚴絲合縫”地和觀測值一致了——這種狀況太理想了，在實際應用中是見不到的。不過，Loss越小就說明這個對映關係描述越精確，這個還是很直觀的。那麼想辦法把Loss描述成：

Loss=f(w, b)

再使用相應的方法找出保證Loss盡可能小的w和b的取值，就算是大功告成了。我們後面會講計算機怎麼來求這一類的解——放心，有辦法的，即便不用聯立解方程。一旦得到一個誤差足夠小的w和b並能夠在驗證用的資料集上有滿足當前需求的精度表現後就可以了。例如，預測病患的血糖誤差為誤差平均小於等於0.3為容忍上線，訓練後在驗證集上的表現為誤差平均為0.2，那就算是合格了。

請註意，在傳統的機器學習中回歸、分類這些演演算法裡都有一個要把獲取到的資料集分成訓練集合驗證集的過程。用訓練集資料來做訓練，歸納關係用；用驗證集資料來做驗證，避免過擬合現象，如果你不太明白過擬合是什麼意思也沒關係後面我們會講的，不必著急。資料集的劃分三七開也可以，二八開也沒什麼不行，現在生產環境中大致用的都是這樣一種比例，反正訓練集一側用資料多的那部分。

由於這種假設中輸入的x向量與標簽值y是一種線性關係y=f(x)=wx+b，所以才叫做線性回歸。最常見的形式是y=f(x)=ax+b這種形式，也就是x是一個一維向量，w也是一個一維向量的情況。如果是呈現其他關係比如指數關係，對數關係，那麼這種時候你用線性回歸去做擬合會發現它的損失函式非常大，在驗證集上表現出來的誤差也非常大，這是一種欠擬合現象，我們後面同樣會講，大家先技術這樣一個名詞。

非線性回歸之中在機器學習領域應用最多的當屬邏輯回歸。它和線性回歸都叫回歸，但是邏輯回歸看上去更像分類。我們先在回歸這一節提一下這種回歸的工作方式。與前面我們說的線性回歸不同，在這種模型中觀察者假設的前提是y只有兩種值，一種是1，一種是0，或者說“是”或“否”的這種判斷。

這裡面的wx+b和前麵線性回歸中所說的wx+b是一個概念，都是指一個w矩陣和x做了內積再和偏置b做了一個加和。如果設z=wx+b那麼這個回歸的分類模型運算式就可以改寫為：

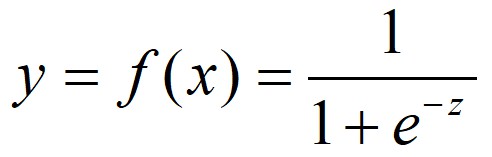
函式影象為：

橫軸是z，縱軸是y，一個多維的x經過這樣兩次對映後最後投射在y上是一個取值只有1和0二項分佈。也就是我們前面說的產生了一個“是”或“否”的分類。

訓練的過程跟普通線性回歸也是一樣的，只不過損失函式的形式不同。但是，它的損失函式的含義仍舊是表示這種擬合殘差與待定繫數的關係，並透過相應的手段進行迭代式的最佳化，最後透過逐步調整待定繫數減小殘差。邏輯回歸的運算式的定義本源是來自於伯努利分佈的，後面我們也會有相對詳細的說明，這裡先做一個感性認識。

03 分類

分類是我們在利用機器學習中使用的最多的一大類演演算法，我們通常也喜歡把分類演演算法叫“分類器”。

這個說法其實也非常形象，在我們看來，這就是一個黑盒子，有個入口，有個出口。我們在入口丟進去一個“樣本”，在出口期望得到一個分類的“標簽”。

比如，一個分類器可以進行圖片內容的分類標簽，我們在“入口”丟進去一張老虎的照片，在“出口”得到“老虎”這樣一個描述標簽；而當我們在“入口”丟進去一張飛機的照片，在“出口”得到“飛機”這樣一個描述標簽，這就是一個分類器最為基本的分類工作過程。

一個分類器模型在它誕生（初始化）的時候其實是不具備這種功能的，而要讓它具備這種功能只有透過給予它大量的圖片以及圖片所對應的標簽分類，讓它自己進行充分地總結和歸納，才能具備這樣一種能力。

在剛剛看到的邏輯回歸這種方式中我們已然看到了一些端倪。邏輯回歸和普通的線性回歸不同，它的擬合是一種非線性的方式。而最終輸出“標簽值”雖然是一種實數變數，而最終分類的結果卻期望是一種確定的值“是”（1）或“不是”（0）。其他各種分類器的輸出通常也是離散的變數，體現出來也多是非線性的分類特點。

我們在編寫程式碼教會分類器怎麼做學習的時候，其實是在教它如何建立一種輸入到輸出的對映邏輯，以及讓它自己調整這種邏輯關係，使得邏輯更為合理。

而合理與否的判斷也非常明確，那就是召回率和精確率兩個指標——召回率指的是檢索出的相關樣本和樣本庫（待測物件庫）中所有的相關樣本的比率，衡量的是分類器的查全率。精確率是檢索出的相關樣本數與檢索出的樣本總數的比率，衡量的是分類器的查準率。

具體來說，譬如有一個1000個樣本的訓練集，是1000張照片，裡面有200張是貓，200張是狗，600張是兔子，一共分成三類。我們將每個照片向量化後，加上它的標簽

“貓”——“0”
“狗”——“1”
“兔子”——“2”

這相當於一個x和y的對應關係，把它們輸入到訓練集去訓練（但是這個地方的標簽0、1、2並不是實數定義，而是離散化的標簽定義，通常習慣用one-hot獨熱編碼的方式來表示）。經過多輪訓練之後，分類器將邏輯關係調整到了一個相對穩定的程度，然後用這個分類器再對這200張貓，200張狗，600張兔子進行分類的時候。發現：

200張貓的圖片中，有180張可以正確識別為貓，而有20張誤判為狗。

200張狗的圖片可以全部判斷正確為狗。

600張兔子的圖片中，有550張可以正確識別為兔子，還有30張被誤判為貓，20張誤判為狗。

你可不要覺得奇怪，在所有的機器學習或者深度學習訓練的工程中，誤判率幾乎是沒有辦法消滅的，只能用盡可能科學的手段將誤判率降低。不要太難為機器，其實人都沒辦法保證所有的資訊100%正確判斷，尤其是在圖片大小、圖片清晰程度、光線明暗懸殊的情況下，不是嗎？那就更別說機器了，它更做不到。

我們還是來解釋召回率和精確率的問題，就剛才這個例子來說，一共1000張圖片中，200張是貓，但是隻能正確識別出180張，所以貓的召回率是180÷200=90%，600張兔子中正確識別550張，所以兔子的召回率是550÷600≈91.7%，就這樣計算。

而在1000中圖片中，當我檢索狗的時候會檢索出240張狗的圖片，其中有200張確實是狗，有20張是被誤判的貓，還有20張是被誤判的兔子，所以240張狗的圖片中正確的僅有200張而已，那麼狗的精確率為200÷240≈83.3%。怎麼樣，這兩個概念不難理解吧。

分類的訓練過程和回歸的訓練過程一樣，都是極為套路化的程式。

第一，輸入樣本和分類標簽。
第二，建立對映假說的某個y=f(x)的模型。
第三，求解出全域性的損失函式Loss和待定繫數w的對映關係，Loss=g(w)。
第四，透過迭代最佳化逐步降低Loss，最終找到一個w能滿足召回率和精確率滿足當前場景需要。註意這說的尤其指的是在驗證資料集上的表現。

大家請註意這4個步驟，我們從前面最簡單的機器學習的例子中已經總結出來一個最為有概括性的科學性流程。這種流程廣泛使用，並且在其它機器學習的場景中也是可以順利落地的。

分類器的訓練和工作過程就是這個樣子了，聽起來分類器的工作過程非常簡單，但是要知道人的智慧行為其實就是一種非常精妙或者稱為完美的分類器。他能夠處理極為複雜，極為抽象的輸入內容——不管是文字、聲音、影象，甚至是冷、熱、刺痛感、瘙癢感這種難以名狀的刺激，並且能夠在相當短的時間內進行合理的輸出——例如對答、附和、評論，亦或是尖叫、大笑等各種喜怒哀樂的反應與表現。從定義的角度上來說，人其實就是一種極為複雜的且極為智慧的分類器。而我們在工業上使用的分類器則通常是非常片面的，偏門的，只研究一種或幾個事物的“專業性”的分類器，這和我們人類的分類能力區別就太大了。

04 綜合應用

到現在為止，我們看到的絕大多數的機器學習的應用環境都非常單純——向量清洗到位，邊界劃定清晰。

例如，垃圾郵件的分揀，能夠透過郵件內容的輸入來判斷郵件是否為垃圾郵件；新聞的自動分類，能夠透過欣慰內容的分類來判斷新聞的類別或描述內容的屬性；攝像頭對車牌號的OCR電子識別手寫識別，這些應用可以透過輸入一個影象來得到其中蘊含的文字資訊向量，諸如此類等等，這些都是早些年應用比較成熟的領域，在這種應用場景中機器透過學習能夠取代一些純粹的體力勞動。

在近幾年，隨著計算機能力的提升，尤其是GPU平行計算的普及化，使得很多原來高密度計算的場景變得門檻越來越低，人們在商用領域已經開始尋找用深度學習的網路來做一些原來不可想象的事情。

例如這種使用摺積神經網路對照片進行風格處理，拿一張輸入的普通照片，再拿一張有著較強藝術風格的繪畫作品，然後透過摺積網路進行處理，最後由計算機“創作”出一幅內容基於照片但是風格基於繪畫作品的新作出來。而這種事情在幾年前是難以想象的，因為這看上去太“智慧”了，太有“創造力”了。

還有類似這種，我們輸入一張照片，然後讓計算機根據這張照片的風格和內容，憑空創造一張很像但不一樣的照片出來。註意哦，這個跟Photoshop的功能可是完全不同的，它是全自動。在這些圖中，右側的圖都是源圖，左側的圖都是計算機生成的圖，有水波紋、雲朵、花叢、還有隨意的藝術塗鴉。怎麼樣，有不少真的是可以以假亂真了吧。這都是使用深度神經網路處理的結果。