每個資料科學專家都應該知道的六個機率分佈

01 介紹

假設你是一所大學的老師。在對一週的作業進行了檢查之後，你給所有的學生打了分數。你把這些打了分數的論文交給大學的資料錄入人員，並告訴他建立一個包含所有學生成績的電子錶格。但這個人卻只儲存了成績，而沒有包含對應的學生。

他又犯了另一個錯誤，在匆忙中跳過了幾項，但我們卻不知道丟了誰的成績。我們來看看如何來解決這個問題吧。

一種方法是將成績視覺化，看看是否可以在資料中找到某種趨勢。

上面展示的圖形稱為資料的頻率分佈。其中有一個平滑的曲線，但你註意到有一個異常情況了嗎？在某個特定的分數範圍內，資料的頻率異常低。所以，最準確的猜測就是丟失值了，從而導致在分佈中出現了凹陷。

這個過程展示了你該如何使用資料分析來嘗試解決現實生活中的問題。對於任何一位資料科學家、學生或從業者來說，分佈是必須要知道的概念，它為分析和推理統計提供了基礎。

雖然機率為我們提供了數學上的計算，而分佈卻可以幫助我們把內部發生的事情視覺化。

在本文中，我將介紹一些重要的機率分佈，並會清晰全面地對它們進行解釋。

註意：本文假設你已經具有了機率方面的基本知識。如果沒有，可以參考這篇有關機率基礎的文章。

02 常見的資料型別

在開始詳細講述分佈之前，先來看看我們會遇到哪些種類的資料。資料可以分為離散的和連續的。

離散資料：顧名思義，只包含指定的值。例如，當你投骰子的時候，輸出結果只可能是1、2、3、4、5或6，而不可能出現1.5或2.45。

連續資料：可以在給定的範圍內取任何值。範圍可以是有限的，也可以是無限的。例如，女孩的體重或身高、路程的長度。女孩的體重可以是54千克、54.5千克，或54.5436千克。

現在我們開始學習分佈的型別。

03 分佈的型別

伯努利分佈

我們首先從最簡單的分佈伯努利分佈開始。

伯努利分佈只有兩種可能的結果，1（成功）和0（失敗）。因此，具有伯努利分佈的隨機變數X可以取值為1，也就是成功的機率，可以用p來表示，也可以取值為0，即失敗的機率，用q或1-p來表示。

機率質量函式由下式給出：px(1-p)1-x， 其中x € (0, 1)。它也可以寫成：

成功與失敗的機率不一定相等。這裡，成功的機率（p）與失敗的機率不同。所以，下圖顯示了我們之間比賽結果的伯努利分佈。

這裡，成功的機率 = 0.15，失敗的機率 = 0.85 。如果我打了你，我可能會期待你向我打回來。任何分佈的基本預期值是分佈的平均值。來自伯努利分佈的隨機變數X的期望值如為：

E(X) = 1*p + 0*(1-p) = p

隨機變數與二項分佈的方差為：

V(X) = E(X²) – [E(X)]² = p – p² = p(1-p)

伯努利分佈的例子有很多，比如說明天是否要下雨，如果下雨則表示成功，如果不下雨，則表示失敗。

均勻分佈

對於投骰子來說，結果是1到6。得到任何一個結果的機率是相等的，這就是均勻分佈的基礎。與伯努利分佈不同，均勻分佈的所有可能結果的n個數也是相等的。

如果變數X是均勻分佈的，則密度函式可以表示為：

均勻分佈的曲線是這樣的：

你可以看到，均勻分佈曲線的形狀是一個矩形，這也是均勻分佈又稱為矩形分佈的原因。其中，a和b是引數。

花店每天銷售的花束數量是均勻分佈的，最多為40，最少為10。我們來計算一下日銷售量在15到30之間的機率。

日銷售量在15到30之間的機率為(30-15)*(1/(40-10)) = 0.5

同樣地，日銷售量大於20的機率為 = 0.667

遵循均勻分佈的X的平均值和方差為：

平均值 -> E(X) = (a+b)/2

方差 -> V(X) =  (b-a)²/12

標準均勻密度的引數 a = 0 和 b = 1，因此標準均勻密度由下式給出：

二項分佈

讓我們來看看玩板球這個例子。假設你今天贏了一場比賽，這表示一個成功的事件。你再比了一場，但你輸了。如果你今天贏了一場比賽，但這並不表示你明天肯定會贏。我們來分配一個隨機變數X，用於表示贏得的次數。 X可能的值是多少呢？它可以是任意值，這取決於你擲硬幣的次數。

只有兩種可能的結果，成功和失敗。因此，成功的機率 = 0.5，失敗的機率可以很容易地計算得到：q = p – 1 = 0.5。

二項式分佈就是隻有兩個可能結果的分佈，比如成功或失敗、得到或者丟失、贏或敗，每一次嘗試成功和失敗的機率相等。

結果有可能不一定相等。如果在實驗中成功的機率為0.2，則失敗的機率可以很容易地計算得到 q = 1 – 0.2 = 0.8。

每一次嘗試都是獨立的，因為前一次投擲的結果不能決定或影響當前投擲的結果。只有兩個可能的結果並且重覆n次的實驗叫做二項式。二項分佈的引數是n和p，其中n是試驗的總數，p是每次試驗成功的機率。

在上述說明的基礎上，二項式分佈的屬性包括：

1. 每個試驗都是獨立的。

2. 在試驗中只有兩個可能的結果：成功或失敗。

3. 總共進行了n次相同的試驗。

4. 所有試驗成功和失敗的機率是相同的。 （試驗是一樣的）

二項分佈的數學表示由下式給出：

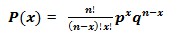
成功機率不等於失敗機率的二項分佈圖：

現在，當成功的機率 = 失敗的機率時，二項分佈圖如下

二項分佈的均值和方差由下式給出：

平均值 -> µ = n*p

方差 -> Var(X) = n*p*q

正態分佈

正態分佈代表了宇宙中大多數情況的運轉狀態。大量的隨機變數被證明是正態分佈的。任何一個分佈只要具有以下特徵，則可以稱為正態分佈：

1. 分佈的平均值、中位數和樣式一致。

2. 分佈曲線是鐘形的，關於線 x = μ 對稱。

3. 曲線下的總面積為1。

4. 有一半的值在中心的左邊，另一半在右邊。

正態分佈與二項分佈有著很大的不同。然而，如果試驗次數接近於無窮大，則它們的形狀會變得十分相似。

遵循正態分佈的隨機變數X的值由下式給出：

正態分佈的隨機變數X的均值和方差由下式給出：

均值 -> E(X) = µ

方差 -> Var(X) = σ^2

其中，μ（平均）和σ（標準偏差）是引數。

隨機變數X〜N（μ，σ）的圖如下所示。

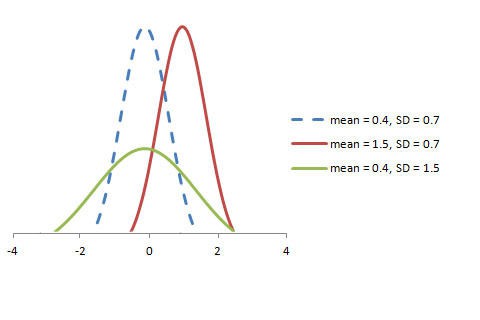
標準正態分佈定義為平均值等於0，標準偏差等於1的分佈：

泊松分佈

假設你在一個呼叫中心工作，一天裡你大概會接到多少個電話？它可以是任何一個數字。現在，呼叫中心一天的呼叫總數可以用泊松分佈來建模。這裡有一些例子：

1. 醫院在一天內錄製的緊急電話的數量。

2. 某個地區在一天內報告的失竊的數量。

3. 在一小時內抵達沙龍的客戶人數。

4. 在特定城市上報的自殺人數。

5. 書中每一頁列印錯誤的數量。

泊松分佈適用於在隨機時間和空間上發生事件的情況，其中，我們只關註事件發生的次數。

當以下假設有效時，則稱為**泊松分佈**

1. 任何一個成功的事件都不應該影響另一個成功的事件。

2. 在短時間內成功的機率必須等於在更長的間內成功的機率。

3. 時間間隔變小時，在給間隔時間內成功的機率趨向於零。

泊松分佈中使用了這些符號：

• λ是事件發生的速率

• t是時間間隔的長

• X是該時間間隔內的事件數。

其中，X稱為泊松隨機變數，X的機率分佈稱為泊松分佈。

令μ表示長度為t的間隔中的平均事件數。那麼，µ = λ*t。

泊松分佈的X由下式給出：

平均值μ是該分佈的引數。 μ也定義為該間隔的λ倍長度。泊松分佈圖如下所示：

下圖顯示了隨著平均值的增加曲線的偏移情況：

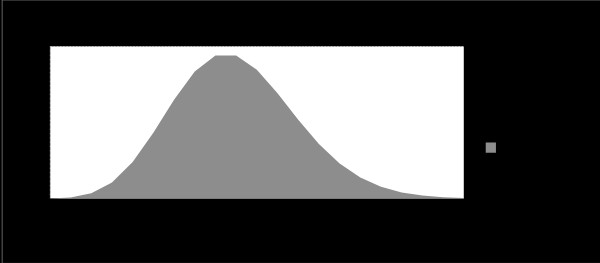
可以看出，隨著平均值的增加，曲線向右移動。

泊松分佈中X的均值和方差：

均值 -> E(X) = µ
方差 -> Var(X) = µ

指數分佈

讓我們再一次看看呼叫中心的那個例子。不同呼叫之間的時間間隔是多少呢？在這裡，指數分佈模擬了呼叫之間的時間間隔。

其他類似的例子有：

1. 地鐵到達時間間隔

2. 到達加油站的時間

3. 空調的壽命

指數分佈廣泛用於生存分析。從機器的預期壽命到人類的預期壽命，指數分佈都能成功地提供結果。

具有**的指數分佈**的隨機變數X：

f(x) = { λe-λx,  x ≥ 0

引數 λ>0 也稱為速率。

對於生存分析，λ被稱為任何時刻t的裝置的故障率，假定它已經存活到t時刻。

遵循指數分佈的隨機變數X的均值和方差為：

平均值 -> E(X) = 1/λ

方差 -> Var(X) = (1/λ)²

此外，速率越大，曲線下降越快，速率越慢，曲線越平坦。下麵的圖很好地解釋了這一點。

為了簡化計算，下麵給出一些公式。

P{X≤x} = 1 – e-λx 對應於x左側曲線下的面積。

PP{X>x} = e-λx 對應於x右側曲線下的面積。

P{x1-λx1 – e-λx2, corresponds to the area under the density curve between x1 and x2.

P{x1-λx1 – e-λx2 對應於x1和x2之間地曲線下的面積。

04 各種分佈之間的關係

伯努利與二項分佈之間的關係

1. 伯努利分佈是具有單項試驗的二項式分佈的特殊情況。
2. 伯努利分佈和二項式分佈只有兩種可能的結果，即成功與失敗。
3. 伯努利分佈和

二項式分佈都具有獨立的軌跡。

泊松與二項式分佈之間的關係

泊松分佈在滿足以下條件的情況下是二項式分佈的極限情況：

1. 試驗次數無限大或n → ∞。

2. 每個試驗成功的機率是相同的，無限小的，或p → 0。

3. np = λ，是有限的。

正態分佈關係

正態分佈是在滿足以下條件的情況下二項分佈的另一種限制形式：

1. 試驗次數無限大，n → ∞。

2. p和q都不是無限小。

正態分佈也是引數λ → ∞的泊松分佈的極限情況。

指數和泊松分佈之間的關係

如果隨機事件之間的時間遵循速率為λ的指數分佈，則時間長度t內的事件總數遵循具有引數λt的泊松分佈。

05 結束語

機率分佈在許多領域都很常見，包括保險、物理、工程、電腦科學甚至社會科學，如心理學和醫學。它易於應用，並應用很廣泛。本文重點介紹了日常生活中經常能遇到的六個重要分佈，並解釋了它們的應用。現在，你已經能夠識別、關聯和區分這些分佈了。

來源：雲棲社群

精彩活動

福利 · 閱讀 | 免費申請讀大資料新書 第23期

推薦閱讀

2017年資料視覺化的七大趨勢！ 

全球100款大資料工具彙總（前50款） 

論大資料的十大侷限

大資料時代的10個重大變革

大資料七大趨勢 第一個趨勢是物聯網

Q: 說說你對機率分佈的認識？

歡迎留言與大家分享

請把這篇文章分享給你的朋友

轉載 / 投稿請聯絡：hzzy@hzbook.com

更多精彩文章，請在公眾號後臺點選“歷史文章”檢視